4.3 Порядок выполнения работы

4.3.1 Открыть архив, созданный в лабораторной работе №3, в пакете программ Microsoft Office Excel. Привести документ к виду, представленному на рис. 4.2.

Рис. 4.2 Документ Microsoft Excel. Зависимость температуры печи от времени

4.3.2 Открыть изменённый архив в Matlab, выполнив File/Open. В открывшемся окне (см. рис. 4.3) выбрать Next/Finish.

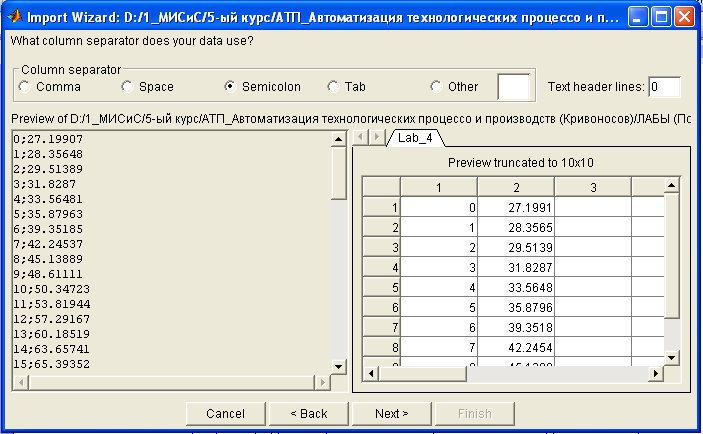
Рис. 4.3 Зависимость температуры печи от времени в Matlab

4.3.3 В Matlab запустить Simulink, нажав в панели инструментов на пиктограмму . Создать новый документ, выполнив File/New/Model. Собрать схему, приведённую на рис. 4.4. В блок From Workspace в поле Data вести имя архива “Lab_4”. Запустить проект, нажав на панель инструментов на кнопку Start Simulation . Открыв Scope, проанализировать график переходного процесса (см. рис. 4.5).

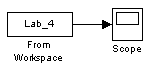
Рис. 4.4 Схема для построения графика переходного процесса

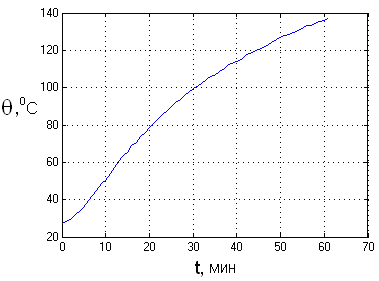
Рис. 4.5 График переходного процесса

4.3.4 Для идентификации объекта собрать схему, изображенную на рис. 4.6. Здесь Δx – сигнал управления в %, θ₀ – начальное значение температуры, ^оС. Для схемы установить дискретность моделируемого времени равную дискретности съема данных при получении переходной характеристики (Вкладка Simulation → Simulation parameters → Solver option → Fixed step + Ode 5 (в соседнем меню)). Далее в Matlab в окне Command Window ввести значения параметров K, T1 и T2 (см. рис. 4.7). После этого открыть блок NCD Outport, выбрать в меню Optimization/Parameteres, в появившемся окне (см. рис. 4.8) ввести оптимизируемые параметры, их нижние и верхние пределы оптимизации. Запустить проект, нажав на панель инструментов на кнопку Start (см. рис. 4.9). Далее в Matlab в окне Command Window просмотреть значения параметров K, T1 и T2 (см. рис. 4.10).

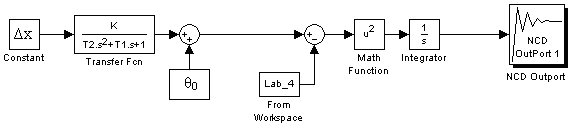
Рис. 4.6 Схема для идентификации объекта

Рис. 4.7 Ввод параметров K, T1 и T2

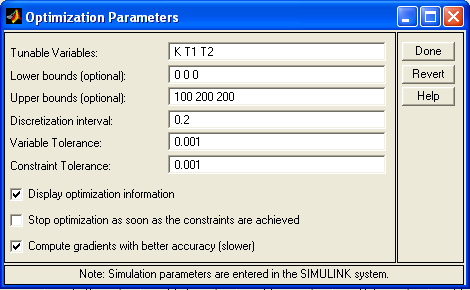
Рис. 4.8 Определение параметров оптимизации К, Т1, Т2

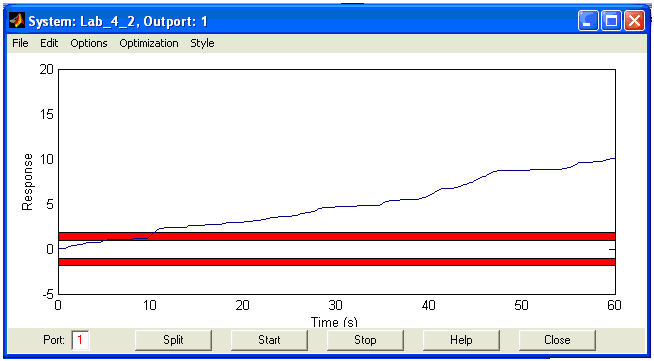
Рис. 4.9 Результат работы блока NCD Outport

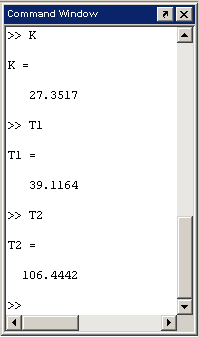
Рис. 4.10 Просмотр оптимизированных параметров К, Т1, Т2

4.3.5 Используя Scope, просмотреть графики переходного процесса, построенных по измеренным (в лабораторной работе №3) и по модельным значениям (см. рис. 4.11). Проанализировать полученные результаты (см. рис. 4.12).

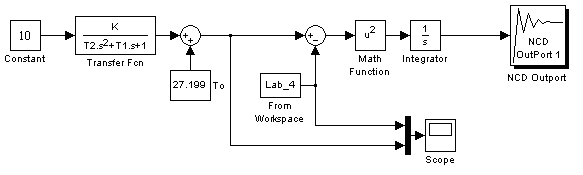
Рис. 4.11 Схема для просмотра графиков переходного процесса, построенных по измеренным и по модельным значениям

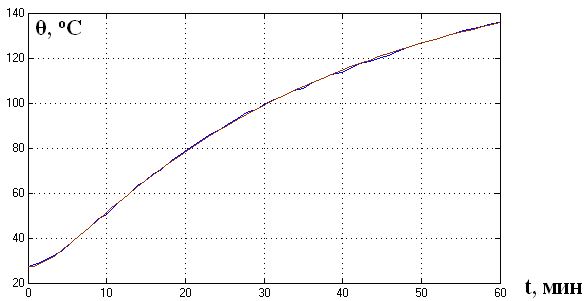
Рис. 4.12 Графики переходного процесса, построенные по измеренным и по модельным значениям

6. Сделать выводы по проделанной работе.

4.4 Контрольные вопросы и задания

4.4.1 Что называется идентификацией объекта?

4.4.2 Каким образом определяется время запаздывания?

4.4.3 Какой вид имеет переходная характеристика апериодического звена 2-го порядка?

4.4.4 Какие величины можно определить по переходной характеристике апериодического звена 2-го порядка?

Обязательные составляющие отчета

1. Переходная характеристика объекта управления.

2. Текст программы или схема оптимизации.

3. График сравнения экспериментальной и модельной переходных функций объекта управления.

Лабораторная работа №5

Определение оптимальных параметров ПИ регулятора

5.1 Цель работы: Ознакомление с особенностями реализации ПИ закона регулирования контроллера. Изучение способов оптимизации коэффициентов регулятора.

5.2 Теоретическое введение

ПИД регулятор контроллера выполняет пропорционально-итегрально-дифференциальное преобразование сигнала и описывается следующей переходной характеристикой:

,

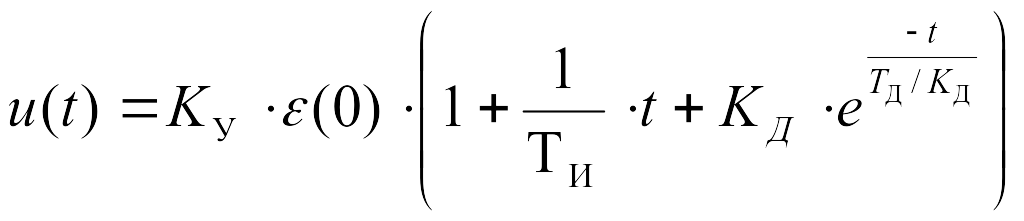где u(t) – управляющая переменная в автоматическом режиме регулятора;

ε(0) – ступенчатое изменение нормализованного сигнала ошибки;

К_У – усилие регулятора;

Т_И – постоянная времени интегрирования;

Т_Д – время дифференцирования;

К_Д – коэффициент дифференцирования.

Рассматривается задача оптимизации коэффициентов ПИ закона регулирования. Существует много способов решения данной задачи. Например, можно воспользоваться пакетами Siam, Matlab. А также можно применить метод структурного моделирования в комплексе с оптимизацией функционала качества по методу наименьших квадратов.

Оптимизация коэффициентов ПИ регулятора проводится согласно схеме, представленной на рис. 5.1.

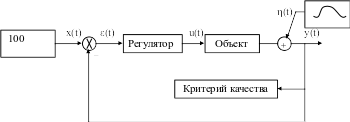
Рис. 5.1 Схема оптимизации параметров ПИ регулятора

На рис. 5.1: x(t) – сигнал задания;

ε(t) – сигнал ошибки;

u(t) – сигнал управления;

η(t) – помеха измерения;

y(t) – выход объекта.

При использовании пакета Siam критерий качества выглядит следующим образом:

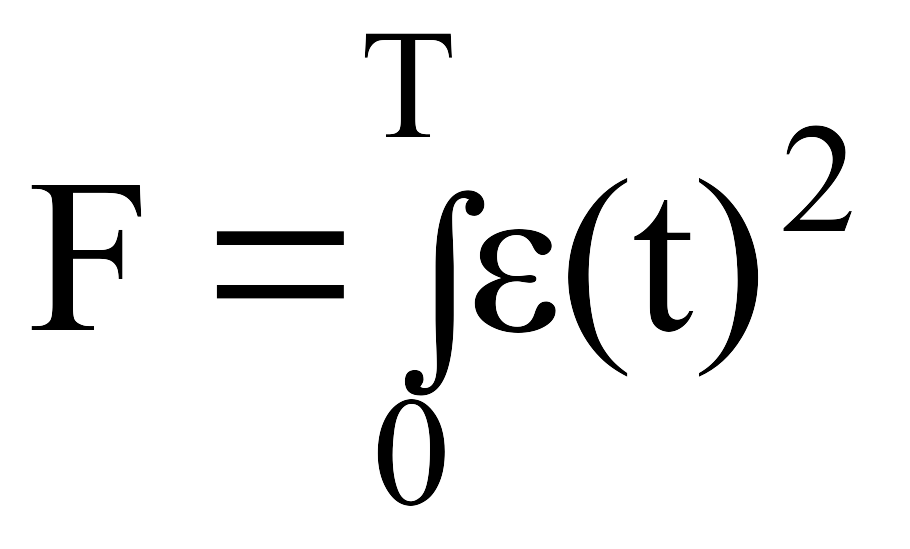
и имеет структуру для построения в пакете:

При использовании пакета Matlab для оптимизации можно воспользоваться блоком NCD Outport в среде Simulink (см. рис. 5.2). Данный блок позволяет выполнять следующие операции:

1. Задать требуемые ограничения во временной области на любой сигнал оптимизируемой системы;

2. Указать параметры, подлежащие оптимизации;

3. Указать неопределенные параметры;

4. Провести параметрическую оптимизацию системы с учетом заданных ограничений.

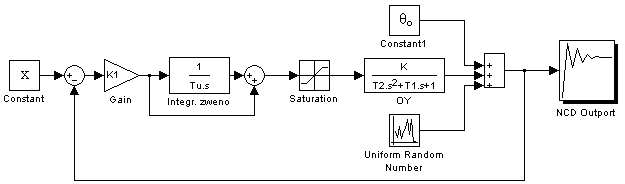
Рис. 5.2 Пример схемы оптимизации, реализованной в среде пакета Matlab

5.3 Порядок выполнения работы

5.3.1 Создать схему для оптимизации ПИ коэффициентов одним из предложенных выше способов.

Для этого в Matlab запустить Simulink, нажав в панели инструментов на пиктограмму . Создать новый документ, выполнив File/New/Model. Собрать схему, приведённую на рис. 5.2.

В блоке Saturation ввести значения в поля Upper limit (например, 100) и в Lower limit (например, 0). Допустим, что присутствует шум с равномерным законом распределения в диапазоне [-0.1; 0.1], поэтому в блоке Uniform Random Number в поле Minimum ввести -0.1, а в поле Maximum ввести 0.1.

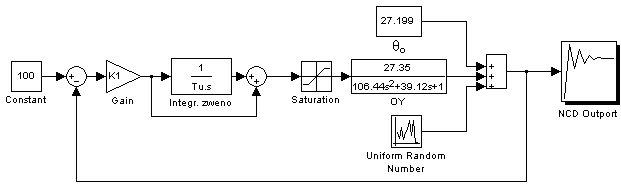
Рис. 5.3 Схема для оптимизации ПИ коэффициентов

5.3.2 Провести оптимизацию коэффициентов.

В Matlab в окне Command Window ввести значения параметров K1, Tu (см. рис. 5.4). После этого открыть блок NCD Outport, выбрать в меню Optimization/Parameteres, в появившемся окне (см. рис. 5.5) ввести оптимизируемые коэффициенты, их нижние и верхние пределы оптимизации. Запустить проект, нажав на панель инструментов на кнопку Start (см. рис. 5.6). Далее в Matlab в окне Command Window просмотреть значения параметров K1 и Tu (см. рис. 5.7).

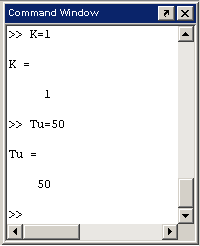
Рис. 5.4 Ввод параметров K1, Tu

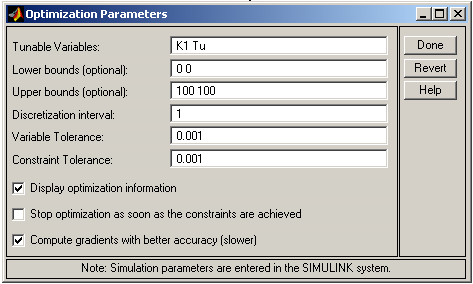
Рис. 5.5 Определение параметров оптимизации К1, Тu

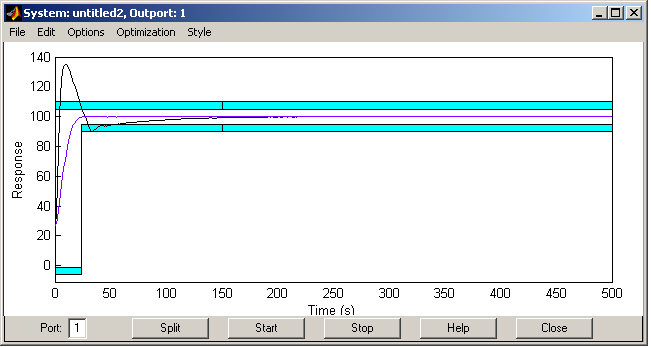
Рис. 5.6 Результат работы блока NCD Outport

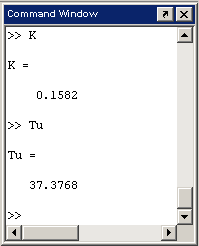
Рис. 5.7 Просмотр оптимизированных параметров К1 и Тu

5.3.3 Построить график переходного процесса выхода объекта управления при введенных оптимальных коэффициентах.

Используя Scope, просмотреть графики переходного процесса (см. рис. 5.8). Проанализировать полученные результаты (см. рис. 5.9).

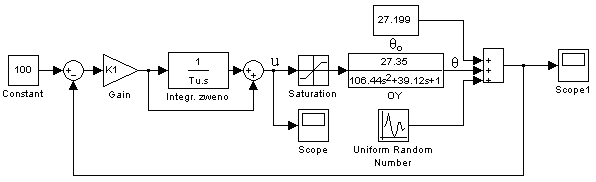
Рис. 5.8 Схема для просмотра графиков переходных процессов

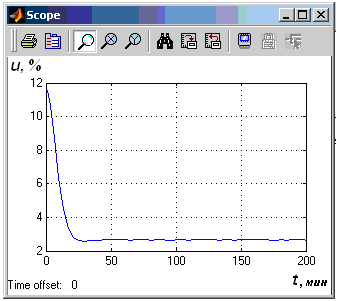
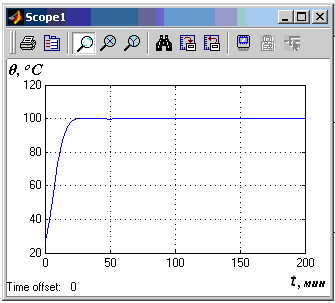
Рис. 5.9 Графики переходных процессов

5.3.4 Сделать выводы по проделанной работе.

5.4 Контрольные вопросы и задания

5.4.1 Оцените качество полученного переходного процесса.

5.4.2 Какой метод оптимизации был применен в работе?

5.4.3 Каким образом влияют настроечные коэффициенты ПИД регулятора на качество переходного процесса?

5.4.4 Для чего в схеме модели контура управления объектом (рис. 2) введен блок «saturation»?

Обязательные составляющие отчета

1. Схема оптимизации параметров ПИ регулятора.

2. Значения оптимальных параметров ПИ регулятора.

3. График переходного процесса и управляющего воздействия.

Лабораторная работа №6

Построение системы регулирования температуры

6.1 Цель работы: освоение методики построения типового контура управления с использованием контроллера.

6.2 Теоретическое введение

В АСУ ТП на нижних уровнях иерархии управления находятся подсистемы автоматического управления и регулирования технологическими агрегатами и отдельными параметрами. Функциональная структура типового контура автоматического регулирования приведена на рис. 6.1.

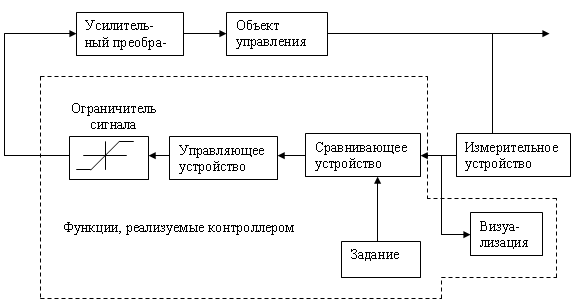
Рис. 6.1 Функциональная схема типового контура регулирования

В данной лабораторной работе рассматривается контур управления температурой в электрической нагревательной печи. Объектом управления является печь, выходная величина которой – температура – измеряется при помощи термопары или термосопротивления.

Для стабилизации значения температуры в STEP 7 при построении контура управления на базе ПИД, ПИ регуляторов рекомендуется использовать блок (TCONT_CP), который реализует функции указанных регуляторов.

Вызов блока регулятора

Схема, изображенная на рис. 6.2, показывает вызов управления в FBD. А в таблице 1 приведено описание некоторых параметров блока ПИД-регулирования (TCONT_CP).

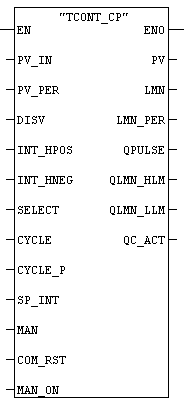
Рис. 6.2 Схема TCONT_CP

Таблица 1. Описание используемых в работе параметров блока TCONT_CP

Порядок конфигурирования блока, реализующего ПИ-закон регулирования: