1.ВЫБОР ВАРИАНТА КОНТРОЛЬНОЙ РАБОТЫ

Вариант для контрольной выбирается по номеру зачетки:

Номер зачетки (студенческого билета)	Вариант
01, 11, 21, 31, 41, 51, ...	1
02, 12, 22, 32, 42, 52, ...	2
03, 13, 23, 33, 43, 53, ...	3
04, 14, 24, 34, 44, 54, ...	4
05, 15, 25, 35, 45, 55, …	5
06, 16, 26, 36, 46, 56, …	6
07, 17, 27, 37, 47, 57, …	7
08, 18, 28, 38, 48, 58, …	8
09, 19, 29, 39, 49, 59, …	9
10, 20, 30, 40, 50, 60, …	10

Если нет студенческого билета, выбирает студент вариант по номеру в списке группы (список группы находится слева на Вашей страничке под Вашей фамилией, нажмите на название Вашей группы)

2.МеТОДИЧЕСКИЕ Указания ПО выполнению
ЗАДАНИЙ ПО ТЕМЕ
"Финансовые функции Excel"

При финансовых расчетах используются две операции: наращение и дисконтирование.

Наращение - увеличение первоначальной суммы в связи с присоединением начисленных процентов к основной сумме.

Дисконтирование - приведение стоимостной величины, относящейся к будущему, на некоторый, обычно более ранний момент времени (операция, обратная наращению).

Все финансовые функции Excel производят расчеты по схеме сложных процентов. Согласно этой схеме сумма начисленного процента присоединяется к сумме основного вклада и в следующем платежном периоде проценты начисляются на наращенную в предыдущем периоде сумму. Таким образом, база для начисления процентов каждый раз увеличивается во времени.

Важно помнить, что при использовании финансовых функций Excel учитывается направление движения денежных средств, то есть денежные суммы, участвующие в вычислениях, могут быть положительными или отрицательными. Если денежная сумма поступает, то она помечается знаком «+», если деньги отдают, то сумма помечается знаком «-».

Рассмотрим основные финансовые функции Excel, предназначенные для проведения финансово-коммерческих расчетов по кредитам и займам:

Приведем краткое описание аргументов функций:

Ставка – годовая процентная ставка;

КПер – общее количество выплат (срок, измеряемый в годах и долях года);

Плт – периодический платеж, производимый в каждый период и не меняющийся за все время займа;

Бс – будущая (наращенная) стоимость;

Пс – текущая стоимость (первоначальная сумма вложения или ссуды);

Тип – время выплаты процентов (необязательный параметр). Аргумент Тип может принимать значения:

0 – проценты начисляются в конце периода (по умолчанию);

1 – проценты начисляются в начале периода.

Традиционно проценты начисляются в конце периода и, если в условии задачи специально не оговаривается то, что время выплаты процентов – начало периода, то аргумент Тип можно не заполнять.

Расчет наращенной суммы

Пример 1: Банком выдан кредит на сумму в 1 000 000 руб. сроком на 3 года при процентной ставке - 15% годовых и начислении процентов раз в год. Рассчитать наращенную сумму.

Р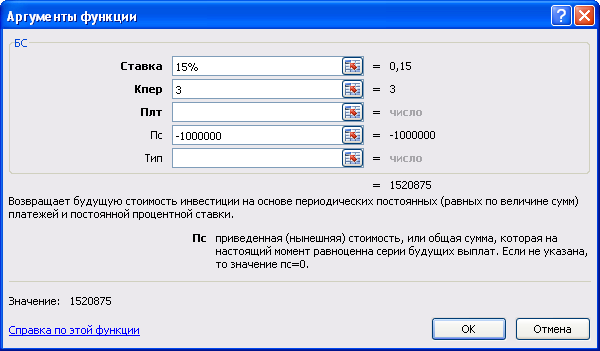
ешение: Используется функция БС

При заполнении аргументов обратите внимание на то, что аргумент Пс (первоначальная сумма кредита 1 000 000 руб.) имеет отрицательный знак, как если бы мы проводили расчеты для банка, который выплатил кредит. Ответ (будущая сумма, полученная банком по кредиту 1 520 875 руб.) будет иметь положительное значение, так как после выплаты кредита деньги в банк поступят.

Аргумент Плт не заполняем, т.к. в условиях кредита не указаны периодические (повторяющиеся из года в год) платежи.

Пример 2: Был сделан вклад 50 000 руб. на 6 месяцев под 13.5% годовых. Проценты начисляются раз в год. Рассчитать, какая сумма окажется на счете к концу срока?

Р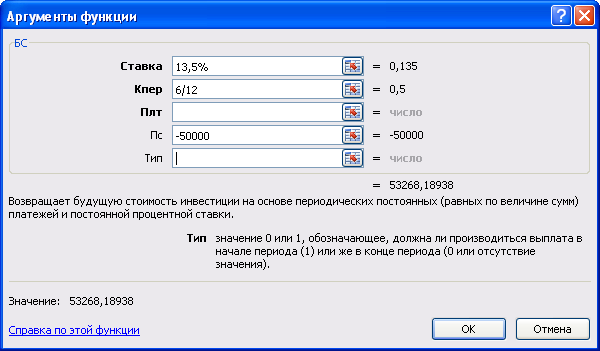
ешение: Используется функция БС

Заполняя аргументы функции, учтем, что годовая процентная ставка 13,5% действует не весь год, а только 6 месяцев, что является 6/12 частью года.

Е сли проценты начисляются несколько раз в году, аргументы финансовых функций корректируются следующим образом:

• аргумент Ставка: Годовая процентная ставка делится на количество начислений в году;

• аргумент Кпер: Количество лет умножается на количество начислений в году.

Пример3: Ссуда 5 000 000 руб., предоставлена под 9% годовых сроком на 3 года. Проценты начисляются ежеквартально. Необходимо рассчитать наращенную сумму.

Р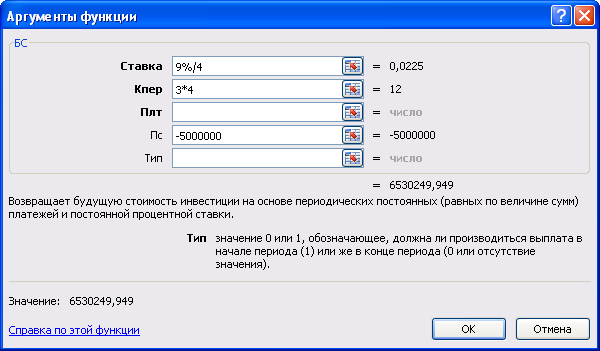
ешение: Используется функция БС

Так как начисление процентов происходит ежеквартально, то при годовой ставке 9% за один период начисления сумма вырастет на четвертую часть от заданной годовой ставки, что составит 9%/4=2,25%. Причем проценты будут начисляться каждый квартал в течении 3 лет и, таким образом, количество периодов начисления процентов будет равно 3*4=12.

Расчет дисконтированной суммы

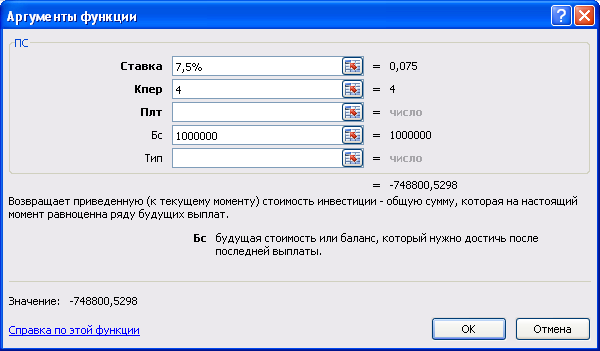
Пример: Через 4 года предприятию будет выплачена сумма 1 000 000 руб. Определить ее современную стоимость при условии, что применяется ставка сложных процентов – 7,5% годовых и проценты начисляются раз в год.

Решение: Необходим расчет первоначальной суммы вклада, следовательно, используем функцию ПС

Р
асчет срока финансовой операции

Пример: Сколько лет потребуется, чтобы погасить долг в 200 000 руб. ежегодными платежами 60 000 руб. при годовой процентной ставке 8%?

Решение: Используется функция КПЕР

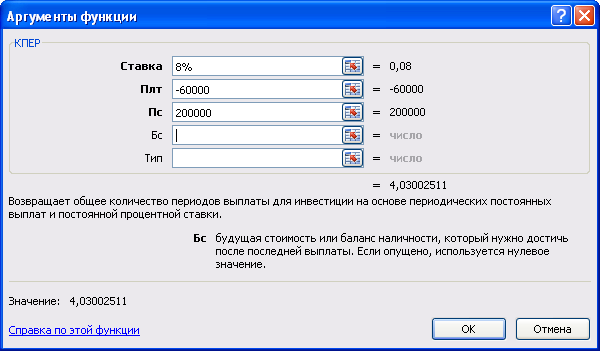
При заполнении аргументов, отметим, что первоначальная сумма 200 000 руб. была получена должником и поэтому вносится со знаком «+». Должник выплачивает 60 000 руб. в погашение суммы долга каждый год. Эта сумма является периодическим платежом (аргумент Плт) и, так как должник отдает деньги, сумма заполняется со знаком «-».

Расчет процентной ставки за период

Пример: При какой ставке сложных процентов за 7 лет сумма в 70 000 руб. увеличится в 3 раза при начислении процентов один раз в год.

Решение: Используется функция СТАВКА

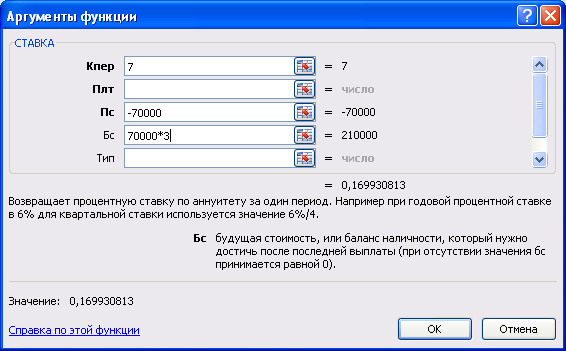
Не забудьте, что при заполнении аргументов данной функции, необходимо указать денежные суммы с разными знаками. Так, предполагаем, что первоначально вкладчик сделал вклад на 70 000 руб. (отдал деньги, следовательно, знак суммы «-»), через 7 лет он получит наращенную сумму (знак суммы «+»).

Погашение кредита с равными годовыми выплатами

П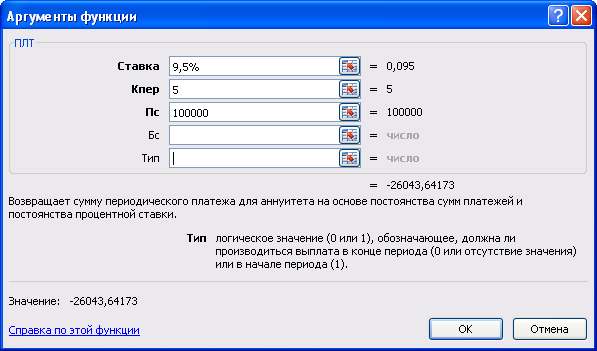
ример: Рассчитать размер ежегодного платежа для погашения кредита размером 100 000 руб., взятого в банке на 5 лет под 9,5% годовых:

Р ешение: Используется функция ПЛТ

Для получения дополнительной информации по работе с финансовыми функциями используйте справку Excel, сайт Microsoft Office (http://office.microsoft.com/ru-ru/).

3.Контрольная работа.

Вариант 1

Выполнить на компьютере с использованием финансовых функций Excel:

1. В банке был сделан вклад сроком на 1 год под 4% годовых. По окончанию срока была получена сумма в размере 35 200 рублей. Определить первоначальную сумму вклада.

2. Предприятие получило в банке кредит 6 млн. руб. под 9% годовых, сроком на 1 месяц. Определить наращенную сумму, которую предприятие должно вернуть банку.

Вариант 2

Выполнить на компьютере с использованием финансовых функций Excel:

1. В банке планируется взять кредит на сумму 100 000 руб. на 2 года. Какая ставка подходит кредитуемому, если он может выплачивать по
   5 000 руб. ежемесячно.

2. Рассчитать текущую стоимость вклада, который через три года составит 15 000 000 руб. при начислении 8,5% раз в год.

Вариант 3

Выполнить на компьютере с использованием финансовых функций Excel:

1. В течение какого срока будет погашен кредит 105 тыс. руб., выданный под 7% годовых при ежегодных выплатах 30 тыс. руб.?

2. Из какого капитала можно получить 405 тыс. руб. через 5 лет наращением по ставке 12%, если начисление процентов осуществляется раз в квартал?

Вариант 4

Выполнить на компьютере с использованием финансовых функций Excel:

1. Ссуда размером 42 тыс. руб. дана на 1 год под 7% годовых. Определить сумму, которую обязан вернуть дебитор по истечении указанного срока.

2. Иван Сергеевич Белов получил "Автокредит" в Сбербанке России на покупку нового автомобиля 600 тыс. руб. под 14,5% годовых. Условиями договора было предусмотрено, что кредит будет погашаться равными долями ежегодно в течение 3 лет. Определить ежегодные платежи Белова.

Вариант 5

Выполнить на компьютере с использованием финансовых функций Excel:

1. Предприятие получило в кредит на сумму 50 000 руб. сроком на 3 месяца под 10% годовых. Определить наращенную сумму, которую предприятие должно вернуть банку.

2. Какую сумму необходимо положить на депозит под 16,5% годовых, чтобы получить через три года 44 млн. руб. при начислении процентов раз в году?

Вариант 6

Выполнить на компьютере с использованием финансовых функций Excel:

1. Рассчитать, какая сумма окажется на счете, если 27 000 руб. положены на 4 года под 13,5% годовых. Проценты начисляются раз в полгода.

2. Рассчитайте, какую сумму надо положить на депозит, чтобы через четыре года она выросла до 20000 тыс. руб. при норме процента 9% годовых.

Вариант 7

Выполнить на компьютере с использованием финансовых функций Excel:

1. В банке был открыт депозит на срок 2 года на сумму 20 000 руб. под 5% годовых. Определить сумму, которую банк должен будет вернуть вкладчику по истечении срока депозита, при условии ежемесячного начисления процентов.

2. Сумма в 5 млн. руб. выплачивается через 5 лет. Необходимо определить ее первоначальную величину при условии, что применяется годовая ставка равная 12% .