Файл: Курсовая работа по статике расчет плоских и пространственных конструкций.docx
Добавлен: 25.10.2023
Просмотров: 134
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1 Расчет плоской шарнирной фермы
Определение реакции опор аналитическим способом.
2. Определение усилий в стержнях фермы методом вырезания узлов.
Аналитический метод определения сил реакций стержней.
Графический метод определения сил реакций в стержнях фермы.
3. РАСЧЕТ ПЛОСКИХ СОСТАВНЫХ КОНСТРУКЦИЙ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИИ
ФГБОУ ВПО ТУЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Кафедра теоретической механики
КУРСОВАЯ РАБОТА ПО СТАТИКЕ «РАСЧЕТ ПЛОСКИХ И ПРОСТРАНСТВЕННЫХ КОНСТРУКЦИЙ»
Схема 13
Выполнил: Вдовин Сергей
Руководитель: Ткач О.А.
Тула, 2022
ОГЛАВЛЕНИЕ
АННОТАЦИЯ 3
1 Расчет плоской шарнирной фермы 4
Определение реакции опор аналитическим способом. 4
2. Определение усилий в стержнях фермы методом вырезания узлов. 6
Аналитический метод определения сил реакций стержней. 6
Графический метод определения сил реакций в стержнях фермы. 10
Диаграмма Максвелла–Кремоны 12
Метод Риттера 14
3. РАСЧЕТ ПЛОСКИХ СОСТАВНЫХ КОНСТРУКЦИЙ 16
3.1. Расчет конструкции № 1 16
3.2. Расчет конструкции № 2 18
3.3. Расчет конструкции № 3 21
3.4. Расчет конструкции № 4 23
4. РАСЧЕТ ПРОСТРАНСТВЕННОЙ КОНСТРУКЦИИ 26
СПИСОК ЛИТЕРАТУРЫ 29
АННОТАЦИЯ
Исследуется равновесие твердых тел и их систем на примере таких технически важных конструкций, как плоские шарнирные фермы, балки, валы, плиты и пластинки с использованием аналитических и графических методов. Для каждой расчетной схемы составлены уравнения равновесия и определены реакции внешних и внутренних связей разными методами.
1 Расчет плоской шарнирной фермы
Схема Ф13
Дано:
Р1=10кН; Р4=15кН;a=1,2м,b=1,4м,α=900
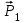
Рис.1.1
Определение реакции опор аналитическим способом.
Освободимся от связей, заменяя их действие силами реакций. Опора А – неподвижный шарнир, направление реакции в которой заранее неизвестно. Выберем систему координат и разложим её на составляющие вдоль осей координат:
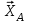 и
и 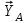 , направленные вдоль координатных осей. Стержневая опора В препятствует перемещению в направлении этого стержня, поэтому ее реакция
, направленные вдоль координатных осей. Стержневая опора В препятствует перемещению в направлении этого стержня, поэтому ее реакция
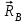 будет направлена вдоль линии стержня.
будет направлена вдоль линии стержня. Таким образом, получили свободное тело, на которое действует система активных сил
 ,
, 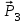 и сил реакций
и сил реакций  и
и  ,
, 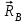 , которая находится в равновесии. Составим уравнения равновесия для заданной фермы:
, которая находится в равновесии. Составим уравнения равновесия для заданной фермы:
Рис.1.2
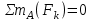 ,
, 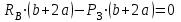 (1)
(1)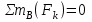 ,
, 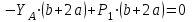 (2)
(2)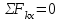 ,
, 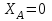 (3)
(3)Из уравнения (1) получаем:
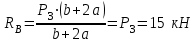
Из (2):
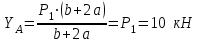
Окончательно получаем:
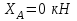 ;
; 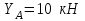 ;
; 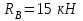
2. Определение усилий в стержнях фермы методом вырезания узлов.
Так как стержни являются невесомыми, то силы реакций будут направлены вдоль этих стержней. Стержни и узлы пронумеруем так, как показано на рис. 1.3. Определим силы реакций стержней фермы аналитически.

Рис.1.3
Аналитический метод определения сил реакций стержней.
Выбираем узел, в котором сходятся не более двух стержней силы реакции в которых неизвестны. Такими узлами в нашей задаче являются узлы I , VII. Пусть стержни условно растянуты (силы реакции направлены внутрь стержня). Если сила реакции стержня будет отрицательной, то данный стержень находится в сжатом состоянии.
Из геометрии фермы видно, что
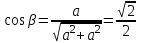
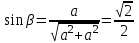 .
. 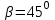
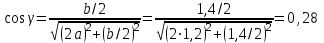
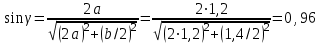 .
. 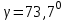 .
.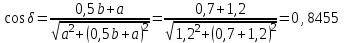
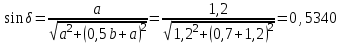 .
. 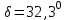 .
.
Рис.1.4
Составим уравнения равновесия для узлов I - IV:
Узел I:
 ,
, 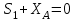
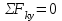 ,
, 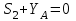
Из первого уравнения:
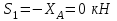 - стержень не нагружен
- стержень не нагруженИз второго уравнения:
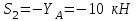 - стержень сжат
- стержень сжатУзел II:
 ,
, 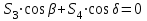
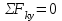 ,
, 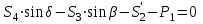
Уравнения можно записать в виде:
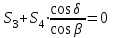
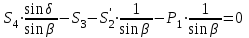
Откуда получаем, сложив уравнения:
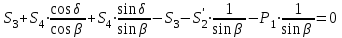
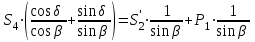
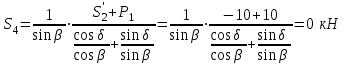 стержень не нагружен
стержень не нагруженТогда
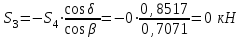 - стержень не нагружен
- стержень не нагруженУзел III:
 ,
, 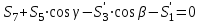
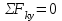 ,
, 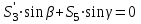
Из второго уравнения:
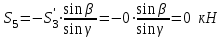 - стержень не нагружен
- стержень не нагруженИз первого уравнения:
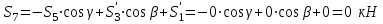 - стержень не нагружен
- стержень не нагруженУзел IV:
 ,
, 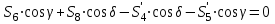
 ,
, 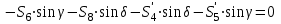
Уравнения можно записать в виде:
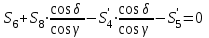
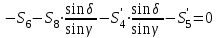
Откуда получаем, сложив уравнения:
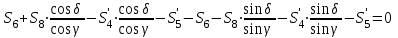
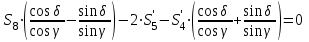
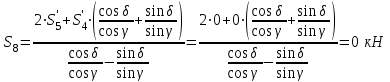 - стержень не нагружен
- стержень не нагруженТогда
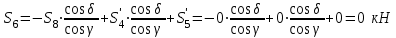 - стержень не нагружен
- стержень не нагруженРассмотрим узлы V - VII (рис.1.5)
Узел V:
 ,
, 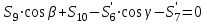
 ,
, 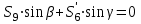
Из второго уравнения:
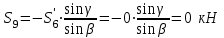 - стержень не нагружен
- стержень не нагруженИз первого уравнения:
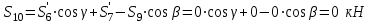 - стержень не нагружен
- стержень не нагружен
Рис.1.5
Узел VI:
 ,
, 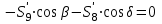
 ,
, 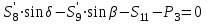
Из второго уравнения:
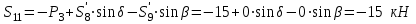 - стержень сжат.
- стержень сжат.Подставив вычисленные ранее значения в первое уравнение, проверим правильность проведенных вычислений
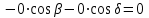
Узел VII так же используем для проверки правильности вычислений:

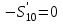

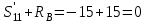
Следовательно, расчеты проведены верно.
Сведем полученные данные в таблицу:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 0 | -10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -15 |
| | сжат | | | | | | | | | сжат |
Графический метод определения сил реакций в стержнях фермы.
Силы реакций определяются из условия замкнутости силового многоугольника при равновесии для каждого из узлов фермы.
Построение силового многоугольника начнем с узла I, учитывая, что направление усилий в стержнях должно совпадать с направлением стержней фермы. Изобразим в масштабе 1 см – 2 кН силу
 . Из начала
. Из начала  проведем прямую, параллельную линии действия реакции
проведем прямую, параллельную линии действия реакции 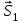 , а из конца
, а из конца  – силу
– силу 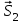 .
.Точка пересечения этих прямых будет неизвестной вершиной силового многоугольника. Определяем направления реакций стержней и измеряя длину полученных векторов с учетом масштаба находим искомые усилия. Узлы перебираем в том порядке, в котором проводили расчет реакций аналитическим методом.
Силовой многоугольник последнего узла (узла VII) строим по найденным усилиям, чтобы убедится, что он замкнут и расчеты проведены верно.