Файл: Курсовая работа по статике расчет плоских и пространственных конструкций.docx
Добавлен: 25.10.2023
Просмотров: 135
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1 Расчет плоской шарнирной фермы
Определение реакции опор аналитическим способом.
2. Определение усилий в стержнях фермы методом вырезания узлов.
Аналитический метод определения сил реакций стержней.
Графический метод определения сил реакций в стержнях фермы.
3. РАСЧЕТ ПЛОСКИХ СОСТАВНЫХ КОНСТРУКЦИЙ
Измерив полученные отрезки на плане сил с учётом выбранного масштаба, определим величины и направления неизвестных реакций, которые сведем в таблицу:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 0 | -10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -15 |
| | сжат | | | | | | | | | сжат |
Полученные результаты совпадают с результатами, полученными аналитическим методом, в пределах погрешности измерений
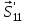
Рис.1.6
Диаграмма Максвелла–Кремоны
Строим ферму в масштабе. Изображаем все силы, действующие на ферму.
Обозначаем внешние поля — области чертежа, разделенные силами и стержнями фермы — А,В,С, D, E (рис. 1.7)
Обозначаем внутренние поля F, G, H, I,J .
Внешним нагрузкам и усилиям в стержнях даем новые имена — по соседним с силой (или стержнем) полям. Приведем таблицу соответствия имен.
| XA | Р1 | P3 | RB | YA | S1 | S2 | S3 | S4 | S5 | S6 | S7 |
| EA | AB | BC | CD | DE | DF | AF | FG | BG | GH | HI | DH |
| S8 | S9 | S10 | S11 |
| BI | IJ | DJ | CJ |
Строим многоугольник внешних сил. Выберем направление обхода фермы по часовой стрелке. Начинаем с произвольной силы, например, Р1. Откладывая в масштабе (1cм-2кН) эту силу и соблюдая
ее направление, обозначаем начальную и конечную точку строчными
буквами a и b, соответствующими направлению обхода — из поля A
в поле B. Следующая по часовой стрелке нагрузка — P3. Строим ее в точке b вслед за силой Р1. Конечную точку помечаем буквой c. Обход фермы продолжаем, пока многоугольник не замкнется. Последней будет сила реакция опоры XA, обозначенная как EA. Конец ее попадает на исходную точку.
Строим точки внутренних полей на диаграмме. Точку, соответствующую внутреннему полю, можно найти, если у этого поля построены два соседних с ним поля. Таким образом, начинать графический расчет можно с поля F, у которого соседние поля A и D определены на диаграмме. По направлению стержней AF и DF проводим линии через точки a и d диаграммы. Точка их пересечения - f. Длины afи df равны абсолютным значениям усилий в соответствующих стержнях. Аналогично рассматриваем остальные поля.
Окончательные результаты заносим в таблицу:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 0 | -10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -15 |
| | сжат | | | | | | | | | сжат |
Полученные результаты совпадают с результатами, полученными аналитическим методом, в пределах погрешности измерений и масштаба построения диаграммы

Рис.1.7
Метод Риттера
Определим усилия в стержнях 1,3,4.
Для определения нужного усилия по методу Риттера рассечем ферму по стержням 1,3,4 на части прямой I-I и рассмотрим равновесие левой части (рис.1.8). Действие отброшенной части заменим действием сил реакций.
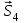
Рис.1.8
Для этого будем считать, что стержни в рассматриваемом сечении условно растянуты (силы реакций S1, S3, S4направлены внутрь стержней).
Составим уравнения равновесия для полученной части фермы:
Уравнение моментов относительно узла III:
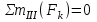 ,
, 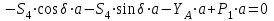
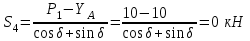
Уравнение моментов относительно узла II:
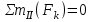 ,
, 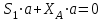

Уравнение проекций сил на ось Y:
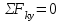 ,
, 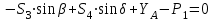
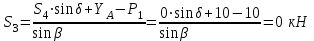
Определим усилия в стержнях 7,6,8.
Для определения нужного усилия по методу Риттера рассечем ферму по стержням 7,6,8 на части прямой II-II и рассмотрим равновесие правой части (рис.1.9). Действие отброшенной части заменим действием сил реакций.
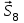
Рис.1.9
Составим уравнения равновесия для полученной части фермы:
Уравнение моментов относительно узла V:
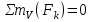 ,
, 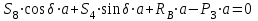
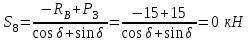
Уравнение моментов относительно узла IV:
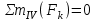 ,
, 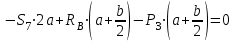
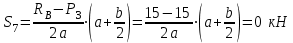
Уравнение проекций сил на ось Y:
 ,
, 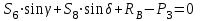
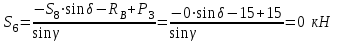
Полученные результаты совпадают с предыдущими расчетами
3. РАСЧЕТ ПЛОСКИХ СОСТАВНЫХ КОНСТРУКЦИЙ
3.1. Расчет конструкции № 1
113
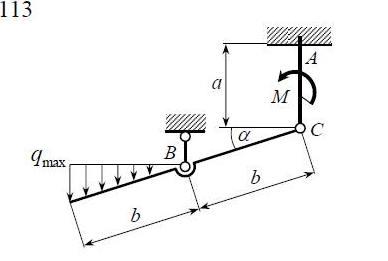 | Исходные данные: | |
| F = 10 кН; P = 17 кН; q = 6 кН/м; qmax = 10 кН/м; M = 6,2 кНм; a = 0,8 м; | b = 1,0 м; r = 0,4 м; R = 0,8 м; = 45o; = 150o. | |
| Найти: 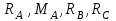 . . | ||
Решение.
1. Рассмотрим равновесие части ВС.
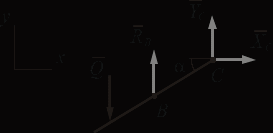
Заменяем распределенную нагрузку сосредоточенной силой
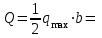 5 кН.
5 кН.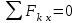
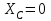 (1)
(1)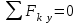
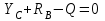 (2)
(2)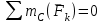
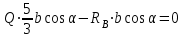 (3)
(3)2. Рассмотрим равновесие части АС.
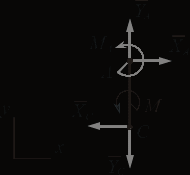
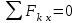
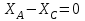 (4)
(4)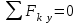
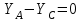 (5)
(5)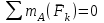
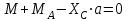 (6)
(6)Подставляя исходные данные в уравнения равновесия (1 – 6) получим:
Из (1)
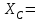 0 кН;
0 кН;(3)
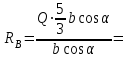 8,33 кН;
8,33 кН;(2)
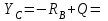 -3,33 кН;
-3,33 кН;(4)
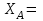 0 кН;
0 кН;(5)
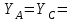 -3,33 кН;
-3,33 кН;(6)
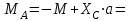 -6,2 кН.
-6,2 кН.Знак «–» при определении реакций говорит о том, что истинное направление данной реакции противоположное.
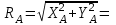 3,33 кН,
3,33 кН, 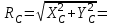 3,33 кН.
3,33 кН.Ответ:
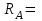 3,33 кН;
3,33 кН; 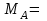 -6,2 кНм;
-6,2 кНм; 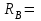 8,33 кН;
8,33 кН; 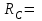 3,33 кН.
3,33 кН.3.2. Расчет конструкции № 2
213
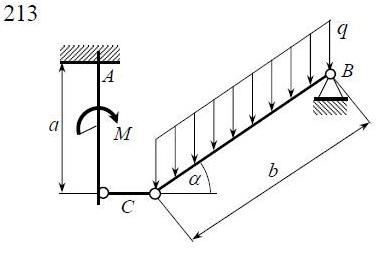 | Исходные данные: | |
| F = 10 кН; P = 17 кН; q = 6 кН/м; qmax = 10 кН/м; M = 6,2 кНм; a = 0,8 м; | b = 1,0 м; r = 0,4 м; R = 0,8 м; = 45o; = 150o. | |
| Найти:  . . | ||
Решение.
1. Рассмотрим равновесие части ВС.
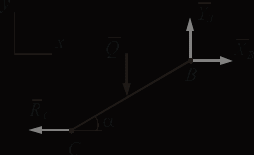
Заменяем распределенную нагрузку сосредоточенной силой
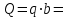 6 кН.
6 кН.
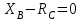 (1)
(1)
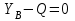 (2)
(2)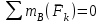
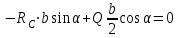 (3)
(3)2. Рассмотрим равновесие части