Добавлен: 26.10.2023
Просмотров: 113
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Если при деформации бесконечно малого отрезка (dl) приращение его деформации по оси Х равно x l δ δ , то математически расстояние между проекциями его крайних точек на этой оси определится из выражения: x l δ δ dl.
В зависимости от изменения формы тела выделяются простые виды деформации: продольного сжатия и растяжения, сдвига, объемного сжатия, а также сложные деформации изгиба и кручения, которые можно рассматривать как сочетания простых.
По симметрии относительного перемещения точек твердого тела деформации разделяются на однородные и неоднородные. При однородных деформациях параллельные линии между точками тела остаются параллельными, хотя расстояния между ними могут меняться. При этом подобные по форме фрагменты тела до и после деформации остаются подобными. При неоднородных деформациях этого не происходит. Примерами однородных деформаций являются деформации одноосного и объемного сжатия или растяжения, деформация сдвига. К неоднородным деформациям относится изгиб, кручение, обычно также пластическое течение.
Для оценки величин деформаций рассматриваются относительные деформации. Величина относительной деформации (ε) при сжатии или растяжении равна отношению изменения продольного ΔL или поперечного Δd размеров тела к первоначальной их величине (L0) или (d0), а относительная объемная деформация – это отношение изменения объема (ΔV) к его начальному значению:
ε|| = ΔL/L0 , ε┴ = Δd/d0 , εv = ΔV/V0 (4).
Можно также измерить относительную деформацию по отношению размеров тела после и до деформации. Сдвиговая деформация определяется тангенсом угла сдвига и при обычно малых их величинах – самой величиной этого угла (γ). Углы сдвига – это углы между скошенными ребрами кубика и ортогональными осями X, Y, Z , которые были параллельны ребрам до деформации(рис.2).
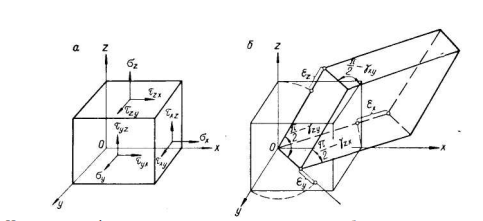
Рис.2 - Напряженно-деформированное состояние элементарного объема.
Законом Гука устанавливается линейная зависимость между напряжениями и относительными величинами упругих деформаций различных видов, коэффициентами пропорциональности между которыми являются модули упругости:
σсж = ε сж * Есж , σраст = ε р *Ер , τ = γ *G, σ = εV * Kсж, (5)
где Е сж ,
Ер - модули Юнга для деформации одноосного сжатия и растяжения;
G – модуль сдвига;
К – модуль всестороннего сжатия,
ε сж ε р εV - относительные деформации (сжатия, растяжения, объемная),
σ = 1/3(σ1 + σ2 + σ3) – напряжение всестороннего сжатия.
Из приведенных соотношений видно, что породы с относительно более высокими модулями упругости (большей жесткостью) будут испытывать меньшие деформации при одинаковых напряжениях по сравнению с менее жесткими. При одинаковых относительных деформациях уровень напряжений внутри более жесткого блока будет выше.
Модули упругости имеют размерность напряжения. Из приведенных формул следует, что упругие модули соответствуют напряжениям, при которых относительная деформация равна 1, т.е. при таком напряжении размеры блока пород должны измениться на 100%. Упругая деформация в породах и минералах не может развиваться до таких величин. Величины упругих характеристик зависят от типа пород, их состава, структуры и условий образования. В магматических породах они возрастают с увеличением их основности (Есж: от 40-60 ГПа в гранитах до 70-90 ГПа в габбро и перидотитах). Осадочные и вулканогенно-осадочные породы характеризуются минимальными в целом величинами упругих констант. Наивысшие их значения достигаются в контактово- и региональнометаморфизованных породах высоких ступеней метаморфизма.
В геологических процессах на величины упругих параметров существенное влияние оказывает ряд факторов. Это, прежде всего, скорость деформации. Поэтому различают динамические модули упругости и статические упругие параметры пород – модули деформации. Динамические параметры характеризуют абсолютно упругие деформации, происходящие в течение долей секунды. Они происходят при землетрясениях, взрывах газов в трубках взрыва, явлениям гидроразрыва вследствие превышения давления растворов в порах и трещинах над окружающим литостатическим.
При невысокой скорости деформирования связь деформаций и напряжений определяется статическими модулями деформации, которые обычно в 1.1-1.6 раза ниже динамических. Со временем происходит рост пластических деформаций, которые достигают значительных величин при напряжениях, равных пределам пластичности (текучести) пород. Это и является причиной снижения величин модулей деформации.
Существенное значение имеет тип деформации и вид напряженного состояния деформируемого блока пород. Так, обычно модуль Юнга при сжатии примерно в полтора раза больше, чем при растяжении, а при объемно-напряженном состоянии модуль упругости возрастает на 10-35%. Коэффициент Пуассона также больше при сжатии (для бетона примерно в 1.7 раза). При этом за счет волнового распространения деформаций в крупных блоках наблюдается изменение этих параметров в разных их частях. Наличие растворов в породах (особенно агрессивных) существенно снижает значения упругих констант и, в конечном счете, прочность пород.
Заключение
Распределение напряжений в горных породах сложное. Породы с разной жесткостью при деформации будут создавать разные напряжения в результате тектонического воздействия, изменения температуры, диагенеза, метаморфизма, разломов, складчатости или любых других изменений, которым подвержен горный массив. Под влиянием всего перечисленного, распределение породных напряжений становится еще более изменчивым, если геологическое строение сложное. Эти напряжения имеют значение, поскольку они влияют на поведение горных пород при добыче полезных ископаемых.
Важно знать, произойдет ли обрушение само по себе, или потребуется выполнить предварительные действия, чтобы это произошло. Если гидроразрыв рассматривается как вариант предварительной подготовки, тогда надо знать значения напряжений, поскольку гидроразрыв будет распространяться только перпендикулярно направлению минимального напряжения, если только он не будет перехвачен имеющимися в массиве трещинами/разломами.
Не менее важно знать, будут ли основные капитальные сооружения, такие как шахтные стволы, подвергаться неблагоприятному воздействию сдвижения горных пород вследствие изменения напряжений, вызванных горными работами. К сожалению, времена, когда инженеры-геологи рассматривали напряжение горных пород как некое уникальное напряжение где-то на дальних участках рудничного поля, еще не прошли. Разработчики численных моделей предпочитают использовать концепцию уникального напряжения в дальней зоне, потому что это упрощает их модели. Такой подход не годится. Даже если замеряется напряжение в дальней зоне, оно может иметь слабое отношение к напряжениям на участке, где ведутся горные работы. Их тоже необходимо измерить и иметь возможность выполнять интерполяции между измерениями. Интерполяция внутри скважины может происходить с помощью таких методов, как измерение разрушения стенки скважины или измерение овальности керна. Однако даже имея эти показатели, на каждом горном предприятии следует создать модель тех напряжений, которые имеются на этом конкретном участке горного массива. В самом простом виде для этого требуется знание гравитационную нагрузку величину тектонических деформаций.
Геологические нарушения и отработанное пространство неизменно усложняют такую модель. Однако если не делать этого, можно столкнуться с непредвиденными осложнениям в процессе дальнейшей отработки.
Список использованных источников и литературы
-
Воларович М.П., Томашевская И.С., Будников В.А. Механика горных пород при высоких давлениях. Деформационные и прочностные свойства. М.: Наука, 1979. 152 с. -
Кашников Ю.А., Ашихмин С.Г., Обшаров П.А. // Геология, геофизика и разработка нефтяных и газовых месторождений № 8, 2008. -
Мартюшев Д.А., Галкин С.В., Шелепов В.В. Влияние напряженного состояния горных пород на матричную и трещинную проницаемость в условиях различных литолого-фациальных зон турне-фаменских нефтяных залежей Верхнего Прикамья. // Вестник Московского университета. Геология. 2019. №5. С. 44-52. -
Хашпер А.Л., Аминев Т.Р., Федоров А.И., Жонин А.В. Исследование зависимости проницаемости горной породы от ее напряженнодеформированного состояния // Геол. Вестник. 2019. № 1. С. 133–140. -
Протодьяконов М. М., Ильиницкая Е. И., Карпов В. И. Методы исследования механических свойств горных пород в условиях объемного напряженного состояния // В сб. «Механические свойства горных пород». М.: Изд-во АН СССР, 1963. С. 151-156.