Файл: Пособие по подготовке к огэ приёмы и методы решения текстовых задач при подготовке к огэ по математике.docx

Задачи на смеси и сплавы

В задачах этого типа обычно присутствуют три величины, соотношение между которыми позволяет составлять уравнение:

1. 
   Концентрация (доля чистого вещества в смеси);
   
2. 
   Количество чистого вещества в смеси (или сплаве);
   
3. 
   Масса смеси (сплава).
   

Соотношение между этими величинами следующее:

Масса смеси • концентрация = количество чистого вещества
Задачи на смеси и сплавы удобно решать с помощью схем.

Схему оформляют в виде прямоугольников, разделённых на две составляющие.

Пример. Имеется два сплава меди и свинца. Один сплав содержит 15% меди, а другой 65% меди. Сколько нужно взять каждого сплава, чтобы получилось 200г сплава, содержащего 30% меди?

Решение:

Пусть первого справа было х (г), тогда второго - (200 - х) (г).

Представим условие задачи в виде схемы



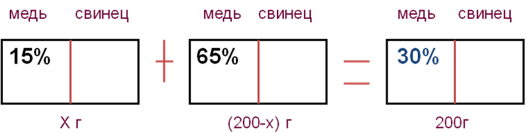
Составим уравнение по количеству меди в сплавах:

0,15х + 0,65(200 – х) = 0,3·200.

Решая это простое линейное уравнение, получаем

х = 140 (г), 200 – х = 200 – 140 = 60 (г).

Ответ: 140г, 60г.

Задания для самостоятельного решения

1. Имеются два сосуда, содержащие 40 кг и 20 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 33% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 47% кислоты. Сколько килограммов кисло-

ты содержится в первом растворе?
2. Имеются два сосуда, содержащие 24 кг и 26 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 39% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 40% кислоты. Сколько килограммов кисло-

ты содержится в первом растворе?
3. Имеются два сосуда, содержащие 48 кг и 42 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 42% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 40% кислоты. Сколько килограммов кислоты

---

содержится во втором растворе?
4. Имеются два сосуда, содержащие 22 кг и 18 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 32% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 30% кислоты. Сколько килограммов кислоты

содержится во втором растворе?

Задачи на работу

Работу характеризуют три компонента действия:

1. 
   время работы;
   
2. 
   объем работы;
   
3. 
   производительность (количество произведенной работы в единицу времени).
   

Существует следующее соотношение между этими компонентами:

Объем работы = время работы • производительность

Пример. Игорь и Паша красят забор 3 часа. Паша и Володя красят этот же забор за 4 часа, а Володя и Игорь – за 6 часов. За сколько минут мальчики покрасят забор, работая втроём.

Решение:

Пусть, работая по-отдельности, Игорь покрасит забор за x ч, Паша покрасит забор за y ч, а Володя - за z ч. Тогда

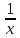- количество произведенной работы в единицу времени Игорем,

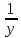- количество произведенной работы в единицу времени Пашей,

-количество произведенной работы в единицу времени Володей.

По условию задачи

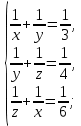
Решим систему уравнений. Для этого сложим левую и правую части системы уравнений, получим

,

= ,

= ;

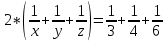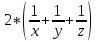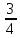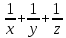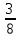Весь забор трое мальчиков покрасят за 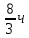, то есть за 160 минут.

Ответ: 160 мин.

Задания для самостоятельного решения

1. Первый рабочий за час делает на 10 деталей больше, чем второй, и выполняет заказ, состоящий из 60 деталей, на 3 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает первый

---

рабочий?
2. Первый рабочий за час делает на 13 детали больше, чем второй, и выполняет заказ, состоящий из 208 деталей, на 8 часов быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?
3. Три бригады изготовили вместе 266 деталей. Известно, что вторая бригада изготовила деталей в 4 раза больше, чем первая и на 5 деталей меньше, чем третья. На сколько деталей больше изготовила третья бригада, чем первая.

4. Игорь и Паша красят забор за 5 часов. Паша и Володя красят этот же забор за 6 часов, а Володя и Игорь – за 20 часов. За сколько минут мальчики покрасят забор, работая втроём?

---