Файл: Пособие по подготовке к огэ приёмы и методы решения текстовых задач при подготовке к огэ по математике.docx

Учебное пособие

по подготовке к ОГЭ

Приёмы и методы решения текстовых задач

при подготовке к ОГЭ по математике
Подготовил:

ученик 9 класса

Покутнев Никита

Руководитель:

учитель математики

Малахова Наталья Алексеевна

с. Бобровы Дворы, 2021

Содержание

Введение

Решение текстовых задач - важная тема, касающаяся математики. Еще в древности решали задачи с помощью составления уравнений.

В школьном курсе математики текстовые задачи решаются с 1 по 11 классы. Умение решать текстовые задачи с помощью уравнений важно для изучения физики и химии.

Эти задачи присутствуют в заданиях государственной итоговой аттестации для обучающихся 9 и 11 классов.

Умение решать задачи является одним из основных показателей уровня математического развития, глубины освоения учебного материала. Ученик с первых дней занятий в школе встречается с задачей. Сначала и до конца обучения в школе математическая задача неизменно помогает вырабатывать правильные математические понятия, глубже выяснять различные стороны взаимосвязей в окружающей его жизни, дает возможность применять изучаемые теоретические положения.

Текстовые задачи – традиционно трудный для значительной части школьников материал. Однако в школьном курсе математики ему придается большое значение, так как такие задачи способствуют развитию логического мышления, речи и других качеств продуктивной деятельности обучающихся.

Текстовые задачи являются важным средством обучения математике. С их помощью учащиеся получают опыт работы с величинами, постигают взаимосвязи между ними, получают опыт применения математики к решению практических (или правдоподобных) задач.

Любая текстовая задача состоит из двух частей: условия и вопроса. В условии соблюдаются сведения об объектах и некоторых величинах, характеризующих данные объекта, об известных и неизвестных значениях этих величин, об отношениях между ними.

Вопрос задачи – это указание того, что нужно найти.

Использование различных способов решения задач развивает смекалку и сообразительность, умение ставить вопросы, отвечать на них, анализировать задачные ситуации, строить план решения с учетом взаимосвязей между известными и неизвестными величинами (с учетом типа задачи), истолковывать результат каждого действия в рамках условия задачи, проверять правильность решения с помощью составления и решения обратной задачи, то есть, формировать и развивать важные общеучебные умения.

---

типы текстовых задач:

• задачи на движение;

• задачи на проценты;

• задачи на смеси и сплавы;

• задачи на работу

Процесс решения задач можно разбить на несколько этапов.

анализ условия

схематическая запись

поиск способа решения

осуществление решения

проверка решения

исследование задачи

формулировка ответа

анализ решения

Последовательное выполнение всех этапов решения задачи приводит к успешному решению.

В настоящем пособии описаны методы решения текстовых задач и представлены подробные решения различных типов таких задач. Все решения наглядно проиллюстрированы необходимыми для решения таблицами и схемами. Также по каждому типу задач предложены задания для самостоятельного решения. Тот факт, что в одном месте собраны и разборы решений, и все возможные вариации заданий для самостоятельного решения, делает пособие удобным для использования при подготовке к ОГЭ. Текстовые задачи присутствуют в ЕГЭ, поэтому пособие окажется полезным и учащимся выпускных классов.

Задачи на движение

Основными типами задач на движение являются следующие

1) задачи на движение по прямой (навстречу и вдогонку);

2) задачи на движение по замкнутой трассе;

3) задачи на движение по воде;

4) задачи на среднюю скорость;

5) задачи на движение протяжённых тел.

При решении задач на движение рассматривается зависимость между величинами: скорость, время, расстояние.

Используем памятку:

1. Путь = скорость · время

2. При движении по реке:

а) Скорость по течению = собственная скорость транспорта + скорость течения реки

б) Скорость против течения = собственная скорость транспорта - скорость течения реки

Условия задачи удобно записывать с помощью чертежа или с помощью таблицы.
Пример. Моторная лодка прошла против течения реки 60 км и вернулась в пункт отправления, затратив на обратный путь на 45 минут меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 2 км/ч. Ответ дайте в км/ч.

Решение:

Примем за x км/ч скорость лодки в неподвижной воде. Зная, что скорость течения реки равна 2 км/ч, найдем скорость лодки при движении. Ее скорость по течению реки будет составлять

---

x+2 км/ч, а против течения x-2 км/ч. И по течению, и против течения лодка прошла 60 км. Для более наглядного представления условий задачи составим таблицу, определяющую соотношения между скоростью, пройденным расстоянием и затраченным временем.

Направление движения	Скорость (V), км/ч	Время (t), ч	Пройденный путь (S), км
Против течения	x-2		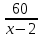60
По течению	х+2		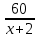60

По условию задачи, зная, что на обратный путь лодка потратила на 45 минут меньше, можем составить уравнение:



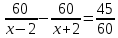
То есть



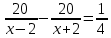
Для решения данного дробно-рационального уравнения умножим обе части равенства на произведение 4(x-2)(x+2) ≠0

В результате уравнение примет вид:

20·4(х+2)-20·4(х+2)=(х-2)(х+2),

и после элементарных преобразований (раскрытия скобок и приведения подобных слагаемых) получим неполное квадратное уравнение

х²=324,

которое имеет два различных корня х₁ = 18, корня х₂ = -18.

Так как в качестве переменной х была выбрана скорость движения лодки, то заключаем, что величина х не может быть отрицательной, так как скорость движения не может выражаться отрицательным числом. В таком случае второй корень является посторонним. Окончательно получаем: скорость лодки составляет 18 км/ч
При нахождении средней скорости движения нужно помнить, что

Средняя скорость

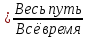
Примером задач на нахождение средней скорости движения является следующая задача из сборника типовых вариантов экзаменационных задач под редакцией И. В. Ященко.
Пример. Первую половину пути автомобиль проехал со скоростью 60 км/ч, а вторую – со скоростью 90 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

Решение:

Обозначим среднюю скорость движения v.

Пусть S (км) - длина всего пути, тогда

---

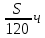
- время, затраченное на первую половину пути,

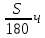- время, затраченное на вторую половину пути.

Тогда

v

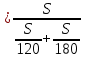
v

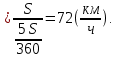
Ответ:
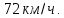
Следующая задача относится к типу задач на движение протяжённых тел.

Пример. Поезд, двигаясь равномерно со скоростью 183км/ч, проезжает мимо пешехода, идущего в том же направлении параллельно путям по платформе со скоростью 3 км/ч, за 13 секунд. Найдите длину поезда в метрах.

Решение:

Сделаем чертёж



Длина AB - это расстояние которое проходит пешеход за 13 с, двигаясь со скоростью 3 км/ч.

Длина BC – это длина поезда, обозначим её через х.

Длина AC – это расстояние которое проходит поезд за 13 с, двигаясь со скорость 183 км/ч.

AC =AB+BC

Выразим скорость пешехода и поезда в м/c.

183 км/ч ;

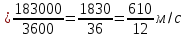3 км/ч .

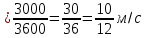Составим уравнение

,

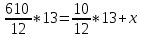решая которое получим

,

,



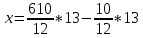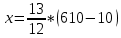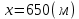
Ответ: 650 м.
Задания для самостоятельного решения

1. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 60 км. На следующий день он отправился обратно в А, увеличив скорость на 10 км/ч. По пути он сделал остановку на 3 часа, в результате чего затратил на обратный путь столько же времени, сколько на путь из А в В. найдите скорость велосипедиста на пути из А в В.
2. Из двух городов одновременно навстречу друг другу отправились два велосипедиста. проехав некоторую часть пути, первый велосипедист сделал остановку на 56 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 182 км, скорость

---

первого велосипедиста равна 13 км/ч, скорость второго – 15 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.

3. Два автомобиля одновременно отправляются в 560-километровый пробег. Первый едет со скоростью, на 10 км/ч большей, чем второй, и прибывает к финишу на 1 час раньше второго. Найдите скорость первого автомобиля.

4. Первые 105 км автомобиль ехал со скоростью 35 км/ч, следующие 120 км – со скоростью 60 км/ч, а последние 500 км – со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

5. Баржа прошла по течению реки 56 км и, повернув обратно, прошла ещё 54 км, затратив на весь путь 5 часов. Найдите собственную скорость баржи, если скорость течения реки равна 5 км/ч.

Задачи на проценты

Решение задач на проценты сводится к основным трем действиям с процентами:

1. 
   нахождение процентов от числа;
   
2. 
   нахождение числа по его процентам;
   
3. 
   нахождение процентного отношения чисел.
   

Процентом числа называется его сотая часть.

Например, 1% от числа 500 – это число 5.
Нахождение процента от числа.

Необходимо найти 3% от числа 500. Условие задачи удобно записывать в виде таблицы:

500	100%
х	3%

Составляя пропорцию 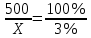и решая её, получим х=15.

Такого типа задачи можно решить и иным способом:

найти 1% от числа - для этого 500/100=5;

и полученное число умножить на количество процентов - 5·3=15.
Аналогичным образом находится число по его процентам.

Например,

60	15%
х	100%

Находим, сколько составляет 1% от числа: 60/15=4;

Затем умножаем его на 100: 4*100%=400;

Часто при решении задач проценты удобно выразить в виде десятичной дроби: 13% - 0,13 или 7,8% - 0,078.
Нахождение % отношения чисел:

Например:

Сколько % составляет 120 от 600?

Решение:
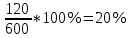
Задания для самостоятельного решения
1. Свежие фрукты содержат 78% воды, а высушенные – 22%. Сколько требуется свежих фруктов для приготовления 22 кг высушенных фруктов?
2. Свежие фрукты содержат 93% воды, а высушенные – 16%. Сколько требуется свежих фруктов для приготовления 21 кг высушенных фруктов?

---