Файл: Отчет по лабораторной работе 2 Программирование разветвляющегося вычислительного процесса.docx
Добавлен: 07.11.2023
Просмотров: 116
Скачиваний: 7
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Уфимский государственный нефтяной технический университет»
Кафедра вычислительной техники и инженерной кибернетики
Отчет
по лабораторной работе №2
«Программирование разветвляющегося вычислительного процесса»
вариант 6
Студент гр. БУС-___-01 ____________ И.И. Иванов
(подпись, дата)
Ст. преподаватель ____________ Р.М. Харисов
(подпись, дата)
Уфа 2023
Лабораторная работа N2
«Программирование разветвляющегося вычислительного процесса»
1. Постановка задачи
Разработать программу вычисления значений заданной кусочно-непрерывной функции для произвольных значений исходных данных. Подготовить исходные данные для контрольного расчета значения функции по каждой формуле. Выполнить контрольные расчеты и расчет для заданных исходных данных.
y =
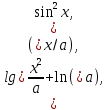
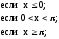
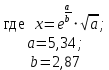
2. Анализ задачи
Задача состоит в том, чтобы по произвольно заданным значениям параметров a и b вычислить значения параметра х и функции y.
Для вычисления значения у нужно взять значения a и b, вычислить по формуле значение х. Далее проверить, соблюдается ли первое условие x≤0. Если оно соблюдается, вычислить значение у по первой формуле, записать результат, задача решена. Если же первое условие не соблюдается, нужно проверить второе условие 0
Исходных данных достаточно для решения задачи.
Проверим корректность постановки задачи, установив область определения и область возможных значений всех расчётных функций.
Область определения функции x=x(a, b) Dx={a≥0, bR, b≠0}, её возможные значения xR.
Значение y задано тремя функциями.
Область определения первой функции у=y1(x)Dу1={xR}, её возможные значения 0≤y1≤1.
Область определения второй функции у=y2(x, a)Dу2={aR, a≠0, xR, x/a>0}, её возможные значения y2R.
Область определения третьей функции у=y3(x, a)Dу3={xR, a>0}, её возможные значения у3R.
Исходные данные не противоречат области определения расчётных функций, значение у вычисляется по третьей формуле.
Подготовим тестовые примеры для проверки правильности программы (для контрольного расчёта).
а) Для проверки первой формулы выберем a=0, b=1. Тогда
x = e0/1*√0 = 0
y = sin2(0) = 0
б) Для проверки второй формулы выберем a=1, b=1. Тогда
x = e1/1*√1 = 2,718
y = lg(2,718/1) = 0,434
в) Для проверки третьей формулы выберем a=5,34, b=2,87. Тогда
x = e5,34/2,87*√5,34 = 14,854
y = 14,8542/5,34+ln(5,34) = 42,991
3. Схема алгоритма
Решение задачи описывается в виде разветвленного алгоритма (рис.1) – в виде элементарной структуры «альтернатива», вложенной в другую «альтернативу».

Work_2



2
1

Ввод
a, b



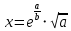
3





x≤0
да
нет
4
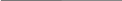






5
x≥π
6
y = sin2x


нет
да
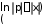
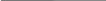







y=
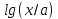
y =
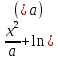
7
8


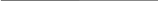


9
Вывод
y



10
конец
Рис. 1. Схема алгоритма решения задачи
4. Таблица переменных задачи
| Смысл переменных | Обозначение | Тип переменной | Примечания | |
| в алгор. | в прогр. | |||
| Исходные данные: Константа Константа Параметр | a b x | a b x | Веществ. Веществ. Веществ. | a>0 bR, b≠0 xR |
| РЕЗУЛЬТАТЫ: Функция | y | y | Веществ. | уR |
5. Текст программы на Паскале
program lab;
var a,b,x,y: real;
begin
writeln ('введите a,b');
readln(a,b);
x:=exp(a/b)*sqrt(a);
if x<=0 then y:=sin(x)*sin(x) else
if x>=Pi then y:=x*x/a+ln(a) else
y:=ln(x/a)/ln(10);
writeln('y = ',y:3:3);
end.
6. Результаты расчёта
Контрольные расчеты:
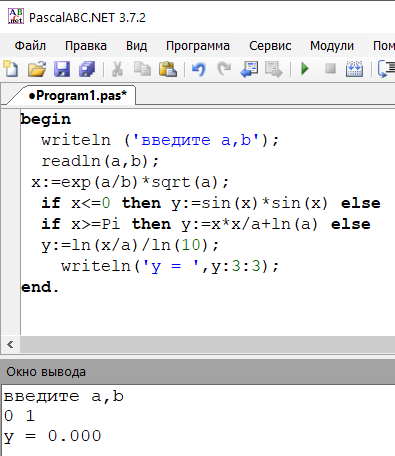
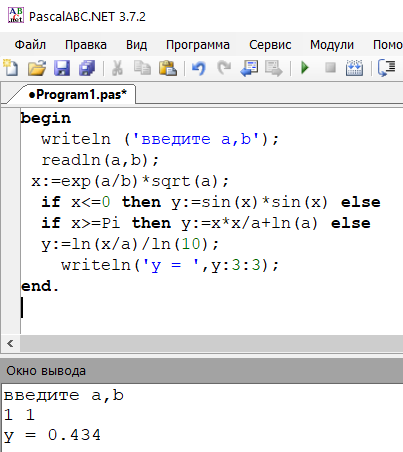
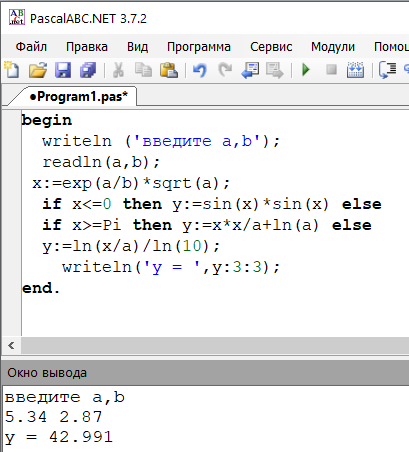
Результаты контрольных расчётов совпали с результатами ручного тестового расчёта, что подтверждает правильность программы.