Файл: Лабораторная работа по дисциплине Механика жидкости и газа (наименование дисциплины) Студент.docx

М ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное бюджетное образовательное учреждение

высшего образования
«Тольяттинский государственный университет»
Архитектурно-строительный институт

(наименование института полностью)
Промышленное и гражданское строительство

(кафедра)
ЛАБОРАТОРНАЯ РАБОТА
по дисциплине «Механика жидкости и газа»

^{(наименование дисциплины)}

Студент	Е.В. Фуфалько (И.О. Фамилия)
Группа	СТРбд-2003в
Преподаватель	С.Ш. Сайриддинов (И.О. Фамилия)

Тольятти 2023

Практическое задание для допуска к виртуальным лабораторным работам

УРАВНЕНИЕ Д.БЕРНУЛЛИ

(экспериментальное изучение и практическая реализация)

Цель работы: ознакомиться и понять смысл уравнения Бернулли, уметь применять его для решения практических задач гидродинамики.

Схема лабораторной установки

Работа производится на установке, представленной на рис.1.



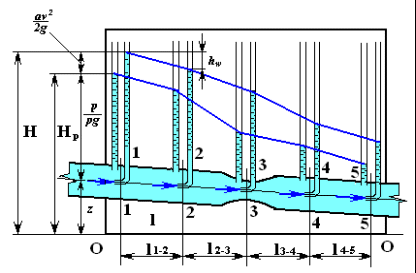
Рис. 1. Экспериментальная установка и построение линий полного и пьезометрического напоров при течении жидкости в трубе переменного сечения



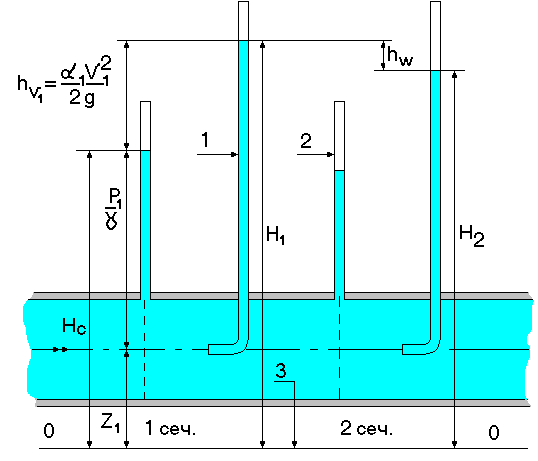
Рис.2. Пример геометрической интерпретации уравнения Бернулли

Программа работы

1. 
   Проследить за изменением величины потерь напора по длине исследуемой трубы и характером уклонов.
   
2. 
   Уяснить значение трубки Пито.
   
3. 
   Построить график изменении напоров.
   
4. 
   Ответить на контрольные вопросы.
   

---

Теоретические сведения

Закон сохранения энергии для установившегося потока несжимаемой жидкости в поле сил тяжести выражается уравнением Бернулли:

Z₁ + P₁/γ + α₁υ₁²/(2g) = Z₂ + P₂/γ + α₂υ₂²/(2g) + h_w. (1)

Уравнение (1) можно записать в виде

Z₁g + P₁g/γ + α₁υ₂²/2 = Z₂g + P₂g/γ + α₂υ₂²/2 + h_wg. (2)

Все величины, входящие в уравнения (1) и (2), имеют геометрический и энергетический смыслы (табл. 1, рис.2).

Таблица 1

Величина	Энергетический смысл	Величина	Геометрический смысл
Zg	Удельная потенциальная энергия положения	Z	Геометрическая высота от плоскости сравнения до центра тяжести сечения потока (геометрический напор)
Pg/γ	Удельная потенциальная энергия давления	P/γ	Пьезометрическая высота, замеряемая от центра тяжести сечения до уровня жидкости в пьезометре (пьезометрический напор)
αυ2/2	Удельная кинетическая энергия	αυ2/(2g)	Скоростная высота, замеряемая по разности высот в пьезометре и трубке Пито (скоростной напор)
Zg+Pg/γ+αυ2/2	Полная удельная энергия	H=Z+P/γ+ αυ2/(2g)	Гидродинамический напор (полный напор)
hwg	Потеря энергии между рассматриваемыми сечениями	hw	Потеря напора, замеряемая по разности полных напоров в двух сечениях

Каждое слагаемое уравнения Бернулли выражает энергию, отнесенную к одному килограмму веса жидкости

---

, т.е. удельную энергию, и тогда уравнение можно назвать балансом удельной энергии потока жидкости с учетом потерянной энергии.

Коэффициент α характеризует неравномерность распределения скоростей в поперечном сечении потока и представляет собой отношение истинной кинетической энергии потока к кинетической энергии, вычисленной по средней скорости. Для труб при турбулентном режиме α = 1,1. При решении инженерных практических задач коэффициент α принимают равным 1.

Уклоны. Удельная энергия вдоль потока жидкости изменяется. Если считать, что изменение ее равномерно идет вдоль потока, иногда можно потерю энергии изобразить прямыми линиями и получить геометрическую, пьезометрическую и напорную линии (1).

Геометрический уклон:

i= (Z₁ – Z₂)/l_1–2 (3)

есть тангенс угла наклона геометрической линии между сечениями к горизонтальной плоскости. Геометрический уклон показывает потерю удельной энергии положения, приходящейся на единицу длины.

Пьезометрический уклон:

J_p = ((Z₁ + P₁/γ) – (Z₂ + P₂/γ))/l_1–2. (4)

Пьезометрический уклон показывает потерю удельной потенциальной энергии, приходящейся на единицу длины.

Гидравлический уклон:

J = h_w /l_1–2 = (H₁ – H₂)/l_1–2 = ((Z₁ + P₁/γ +α₁υ₁²/(2g)) – (Z₂ + P₂/γ + α₂υ₂²/(2g)))/l_1–2.(5)

Гидравлический уклон показывает потерю полной удельной энергии, приходящейся на единицу длины.

Геометрические и пьезометрические уклоны могут быть как положительными, так и отрицательными. Гидравлический же уклон может быть только положительным, так как полная удельная энергия вдоль потока жидкости теряется при движении жидкости.

Величину средней скорости можно вычислить по уравнению:

h_υ = αυ²/(2g), откуда

υ = 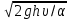. (6)

Значение α = 1,1 для турбулентного режима.

Результаты измерений и расчетов

Таблица 2

№ сеч.	l – длины меду сечениями,см	Z,геометрический напор,см	Нс статический напор, см	H – полный напор,см	hw,потерь напора, см	hv- -скоростной напор,см	V,скорость, см/с	Уклоны
								i– геометрический	Jp– пьезометрический	J– гидравлический
1	2	3	4	5	6	7	8	9	10	11
1	30,7	8,8	58	59	4	1	4,22	0,0732	0,130	0,130
2		6,55	54	55		1	4,22
	24,7				4,5			0,0737	1,335	0,182
3		4,73	21	50.5		29,5	22,94
	22,7				20,5			0,0736	-0,374	0,903
4		3,06	29.5	30		0,5	2,99
	30,8				1
								0,0734	0,032	0,032
5		0,8	28.5	29		0,5	2,99

---

Указания к заполнению таблицы

Графа 6:h_w= H₁ – H₂, разность между двумя полными напорами.

Графа 7: h_υ = H_полный – H_{статический.}

Графа8: по формуле(6).

Графа 9: по формуле (3).

Графа 10:по формуле (4).

Графа 11: по формуле (5).

Построение графика зависимости напоров от изменений длины между сечениями

После заполнения табл. 2 постройте график изменения геометрического, пьезометрического и скоростного напоров по длине трубы в соответствующем масштабе(на бумаге А4 на координатно-масштабной бумаге (на миллиметровке), как указано на образцах:рис.3(вариант1), рис.4 (вариант 2).



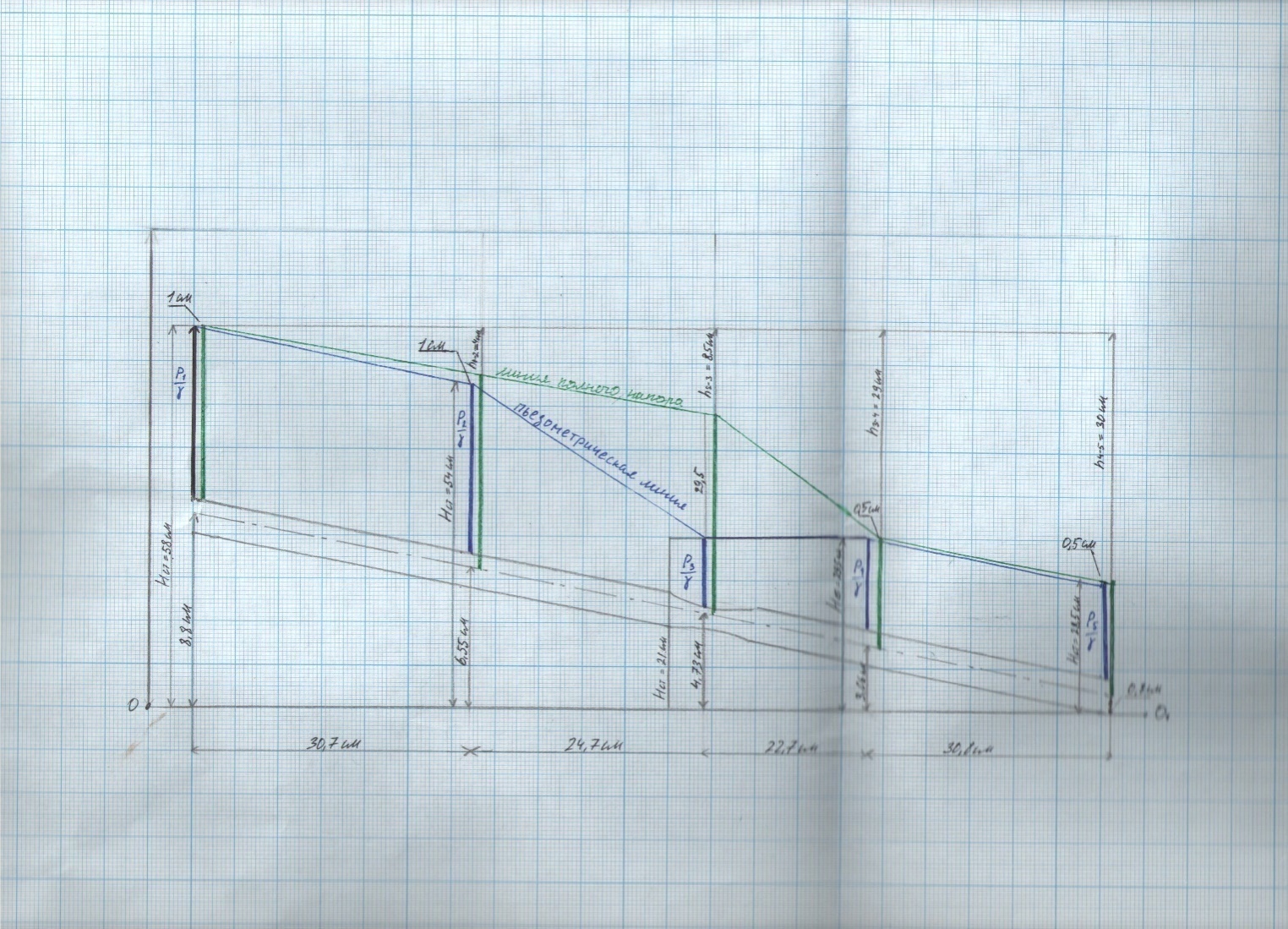
Рис. 3. Графики зависимости напоров от изменении длины трубопровода наклонного расположения (вариант 1) (на осиОYразместить напоры(Z, Н_{статический}= Z+ P/γ; H_{полный )}; наосиОХ –длины между сечениями)



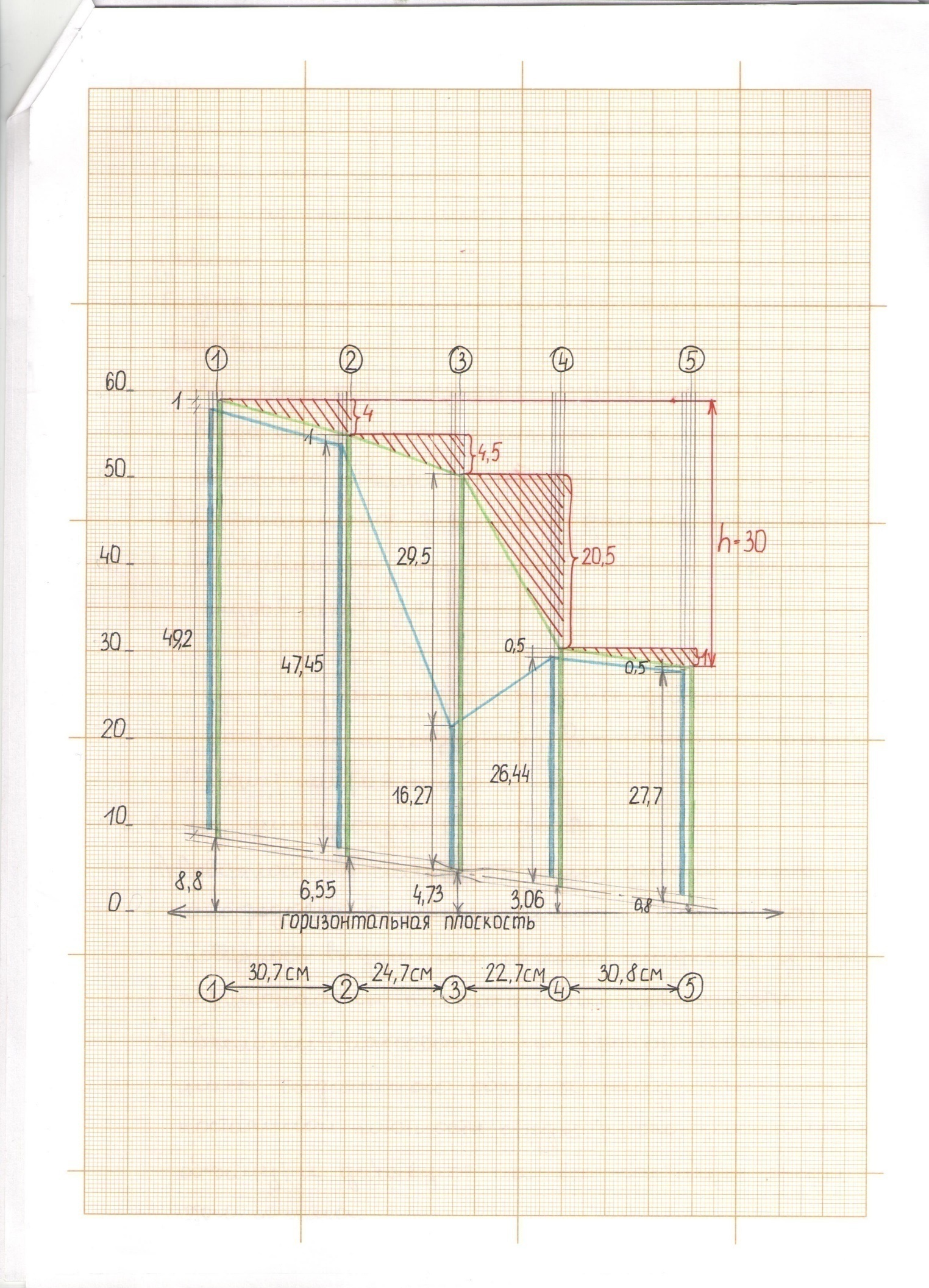
Рис. 4. Графики зависимости напоров от изменении длины трубопровода наклонного расположения (вариант 2) (на осиOYразместить напоры (Z, Н_{статический}= Z+ P/γ; H_{полный )}; на осиOX– длины между сечениями)

Общие выводы по выполненной работе:

В выполненной практической работе мы ознакомились со смыслом уравнения Бернулли, научились применять его для решения практических задач гидродинамики. С помощью уравнения Бернулли нашли потери напора между сечениями наклонного трубопровода с переменным диаметром. В характерных сечениях трубопровода найдены: скорость, скоростной напор, а также геометрический, пьезометрический и гидравлический уклоны.

---

Лабораторная работа 1

«Определение гидростатического давления жидкости»

Тема. Общие законы управления статики жидкостей: гидростатическое давление и его свойства, виды давления жидкости.
Цель работы

1. Определить цену деления стрелочного манометра в атмосферах, Н/м², Па, мм рт. ст. учитывая, что манометр имеет сто элементарных делений.

2. Определить плотность второй жидкости, считая, что в левом дифференциальном пьезометре – вода.

Схема установки представлена на рис. 1.1.



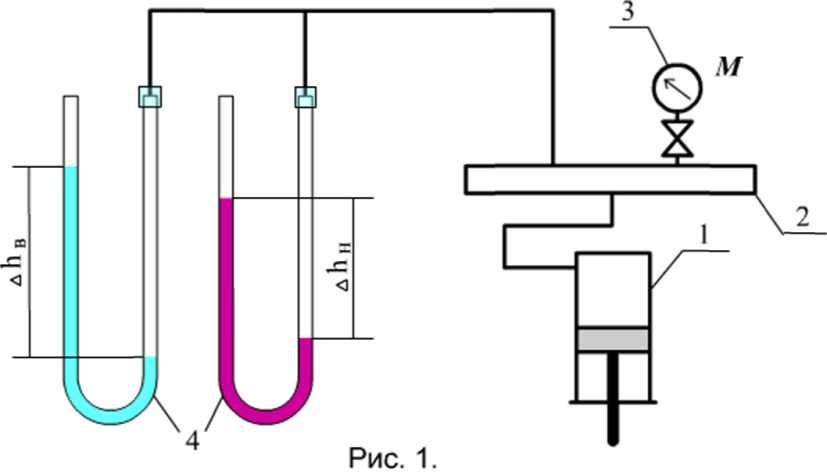
Рисунок 1.1 – Схема установки

С помощью насоса 1 в ограниченном объёме 2 создаётся соответствующее давление, которое фиксируется манометром 3, а также двумя дифференциальными пьезометрами 4, заполненными: левый – водой, правый – жидкостью неизвестной плотности.

По манометру 3 устанавливают давление, далее снимают показания дифференциальных пьезометров и, подставляя эти значения в уравнение (1.3), рассчитывают цену деления манометра 3 и плотность жидкости в правом пьезометре.

• 
  принятые формулы для расчета параметров;
  

Покажем расчет для опыта №2.

• 
  Показание водяного пьезометра Δh_В=10,8-1,6=9,2м
  
• 
  Давление в системе p = g* Δh_В= 1000*9,81*9,2=90252Па
  
• 
  Показание правого пьезометра Δh_н=6,9-4,4=2,5 м
  
• 
  Плотность жидкости в правом пьезометре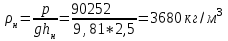
  

Цена деления манометра в [Па] Δ =90252 / 76 = 1187 (Н/м²,)/деление, Па/деление

Цена деления манометра в [атм] Δ = (90252/ (9,81·10⁴)) / 76 = 0,0121атм/деление

Цена деления манометра в [мм рт.ст.] Δ = (90252/ (9,81·10⁴ /735)) / 76 = 8,9 мм рт.ст. /деление

Таблица

результатов проведенного лабораторного эксперимента и расчетов

№ опыта	Показание водяного пьезометра, ΔhВ, м	Давление в системе, Па	Показание второго пьезометра, ΔhН, м	Плотность жидкости в правом пьезометре, ρн, кг/м3	Показание манометра рм, делений	Цена деления Δ в Н/м2, Па	Δ, атм	Δ, мм рт.ст.
1	10,2-2,4=7,8	76518	6,8-4,7=2,1	3714	67	1142	0,0116	8,6
2	10,8-1,6=9,2	90252	6,9-4,4=2,5	3680	76	1187	0,0121	8,9
3	11,4-1=10,4	102024	8,0-4,2=4	2600	86	1186	0,0121	8,9

---