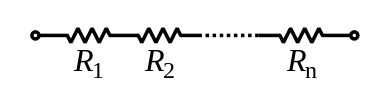Последовательное и параллельное соединение проводников

Последовательное соединение проводников.

Параллельное соединение проводников.

Последовательное и параллельное соединения  — два основных способа соединения элементов электрической цепи. При последовательном соединении все элементы связаны друг с другом так, что включающий их участок цепи не имеет ни одного узла. При параллельном соединении все входящие в цепь элементы объединены двумя узлами и не имеют связей с другими узлами, если это не противоречит условию.

При последовательном соединении проводников сила тока во всех проводниках одинакова.

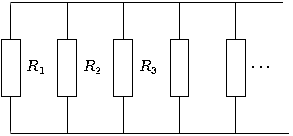
При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов. При этом величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.

Последовательное соединение

При последовательном соединении проводников сила тока в любых частях цепи одна и та же: 

Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи: 

Резисторы

Катушка индуктивности

Электрический конденсатор

.

Мемристоры

Параллельное соединение

Сила тока в неразветвленной части цепи равна сумме сил токов в отдельных параллельно соединённых проводниках: 

Напряжение на участках цепи АВ и на концах всех параллельно соединённых проводников одно и то же: 

Резистор

При параллельном соединении резисторов складываются величины, обратно пропорциональные сопротивлению (то есть общая проводимость   складывается из проводимостей каждого резистора )

Если цепь можно разбить на вложенные подблоки, последовательно или параллельно включённые между собой, то сначала считают сопротивление каждого подблока, потом заменяют каждый подблок его эквивалентным сопротивлением, таким образом находится общее (искомое) сопротивление.

Доказательство 

Для двух параллельно соединённых резисторов их общее сопротивление равно: .

Если , то общее сопротивление равно: 

При параллельном соединении резисторов их общее сопротивление будет меньше наименьшего из сопротивлений.

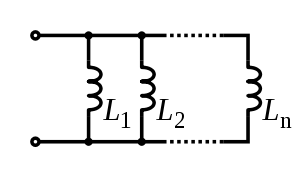
Катушка индуктивности

Электрический конденсатор

.

Мемристоры

Мощность резисторов

Как при параллельном так и при последовательном соединении резисторов, итоговая мощность будет равна сумме соединяемых резисторов. 

Преобразование звезды в треугольник и треугольника в звезду.

Соединение трех сопротивлений, имеющее вид трехлучевой звезды (рис. 2.25), называют звездой, а соединение трех сопротивлений так, что они образуют собой стороны треугольника (рис. 2.26), — треугольником. В узлах   (потенциалы их ) треугольник и звезда соединяются с остальной частью схемы (не показанной на рисунках).

Обозначим токи, подтекающие к узлам 1, 2, 3, через 

Часто при подсчете электрических цепей оказывается полезным преобразовать треугольник в звезду или, наоборот, звезду в треугольник. Практически чаще бывает необходимо преобразовывать треугольник в звезду. Если преобразование выполнить таким образом, что при одинаковых значениях потенциалов одноименных точек треугольника и звезды подтекающие к этим точкам токи одинаковы, то вся внешняя схема «не заметит» произведенной замены. Выведем формулы преобразований. С этой целью выразим токи   звезде и в треугольнике через разности потенциалов точек и соответствующие проводимости.

Для звезды

но

Рис. 2.25

Рис. 2.26

Подставим (2.24) в (2.23) и найдем 

откуда

Введем   в выражение (2.24) для тока 

Для треугольника в соответствии с обозначениями на рис. 2.26

Так как ток   в схеме рис. 2.25 равен току   в схеме рис. 2.26 при любых значениях потенциалов   то коэффициент при   в правой части (2.27) равен коэффициенту при   в правой части (2.26), а коэффициент при   в правой части (2.27) — коэффициенту при   в правой части (2.26).

Следовательно,

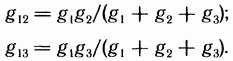
Аналогично,

Формулы (2.28) — (2.30) дают возможность определить проводимости сторон треугольника через проводимости лучей звезды.

Они имеют легко запоминающуюся структуру: индексы у проводимостей в числителе правой части соответствуют индексам у проводимости в левой части; в знаменателе — сумма проводимостей лучей звезды.

Из уравнений (2.28) — (2.30) выразим сопротивления лучей звезды   через сопротивления сторон треугольника: 

С этой целью запишем дроби, обратные (2.28) — (2.30):

где

Подставив (2.31), (2.33) и (2.34) в (2.32), получим

Следовательно,

Подставив   в (2.33), найдем

Аналогично,

Структура формул (2.35) — (2.37) аналогична структуре формул (2.28) — (2.30).

Преобразование треугольника в звезду можно пояснить, рассмотрев, например, схему рис. 2.27, а, б. На рис. 2.27, а изображена схема до преобразования, пунктиром обведен преобразуемый треугольник. На рис. 2.27, б представлена та же схема после преобразования. Расчет токов произвести для нее проще (например, методом двух узлов), чем для схемы рис. 2.27, а.

В полезности преобразования звезды в треугольник можно убедиться на примере схем рис. 2.27, в, г. На рис. 2.27, в изображена схема до преобразования, пунктиром обведена преобразуемая в треугольник звезда.

Рис. 2.27

На рис. 2.27, г представлена схема после преобразования, которая свелась к последовательному соединению сопротивлений.

Пример 24. Найти значения сопротивлений   в схеме рис. 2.27, б, если сопротивления   в схеме рис. 2.27, а равны соответственно 2,3,5 Ом.

Решение. По формуле (2.35), ; по формуле (2.36), ; по формуле (2.37), .