Индуктивный элемент позволяет учитывать явление наведения ЭДС, изменяющимся во времени магнитным потоком, и явление накопления энергии в магнитном поле реальных элементов электрической цепи. Его характеризуют зависимостью потокосцепления от тока i (вебер-амперной характеристикой) или индуктивностью . На электрических схемах индуктивный элемент изображают, как показано на рис. 3.6, а. На схеме замещения реальную индуктивную катушку можно представить в виде последовательно соединенных индуктивного и резистивного элементов.

Выделим индуктивный элемент (рис. 3.6, а). Положительные направления тока i через него, ЭДС самоиндукции   и напряжение на нем   указаны на рис. 3.6, а. Если   то . Определим разность потенциалов между точками   При перемещении от точки b к точке а идем встречно ЭДС   поэтому   и

 Дальнейшем напряжение на индуктивном элементе будем обозначать   или, просто, и без индекса

Произведение   обозначается , называется индуктивным сопротивлением и измеряется в омах (Ом):

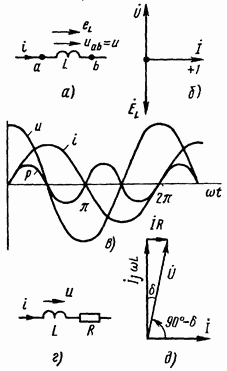
Рис. 3.6

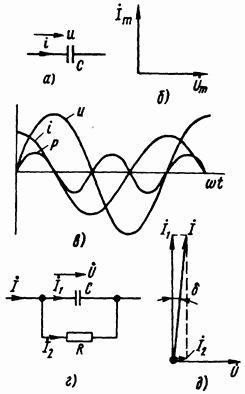
Рис. 3.7

Таким образом, индуктивный элемент (индуктивная катушка, у которой   при синусоидальном токе обладает сопротивлением, модуль которого   прямо пропорционален частоте   [см. (3.16)] — на рис. 3.6, б вектор напряжений U опережает вектор тока   на 90°. Комплекс ЭДС самоиндукции   находится в противофазе с комплексом напряжений 

Графики мгновенных значений   изображены на рис. 3.6,в.

Мгновенная мощность

проходит через нулевое значение, когда через нуль проходит либо , либо . За первую четверть периода, когда положительны,   также положительна. Площадь, ограниченная кривой   и осью абсцисс за это время, представляет собой энергию, которая взята от источника питания на создание энергий магнитного поля в индуктивной катушке. Во вторую четверть периода, когда ток в цепи уменьшается от максимума до нуля, энергия магнитного поля отдается обратно источнику питания, при этом мгновенная мощность отрицательна. За третью четверть периода у источника снова забирается энергия, за четвертую отдается и т. д. Следовательно, энергия периодически то забирается индуктивной катушкой от источника, то отдается ему обратно.

Падение напряжения на реальной индуктивной катушке равно сумме напряжений на L и на R (рис. 3.6, (9). Как видно из этого рисунка, угол между напряжением U на катушке и током   равен , причем   где   — добротность реальной индуктивной катушки. Чем больше , тем меньше .

---

Смотрите также файлы

• Изображение синусоидально изменяющихся величин на комплексной плоскости..docx

• Законы Кирхгофа..docx

• Закон Ома для участка цепи с Э.Д.С..docx

• Емкость в цепи синусоидального тока.docx

• ОПУД Тесты (250)..doc