ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 121
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ
И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
СВЯЗИ И ИНФОРМАТИКИ
Кафедра многоканальных телекоммуникационных систем
КУРСОВОЙ ПРОЕКТ
по дисциплине
Многоканальные цифровые системы передачи и средства их защиты
на тему
Реализация генерации ключей для алгоритма Эль-Гамаля в
простых и расширенных полях Галуа
Выполнил:
студент гр. БЗС1902
Смирнов Кирилл
Руководитель:
Мусатова О.Ю.
Москва 2022
Оглавление
Введение 3
Глава 1. Постановка задачи 4
Глава 2. Описание алгоритма расшифрования Эль-Гамаля в простых полях Галуа 4
2.1 Математический аппарат для простых и расширенных полей Галуа 5
2.2Расшифрование по алгоритму Эль-Гамаля 5
Глава 3. Разработка блок-схем алгоритмов программы 6
Глава 4. Код (листинг) программы 8
Глава 5. Анализ результатов 20
Выводы 20
Введение
Криптосистемы делятся на симметричные и ассиметричные. Симметричные криптосистемы – такие криптосистемы, в которых для шифрования и расшифрования применяется один и тот же ключ
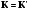 . Ассиметричные системы – такие системы, в которых шифрование и расшифрование производится при помощи разных ключей
. Ассиметричные системы – такие системы, в которых шифрование и расшифрование производится при помощи разных ключей 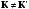 .
. Первым шагом в развитии криптографии как науки стала работа Шеннона «Теория связи в секретных системах». Эта работа позволила придать криптографии научность, а также выделить ее как отдельное направление математики. Благодаря этой работе стали развиваться симметричные криптосистемы с закрытым ключом, в которых предполагался обмен секретными ключами по закрытому каналу связи, что и является основным недостатком таких систем шифрования.
Следующий этап развития криптографии – появление ассиметричных криптосистем с открытым ключом. Этот этап начался с разработки первого алгоритма шифрования с открытым ключом, который опубликовали Диффи и Хеллман. Особенностью алгоритма было то, что можно не использовать закрытый канал связи для передачи секретных ключей, в этом случае передается лишь часть ключа по открытому каналу, а сам ключ вычисляется непосредственно абонентами.
В первую очередь применение системы, предложенной Диффи и Хеллманом, решало проблему снабжения секретными ключами всех абонентов сети: при применении старых систем каждого абонента необходимо было снабдить своим секретным ключом, что было дорого и неэффективно. При использовании алгоритма Диффи-Хеллмана ключи открыто распространяются и вычисляются математически абонентами.
После появления алгоритма Диффи-Хеллмана ассиметричные криптосистемы развивались в более сложные варианты, в том числе, в отличие от Диффи-Хеллмана, осуществляющие уже и шифрование, а не только вычисление ключей. Такими системами были, например, алгоритмы Шамира, Эль-Гамаля, RSA.
Алгоритм Эль-Гамаля позволяет осуществить шифрование информации и подписать сообщение ключами конкретного абонента, подтверждая тем самым подлинность сообщения. Таким образом, абоненты могут не только обменяться секретными сообщениями, но и убедиться в том, что получили сообщение из достоверного источника.
Основной недостаток ассиметричных систем – то, что они сложнее в реализации, чем симметричные системы, за счет того, что для вычисления ключа необходимо выполнять дополнительные операции, это снижает скорость шифрования и расшифрования.
Глава 1. Постановка задачи
При помощи программного обеспечения VisualDSP++ необходимо реализовать микропроцессорную криптографическую систему генерации ключей для алгоритма Эль-Гамаля в простых и расширенных полях Галуа
.
Для удобства решения, разобьем задачу на несколько этапов:
-
Разработка вспомогательной программы возведения в степень в простых полях Галуа. -
Разработка основной программы, реализующей генерацию ключей по алгоритму Эль-Гамаля. -
Анализ полученных результатов.
Глава 2. Описание алгоритма расшифрования Эль-Гамаля в простых полях Галуа
Алгоритм Эль-Гамаля – ассиметричная криптосистема, основанная на вычислении односторонней функции возведения в степень по модулю. Эта функция считается односторонней, так как вычисление обратного ей дискретного логарифма при больших значениях – очень трудоемкая задача.
2.1 Математический аппарат для простых и расширенных полей Галуа
Реализация криптосистем на сигнальном процессоре требует вычисления в полях Галуа, что позволяет оставаться в пределах разрядной сетки, так как при любых операциях происходит возвращение элемента в поле путем вычисления остатка, то есть деления по модулю.
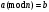 11\* MERGEFORMAT ()
11\* MERGEFORMAT ()Простые поля Галуа являются простыми числами, все операции в простых полях можно проверить обычным вычислением с помощью калькулятора. Для вычисления в простых полях можно использовать операции сложения, вычитания, умножения и деления по модулю.
-
Расшифрование по алгоритму Эль-Гамаля
Для расшифрования по алгоритму Эль-Гамаля необходимо взять два числа
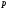 и
и 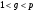 , известные всем абонентам, которые были переданы по каналу связи от абонента А, как и в случае с аутентификацией.
, известные всем абонентам, которые были переданы по каналу связи от абонента А, как и в случае с аутентификацией.Необходимо вычислить
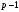 , то есть функцию Эйлера
, то есть функцию Эйлера 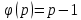 22\* MERGEFORMAT ()
22\* MERGEFORMAT () - старшая степень полинома.
- старшая степень полинома.Далее абонент Б генерирует только ему известное число
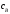 , удовлетворяющее условию
, удовлетворяющее условию 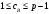 , которое является его закрытым ключом. С применением своего закрытого ключа, абонент Б вычисляет открытый ключ
, которое является его закрытым ключом. С применением своего закрытого ключа, абонент Б вычисляет открытый ключ 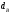 и передает его по линии связи:
и передает его по линии связи: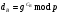 33\* MERGEFORMAT ()
33\* MERGEFORMAT ()По открытому каналу связи абонент Б получает два сообщения
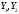 , которые являются зашифрованным сообщением абонента А. Расшифрование соответственно происходит по формуле:
, которые являются зашифрованным сообщением абонента А. Расшифрование соответственно происходит по формуле: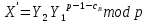 , 44\* MERGEFORMAT ()
, 44\* MERGEFORMAT ()где
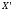 - сообщение, которое необходимо зашифровать.
- сообщение, которое необходимо зашифровать.Глава 3. Разработка блок-схем алгоритмов программы
Были разработаны блок-схемы, иллюстрирующие работу основной программы генерации ключей в простых и расширенных полях, а также их подпрограмм и основной задействованной функции – возведение в степень по модулю. Также на общей схеме указан раздел «программирование портов», соответствующий также созданию подпрограмм приема и передачи и установке флага, по которому оценивается приемник пуст и приемник полон.
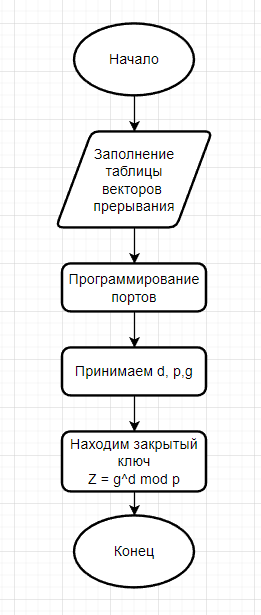
Рисунок 1. - Блок-схема общего алгоритма (одинаковый для любых полей)
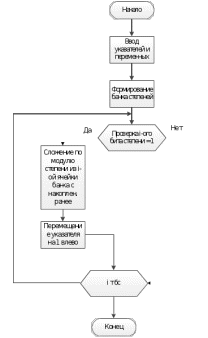
Рисунок 2. - Блок-схема возведения в степень
Глава 4. Код (листинг) программы
Программа в простых полях Галуа:
.SECTION/DM vars;
.var st=1;
// Decoding side
// Start data
.var p = 11; //First part of Open key - polinom neprivodim
.var g = 2; //Second part of Open key
.var d = 8; //Secret key
.var Z; //Third part of Open key
//Bank of stepen
.var/circ bank [16];
.SECTION/PM program;
jump start; rti; rti; rti; // RESET
rti; rti; rti; rti; // IRQ2
rti; rti; rti; rti; // IRQL1
rti; rti; rti; rti; // IRQL0
rti; rti; rti; rti; // SPORT0 Tx
rti; rti; rti; rti; // SPORT0 Rx
rti; rti; rti; rti; // IRQE
rti; rti; rti; rti; // BDMA
rti; rti; rti; rti; // SPORT1 Tx
rti; rti; rti; rti; // SPORT1 Rx
rti; rti; rti; rti; // Timer
rti; rti; rti; rti; // Power Down
// call initialization;
delen: nop;
ax0 = DM(p);
af = pass mr1;
ay0 = mr0;
ar = pass ax0;
if gt jump tttt;
llll: if lt jump rrrr;
astat = 4;
rts;
tttt: astat = 0;
divq ax0; divq ax0;divq ax0; divq ax0;
divq ax0; divq ax0;divq ax0; divq ax0;
divq ax0; divq ax0;divq ax0; divq ax0;
divq ax0; divq ax0;divq ax0; divq ax0;
divq ax0;
mr2 = 0;
my0 = ax0, ar = pass ay0;
mr = mr - ar * my0 (uu);
rts;
rrrr: sr1 = ax0;
sr = lshift sr1 by -1(hi);
astat = 0;
divq sr1; divq sr1;divq sr1; divq sr1;
divq sr1; divq sr1;divq sr1; divq sr1;
divq sr1; divq sr1;divq sr1; divq sr1;
divq sr1; divq sr1;divq sr1; divq sr1;
mr2 = 0;
my0 = ax0, ar = pass ay0;
af = tstbit 0xf of sr0;
if ne ar = ar - 1;
ay0 = ar;
mr = mr - ar * my0 (uu);
rts;
one: my0 = dm(I1,M1);
mr = mr0 * my0 (uu);
rts;
zero: my0 = dm(I1,M1);
rts;
vozv:
cntr = 15;
do nakop_bank until ce;
mr = mr0 * mr0 (uu);
call delen;
nakop_bank: dm(I0,M1) = mr0;
I1 = bank;
L1 = length(bank);
cntr = 16;
my0 = 1;
mx0 = 1;
mr = mx0 * my0 (uu);
cntr = 15;
ax0 = dm(st);
sr0 = dm(st);
do proizvedenie until ce;
af = tstbit 0 of ax0;
if ne call one;
if eq call zero;
sr = lshift sr0 by -1(lo);
proizvedenie: ax0 = sr0;
call delen;
rts;
start:
obr_sign:
ena m_mode;
I0 = bank;
L0 = length(bank);
M1 = 1;
// Finding Z = g^d mod p
mr0 = dm(g);
dm(i0,m1) = mr0;
ar = DM(d);
dm(st) = ar;
call vozv;
dm(Z) = mr0;
end: nop;
Программа в расширенных полях Галуа:
.SECTION/DM vars;
.var Yst=1;
.var uk=1;
.var st=1;
.var number;
.var poli_shifted;
.var number_shifted;
.var sum1 = 0;
.var sum2 = 1;
// Decoding side
// Start data
.var p = 67; //First part of Open key - polinom neprivodim
.var g = 17; //Second part of Open key
.var d = 13; //Secret key
.var phi=63; // phi = 2^n - 1
.var Z; //Third part of Open key
//Bank of stepen
.var/circ bank [16];
.SECTION/PM program;
jump start; rti; rti; rti; // RESET
rti; rti; rti; rti; // IRQ2
rti; rti; rti; rti; // IRQL1
rti; rti; rti; rti; // IRQL0
rti; rti; rti; rti; // SPORT0 Tx
rti; rti; rti; rti; // SPORT0 Rx
rti; rti; rti; rti; // IRQE
rti; rti; rti; rti; // BDMA
rti; rti; rti; rti; // SPORT1 Tx
rti; rti; rti; rti; // SPORT1 Rx
rti; rti; rti; rti; // Timer
rti; rti; rti; rti; // Power Down
// call initialization;
// Proverka length of number and polinom
// ar0/mr0 - number
length_prov:
dm(number) = ay1;
dm(number_shifted) = ay1;
ar = dm(p);
dm(poli_shifted) = ay1;
cycle_prov:
ay1 = dm(sum1);
ax0 = dm(poli_shifted);
ay0 = dm(poli_shifted);
none = ax0 + ay0;
if ac ar = ay1 + 1;
dm(sum1) = ar;
ay1 = dm(sum1);
ax0 = dm(number_shifted);
ay0 = dm(number_shifted);
none = ax0 + ay0;
if ac ar = ay1 + 1;
dm(sum1) = ar;
ax0 = dm(sum2);
ay0 = dm(sum1);
ar = dm(number);
ay1 = dm(number);
none = ax0 - ay0;
if lt jump del;
if eq jump viv_del;
jump cycle_prov;
pdelen:
mr0 = 0x8000;
dis ar_sat;
af = tstbit 0xf of mr1;
if ne jump obr1;
ar = mr0 and ay1;
if ne jump viv_del;
af = ay1 - mr1;
if eq jump viv0;
if lt jump length_prov;
del:
se = exp mr1 (hi);
ar = se;
ar = ar - 1;
se = ar;
sr = norm mr1 (hi);
mr1 = sr1;
af = pass ay1;
none = mr0 and af;
if ne af = mr1 xor af;
ar = abs ar;
cntr = ar;
se = -1;
sr = lshift mr0 (lo);
do tttt until ce;
mr0 = sr0;
sr = lshift mr1 (lo);
mr1 = sr0;
ar = mr0 and af;
mr1 = sr0;
if ne af = mr1 xor af;
tttt: sr = lshift mr0 (lo);
ar = pass af;
mr0 = ar;
rts;
obr1:
af = mr0 and ay1;
if eq jump viv_del;
ar = mr1 xor ay1;
rts;
viv_del:
mr0 = ar;
rts;
viv0: ay1 = 0;
mr0 = 0;
rts;
start:
obr_sign:
ena m_mode;
//Decoding side
//Finding Z = g^d mod p - Third part of Open key
mr0=dm(g);
ar=dm(d);
dm(st) = ar;
call nakop_bank;
dm(Z)=mr0;
jump end;
nakop_bank:
i0=bank;
L0=bank;
M1=1;
dm(i0,m1)=mr0;
bank_stepens:
cntr=15;
do vozvst until ce;
ar=mr0;
call umn_ab;
dm(i0,m1)=mr0;
vozvst: nop;
i0=bank;
ar=1;
dm(uk)=ar;
dm(Yst)=ar;
cntr=16;
do rez_new until ce;
mr0=dm(Yst);
sr0=dm(uk);
ay0=dm(st);
ar=sr0 and ay0;
if ne jump rez;
modify(i0,m1);
jump rez_uk;
rez:
ar=dm(i0,m1);
call umn_ab;
dm(Yst)=mr0;
rez_uk:
sr0=dm(uk);
sr=lshift sr0 by 1(lo);
dm(uk)=sr0;
rez_new: nop;
rts;
umn_ab:
dis ar_sat;
ay0 = 0;