ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 43
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Экзаменационная работа
по дисциплине: Компьютерное моделирование
Выполнил:
Группа:
Билет: 6
Проверил:
Оглавление
Задания 3
Задание 1. 4
Задание 2. 6
Задание 3 9
Список литературы 10
Задания
-
Понятие комплексной огибающей. Связь комплексной огибающей и действительного модулированного сигнала. Квадратурное смешивание.
-
Имитационное моделирование. Преимущества и недостатки. Случайные величины и их характеристики
-
Укажите первые три ненулевые аналитические частоты ДПФ, если в преобразовании участвуют 250 отсчетов, взятых с частотой дискретизации 1 кГц.
Задание 1.
Понятие комплексной огибающей. Связь комплексной огибающей и действительного модулированного сигнала. Квадратурное смешивание.
Любой реальный полосовой сигнал s(t) можно представить в комплексной форме:
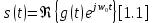
Где g(t) – комплексная огибающая, запишем ее следующим образом:
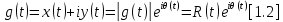
Выразим амплитуду комплексной огибающей:
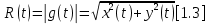
Фазу определим так:
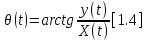
В формуле (1.1) g(t) можно назвать полосовым сообщением или данными в комплексной форме, а ejω0t – несущей в комплексной форме. Произведение этих двух величин представляет операцию модулирования, а s(t), действительная часть произведения, это переданный сигнал.
По теореме Эйлера введем комплексную запись синусоидальной несущей:
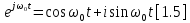
Используя формулы (1.5), (1.1) и (1.2) можно выразить следующим образом:
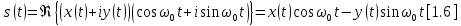
Отметим, что модулирование сигналов, выраженное в общей форме
(a + ib), умножением на (c + id), дает сигнал с переменной знака (в квадратурном члене) вида ac – bd.
Умножение сигнала на комплексную экспоненту сдвигает спектр сигнала вверх на fГц. ej2πft
Умножение сигнала на комплексную экспоненту сдвигает спектр сигнала вниз на fГц.e-j2πft
Если центральная частота полосового сигнала равна частоте комплексной экспоненты со знаком минус, то после перемножения центральная частота становится равной нулю – перенос в основную полосу.
Задание 2.
Имитационное моделирование. Преимущества и недостатки. Случайные величины и их характеристики
Имитационное моделирование – это вид моделирования, при котором логико-математическая модель исследуемого объекта (системы) представляет собой алгоритм его функционирования, реализованный в виде программного комплекса для компьютера. Т.е., программная модель, реализующая алгоритм функционирования исследуемой системы. Для настоящего времени – это не совсем точное определение: во-первых, на компьютерах сейчас практически реализуются любые виды моделей, во-вторых, наличие алгоритма не является единственной отличительной особенностью современного понимания имитационного моделирования.
Система – совокупность объектов, функционирующих и взаимодействующих друг с другом для достижения определенной цели. Для построения эффективных систем возникает необходимость их исследования с целью получения представления о внутренних отношениях между компонентами и производительности в заданных условиях эксплуатации.
Существуют следующие способы исследования систем

Система



Эксперимент с реальной системой
Эксперимент с моделью системы


Математическая модель

Физическая модель

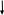


Имитационное моделирование
Аналитическое решение
Преимущества имитационного моделирования:
Большинство реальных сложных систем со стохастическим элементами не может быть точно описана аналитическими моделями, поэтому имитационное моделирование становится единственно возможным методом их исследования.
При моделировании мы можем обеспечить лучший контроль условий эксперимента, чем при экспериментировании с самой реальной системой. Моделирование позволяет оценить показатели существующей системы при фиксированных условиях эксплуатации.
Позволяет сравнивать предлагаемые альтернативные варианты проектов системы для определения лучшего.
Моделирование позволяет изучить длительный интервал функционирования систем в сжатые сроки или, наоборот, изучить более подробно работу системы в развернутый интервал времени.
Недостатки имитационного моделирования:
Каждый прогон имитационной модели позволяет получить только оценки характеристик модели для одного набора входных параметров. Всегда требуется много прогонов, что очень затратно при оптимизации. (Если возможно получение аналитической модели для оптимизации лучше использовать её.)
Разработка сложной имитационной модели требует много времени.
Если полученная модель не адекватна изучаемой системе результаты моделирования будут иметь мало полезной информации (какими бы убедительными они не казались).
Случайные величины и их характеристики
В результате эксперимента или прогона имитационной модели мы получаем случайное число, являющееся оценкой некоторого параметра системы.
Обозначим случайную величину Х, а значение которое она принимает х
Распределение случайной величины определяется интегральной функцией распределения вероятностей.
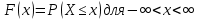
Это вероятность того, что случайная величина получит значение не превышающее х
Функция распределения непрерывной случайной величины
Функция распределения вероятностей может принимать значения от 0 до 1 и является неубывающей.
Задание 3
Укажите первые три ненулевые аналитические частоты ДПФ, если в преобразовании участвуют 250 отсчетов, взятых с частотой дискретизации 1 кГц.
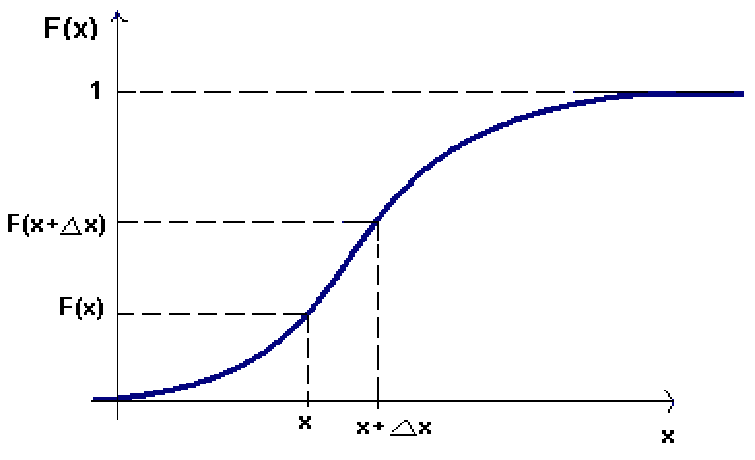
Решение:
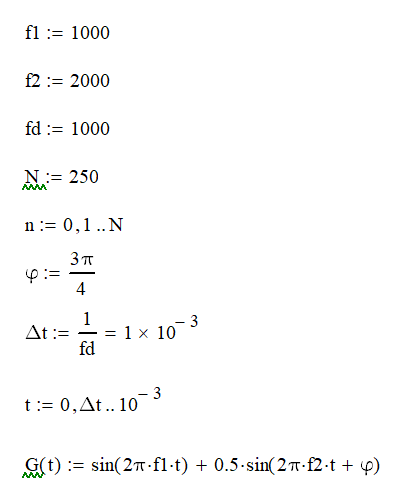
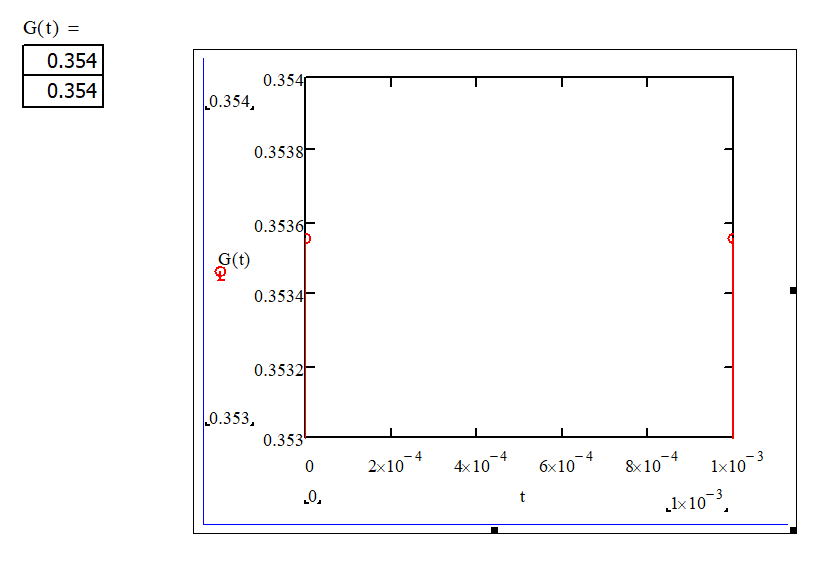
Список литературы
-
Конспект лекций. -
Ищук, А. А. Моделирование и проектирование в инфокоммуникационных технологиях [Электронный ресурс]: учебник / А. А. Ищук, И. А. Оболонин, В. И. Сединин; Сиб. гос. ун-т телекоммуникаций и информатики. - Новосибирск: СибГУТИ, 2013. - 324 с. -
Лайонс Ричард. Цифровая обработка сигналов. Пер. с англ. –М.: ООО «Бином – пресс». 2015. 656с.–ил.; -
Вершинин, А. С. Моделирование беспроводных систем связи: учебное пособие для самостоятельной работы студентов / А. С. Вершинин. — Томск: Томский государственный университет систем управления и радиоэлектроники, 2014. — 231 c.