ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 57
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство образования Республики Беларусь
Белорусский национальный технический университет
Кафедра «Гидропневмоавтоматика и гидропневмопривод»
Пояснительная записка к курсовой работе
по дисциплине «Информатика»
Тема:
Решение систем линейных уравнений. Метод Гаусса
Выполнил: Швец Александр
студент группы №10105213
Руководитель: Ермилов С.В.
Минск - 2014
РЕФЕРАТ
Пояснительная записка 28 с., 3 рис., 10 источников.
Программирование, численные математические методы, алгоритм, метод гаусса, системы уравнений, модуль CRT, идентификаторы, прямой ход, обратный ход, замена переменных
Объектом исследования является решение систем линейных уравнений методом Гаусса.
Цель работы - разработка программного продукта, позволяющего решать математические системы уравнений с помощью ЭВМ.
В процессе работы был изучен метод Гаусса, его особенности, алгоритм данного метода и возможные трудности его реализации.
Отчёт работы оформлен с использованием текстового редактора «Microsoft Word».
Применяется для решения СЛАУ в вычислительной технике.
СОДЕРЖАНИЕ
Введение
1. Цель и задачи моделирования
2. Математическое описание объекта моделирования, начальные и граничные условия
3. Алгоритм реализации задачи
4. Порядок выполнения работы
5. Использование модуля CRT
6. Таблицы индификаторов
7. Результаты расчёта и их анализ
Список использованных источников
ВВЕДЕНИЕ
В линейной алгебре рассматриваются четыре класса основных задач: решение систем линейных алгебраических уравнений (СЛАУ), вычисление определителей, нахождение обратных матриц, определение собственных значений и собственных векторов матриц. Все эти задачи имеют важное прикладное значение при решении различных проблем науки и техники. Кроме того, задачи линейной алгебры являются вспомогательными при реализации многих алгоритмов вычислительной математики, математической физики, обработки результатов экспериментальных исследований.
Для решения СЛАУ применяют в основном два класса методов: прямые и итерационные. Прямые методы дают алгоритм, по которому можно найти точное решение СЛАУ. И если бы точность была абсолютной, они бы нашли его. Реальная ЭВМ, естественно, работает с погрешностью, поэтому решение будет приближённым. Итерационные методы основаны на использовании повторяющегося процесса и позволяют получить решение в результате последовательных приближений. Прямые методы являются универсальными и применяются для решения систем сравнительно невысокого порядка (п
200). Итерационные методы выгодно использовать для СЛАУ высокого порядка со слабо заполненными матрицами.
Данная курсовая работа посвящена решению систем линейных алгебраических уравнений (СЛАУ) методом Гаусса. Этот метод решения относится к прямым методам. Системами линейных алгебраических уравнений являются системы вида:
(1)Данная нам система имеет вид:
, (2)значит, подходит под определение системы линейных алгебраических уравнений.
Данный метод является наиболее известным и популярным точным способом решения такого вида систем. Этот метод заключается в последовательном исключении неизвестных, о котором будет сказано позже.
Алгоритм метода Гаусса состоит из двух этапов: приведения матрицы к треугольному виду и нахождения неизвестных. Процесс приведения к системе с треугольной матрицей называется прямым ходом, а нахождения неизвестных - обратным. Если один из ведущих элементов равен нулю, изложенный алгоритм метода Гаусса неприменим. Тем не менее, для нормальной матрицы с ненулевым определителем всегда возможна такая перестановка уравнений, что на главной диагонали не будет нулей. В приведенном коде для простоты перестановок не делается, зато делается проверка решения, а прямой и обратный ход для наглядности вынесены в отдельные подпрограммы.
Точность результатов будет определяться точностью выполнения арифметических операций при преобразовании элементов матрицы. Для уменьшения погрешности при делении на диагональный элемент рекомендуется осуществить такую перестановку уравнений, чтобы поставить на диагональ наибольший по модулю из всех элементов рассматриваемого столбца. Такая процедура называется выбором главного элемента столбца. Контроль полученных решений можно провести путем их подстановки в исходную СЛАУ.
1. Цель и задачи моделирования
Ниже я бы хотел представить список целей и задач моделирования решения систем линейных уравнение методом Гаусса. Конечно, совершенно очевидно, что главная цель и задача данного моделирования - закрепить знания курса «Информатика», полученные за текущий курс обучения. Ведь это всё должно остаться в памяти, как не попросту потраченное время, а огромная польза, которая поможет в будущем добиваться успеха и по окончанию университета. Однако есть ещё ряд целей и задач, которые я бы предпочёл отнести к важным, и которые должны быть перечислены в данной курсовой работе.
К главным целям моделирования я бы отнёс следующие:
) научится формализации задач при моделировании;
) научится строить и использовать математические алгоритмические модели для решения математических задач;
) освоить приёмы работы с программой «Pascal»;
) закрепить и расширить знания и умения, полученные при изучении курсов «математика», «информатика».
Из задач моделирования данной программы я бы выделил:
) формирование представления о компьютерном моделировании математических задач и их решений;
) закрепление навыков и знаний, полученных при изучении курса «Информатика»;
) получение необходимого минимума знаний аналитических и численных (приближенных) методах при реализации математических моделей конкретных задач;
) ознакомление с основными принципами построения математических моделей и технологических процессов.
) научится самостоятельно составлять алгоритмы решения технических задач, составлять и реализовывать соответствующие компьютерные программы на алгоритмическом языке Паскаль.
2. Математическое описание объекта моделирования, начальные и граничные условия
Система m линейных алгебраических уравнений с n неизвестными (СЛАУ) в линейной алгебре - это система уравнений вида:
(2.1)Здесь
- количество уравнений, а 
- количество неизвестных. x1,x2, …, xn - неизвестные, которые надо определить. a11, a12, …, am n - коэффициенты системы - и b1, b2, … bm - свободные члены - предполагаются известными. Индексы коэффициентов (ai j) системы обозначают номера уравнения i и неизвестного j, при котором стоит этот коэффициент, соответственно.Система (2.1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе - неоднородной.
Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.
Решение системы (2.1) - совокупность n чисел c1, c2, …, cn, таких что подстановка каждого ci вместо xi в систему (2.1) обращает все её уравнения в тождества
Система (2.1) называется совместной
Совместная система вида (2.1) может иметь одно или более решений.
Из этого выходит главный критерий совместимости - Теорема Кронекера-Капелли:
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных и бесконечное множество решений, если ранг меньше числа неизвестных.
Доказывается она следующим образом:
Необходимость.
Пусть система совместна. Тогда существуют числа
такие, что 
. Следовательно, столбец 
является линейной комбинацией столбцов 
матрицы 
. Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что 
.Достаточность.
Пусть
. Возьмем в матрице какой-нибудь базисный минор. Так как 
, то он же и будет базисным минором и матрицы 
. Тогда, согласно теореме о базисном миноре, последний столбец матрицы будет линейной комбинацией базисных столбцов, то есть столбцов матрицы . Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы .Напомним, что рангом совместной системы называется ранг её основной матрицы (либо расширенной, так как они равны).
Плюсы метода заключаются в следующем:
) Для матриц ограниченного размера менее трудоёмкий по сравнению с другими методами.
) Позволяет однозначно установить, совместна система или нет, и если совместна, найти её решение.
) Позволяет найти максимальное число линейно независимых уравнений - ранг матрицы системы.
Решения c1, c2, …, cn и c1, c2, …, cm совместной системы вида (2.1) называются различными, если нарушается хотя бы одно из равенств:
1 = c1, c2 = c2, …, cn = cm.
Совместная система вида (2.1) называется определённой
Система линейных уравнений может быть представлена в матричной форме как:
или 
. (2.2)Здесь
- это матрица системы, 
- столбец неизвестных, а - столбец свободных членов. Если к матрице приписать справа столбец свободных членов, то получившаяся матрица называется расширенной.Основные методы решения СЛАУ следующие:
) Метод Гаусса
) Метод Крамера
) Матричный метод
В данной работе мы воспользуемся первым методом, а именно - методом Гаусса.
Метод Гаусса - классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы.
Пусть исходная система выглядит следующим образом:
(2.3)
Матрица A называется основной матрицей системы, b - столбцом свободных членов. Тогда, согласно свойству элементарных преобразований над строками, основную матрицу этой системы можно привести к ступенчатому виду (эти же преобразования нужно применять к столбцу свободных членов):
(2.4)При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных
.Тогда переменные
называются главными переменными. Все остальные называются свободными.Если хотя бы одно число
то рассматриваемая система несовместна, т.е. у неё нет ни одного решения.Пусть
. Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом (
, 
где 
- номер строки):
(2.5)
(2.4)
Если свободным переменным системы (2.3) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (2.2), то по теореме об эквивалентности при элементарных преобразованиях системы (2.2) и (2.3) эквивалентны, то есть множества их решений совпадают.
Упомянутое выше условие
для всех 
может быть сформулировано в качестве необходимого и достаточного условия совместности (по теореме Кронекера-Капелли).3. Алгоритм реализации задачи
Алгоритм реализации задачи рассмотрим на примере. Допустим, необходимо решить СЛАУ:
(3.1)где хк - неизвестные величины;
- заданные элементы расширенной матрицы системы уравнений.Из первого уравнения системы (3.1) выражаем неизвестное
(3.2)что возможно при
, в противном случае надо осуществить перестановку уравнений системы. Согласно формуле (3.2) необходимо каждый элемент первой строки расширенной матрицы СЛАУ поделить на диагональный элемент
(3.3)Затем подставляем выражение (3.2) во все остальные уравнения системы, тем самым исключаем
из всех уравнений, кроме первого. Элементы расширенной матрицы преобразуем по формуле
, где 
(3.4)В результате исключения первого неизвестного
из всех уравнений все элементы первого столбца преобразований матрицы будут равны нулю, кроме 
Неизвестное
выразим из второго уравнения системы и исключим из остальных уравнений и т.д. В результате получим СЛАУ с верхней треугольной матрицей, у которой все элементы ниже главной диагонали равны нулю.Запишем выражения для неизвестных
и преобразования эелементов расширенной матрицы системы, которые обобщают формулы (3.2)-(3.4):
,
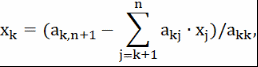
. (3.5)Второй этап решения СЛАУ называется обратным ходом метода Гаусса и состоит в последовательном определении неизвестных
по первой формуле (3.5), начиная с неизвестного 
и заканчивая .Точность результатов будет определяться точностью выполнения арифметических операций при преобразовании элементов матрицы. Для уменьшения погрешности при делении на диагональный элемент (вторая формула (3.5)) рекомендуется осуществить такую перестановку уравнений, чтобы поставить на диагональ наибольший по модулю из всех элементов рассматриваемого столбца. Такая процедура называется выбором главного элемента столбца.
Количество арифметических операций в методе Гаусса связано с размерностью системы и примерно равно 2/3
. Контроль полученных решений можно провести путем их подстановки в исходную СЛАУ и вычисления невязок 
, разностей между правыми и левыми частями уравнений:
(3.6)При малой погрешности решений величины
будут близки к нулю.
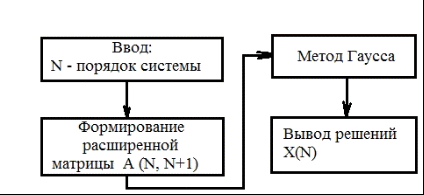
Рисунок 4.1 - Блок-схема программы решения СЛАУ методом Гаусса
Программу решения СЛАУ методом Гаусса составим из трех блоков (рисунок 1). В блоке 0 (основная программа) задаем порядок системы и обращаемся к блоку 1, в котором определяются элементы расширенной матрицы СЛАУ. Затем обращаемся к блоку 2, где реализована программа метода Гаусса. После этого выводим на дисплей результаты решения СЛАУ либо сообщение о том, что решения не существует в случае вырожденной матрицы (DET = 0).
Для общности блок 1 оформлен в виде отдельной подпрограммы. Здесь элементы расширенной матрицы задаются по строкам в диалоговом режиме с клавиатуры ПЭВМ. Хотя для других конкретных задач элементы матрицы могут определяться путем вычисления по заданному алгоритму, что потребует соответствующего изменения программы блока 1.
Блок 2 представляет собой программу метода Гаусса, которая состоит из программы прямого и обратного ходов. В процессе прямого хода осуществляется перестановка строк матрицы с целью выбора главных элементов столбцов.
Для экономии времени рекомендуется выполнение алгоритмов преобразования только с теми элементами верхней треугольной матрицы, которые будут отличными от нуля.
Особенностью программы метода Гаусса на языке Паскаль является введение новых типов переменных МАТ и VEC для матрицы А и вектора результатов X. Такое введение необходимо потому, что переменные А и X являются формальными и фактическими параметрами процедур.
Рекомендуется дополнять программы алгоритмом вычисления невязок по формуле (6), при этом следует учесть, что необходимо предусмотреть восстановление исходной расширенной матрицы системы, так как элементы матрицы изменяются в процессе приведения ее к верхнему треугольному виду. Наглядно алгоритм виден на блок-схеме, представленной ниже:
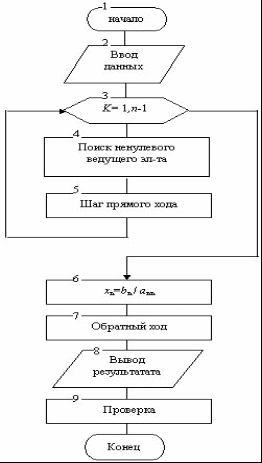
Рисунок 4.2 - Блок-схема алгоритма
программный алгебраический линейный гаусс
4. Порядок выполнения работы
Название в данной программе не самое важное, поэтому начинаем нашу программу с команды USES CRT - подключаем модуль. Далее следует раздел описаний. Описываем там используемые переменные и саму систему уравнений. Так как наша система линейных алгебраических уравнений это своеобразный массив, то и описываем её соответствующе:
var a:array[1..3,1..4] of real;:array[1..3] of real;:array[1..3] of real;,i,j,k:integer;z,r,g:real; (4.1).
Начинаем программу со слова begin. Делаем очистку экрана и присваиваем нашей переменной n значение 3. Она будет отвечать за количество уравнений системы. Далее следует writeln - указываем подсказку для пользующегося программой о том, какие данные необходимо ввести в программу. Вводим сам массив(систему) через цикл:
for i:=1 to n do
for j:=1 to n+1 do(A[i,j]); (4.2)
Делаем задержку выполнения программы командой readln и очистку экрана командой clrscr. Напоминание: после каждого оператора необходимо не забывать соответствующие знаки пунктуации. Указываем командой writeln что именно программа вывела на экран. Данная подсказка отобразится на экране вместе с полученным результатом ввода, который мы получим следующим образом:
for i:=1 to n doj:=1 to n+1 do(A[i,j]:6:2);;
end; (4.3)
Поскольку массив вводился через цикл, то и вывели мы его соответствующим образом. А поскольку цикл сложный, воспользовались операторными скобками begin и end. Понятно, что после данного оператора мы поставим точку с запятой, а не точку, т.к. это не конец программы. Снова делаем задержку выполнения программы. Далее приступаем к самому решению полученной нами матрицы. Как было описано ранее, метод Гаусса состоит из двух операций: прямой и обратный ходы. Сначала реализуем прямой ход решения системы следующим образом:
for k:=1 to n do
beginj:=k+1 to n do:=a[j,k]/a[k,k];i:=k to n do[j,i]:=a[j,i]-r*a[k,i];;[j]:=b[j]-r*b[k];
end;; (4.4)
Здесь мы осуществляем так называемый прямой ход, т.е. путём элементарных преобразований над строками приводим систему к ступенчатой или треугольной форме, либо устанавливаем, что система несовместна. А именно, среди элементов первого столбца матрицы выбираем ненулевой, перемещаем его на крайнее верхнее положение перестановкой строк и вычитаем получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним. После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркиваем и продолжаем пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходим к следующему столбцу и проделываем аналогичную операцию.
По схожему принципу производим обратный ход:
for k:=n downto 1 do:=0;j:=k+1 to n do:=a[k,j]*x[j];:=r+g;;[k]:=(b[k]-r)/a[k,k];
end; (4.5)
Таким образом мы осуществили обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения, из которого выражаем соответствующую базисную переменную (а она там всего одна) и подставляем в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки. Опять пользуемся командой writeln, чтобы уточнить что мы увидим на экране, а именно, окончательный ответ. Далее через простой цикл выводим этот ответ, а именно, корни решение данной нам системы алгебраических уравнений:
for i:=1 to n do('x[',i,']=',x[i]:0:2,' ');
writeln;; (4.6)
В этом цикле с помощью writeln и readln мы делаем задержку выполнения программы. Завершаем выполнение программы командой end. Важно: необходимо соблюдать пунктуацию программы, дабы избежать ошибки выполнения программы.
5. Использование модуля CRT
Для оформления данной программы будем использовать модуль CRT. Модуль CRT содержит набор процедур и функций управления текстовым выводом на экран дисплея, звуковым генератором и чтением символов с клавиатуры без отображения их на экране, а также переменных и констант режимов работы и цветов. Данный модуль содержит константы, переменные и подпрограммы, предназначенные для работы с консолью. В отличие от стандартного ввода-вывода, когда он осуществляется через операционную систему, подпрограммы модуля CRT работают с BIOS, и даже непосредственно с видеопамятью.
Чтобы подключить модуль используем команду «uses ctr» в строке. Эту команду следует использовать перед begin. Далее следует «begin», который сообщает о начале программы. Первое, что необходимо было сделать, это поменять фон. Моим выбором стал жёлтый цвет. Команда TextBackGround (yellow). Далее очищаем экран для применения цвета фона командой ClrScr. Изменяем цвет текста на красный командой TextColor (red). Перемещаем точку в наиболее подходящее место для последующей надписи командой GoToXY (16,5). Координаты выбираем так, что бы полная надпись легла на центр окна. Делаем надпись уже выбранным красным цветом одной из наиболее известных команд: write ('БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ'). Снова меняем положения курсора GoToXY (27,6). Координаты выбраны так, чтобы сделать надпись на строчку ниже write ('Автотракторный факультет'). Ещё раз опускаем курсор на строчку ниже командой GoToXY. Cледующая надпись: Кафедра «Гидропневмоавтоматика и гидропневмопривод». Для общей красоты оформления меняем цвет текста на голубой - TextColor(blue).
Перемещаем текст уже значительно ниже и правее - GoToXy (31,10). Следующим текстом я выбрал «Курсовая работа».
Опять меняем цвет текста командой textcolor (green). Выбранным зелёным цветом, в координатах gotoxy (34,19) пишем автора работы: «Выполнил: Швец А.Н., студент группы №10105213». Меняем положения курсора на строку ниже и указываем руководителя работы: «Руководитель работы: Eрмилов С.В.». Меняем цвет текста на розовый - textcolor (LightMagenta). Практически в самом низу (gotoxy (32,23)) дополняем оформление - write ('Минск 2014'). Делаем рациональную по времени задержку выполнения данного оформления командой delay (5500). Перемещаем курсор на строку ниже, для того чтобы текст не налаживался друг на друга. Выбираем цвет текста - blue (голубой). Это для последующей надписи от самой программы, которая просит нажать любую клавишу для продолжения.
По этому описанию составляем текст программы, который будет входить в основную программу и отвечать за её оформление. Данный текст располагаем впереди основной программы. Важно после каждого оператора не забывать знаки пунктуации, а именно «;». После слова begin ничего не ставим. В конце, после end, должна стоять точка. Текст такого моего оформления программы выглядит примерно следующим образом (пояснения работы каждой строки программы указаны после самих строк курсивом, после знака «//»:
crt; //Подключаем модуль
(yellow); //Цвет фона делаем жёлтым; //Делаем очистку экрана и применяем цвет(red); //Цвет текста делаем красным(16,5); //Перемещаем курсор в координаты (16,5)('БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ'); // Выводим на экран надпись БЕЛОРУССКИЙ
НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ(27,6); //Перемещаем курсор в координаты (27,6)('Автотракторный факультет'); //Выводим надпись Автотракторный факультет(15,7); //Перемещаем курсор в координаты (15,7)('Кафедра «Гидропневмоавтоматика и гидропневмопривод»');
//Выводим надпись Кафедра «Гидропневмоавтоматика и
гидропневмопривод»(blue); //Цвет текста делаем голубым(31,10); //Перемещаем курсор в координаты (31,10)('Курсовая работа'); //Выводим надпись Курсовая работа(8,11); //Перемещаем курсор в координаты (8,11)('Тема: Решение систем линейных алгебраических уравнений.
Метод Гаусса'); //Выводим надпись Тема: Решение систем линейных
алгебраических уравнений. Метод Гаусса.(green); //Цвет текста делаем зелёным(34,18); //Перемещаем курсор в координаты (34,18)('Выполнил: Швец А.Н., студент группы №10105213'); //Выводим
текст Выполнил: Швец А.Н., студент группы №10105213(34,19); //Перемещаем курсор в координаты (34,19)('Руководитель работы: Eрмилов С.В.'); //Выводим текст
Руководитель работы: Ермилов С.В.(LightMagenta); //Выбираем цвет текста розовым(32,23); //Перемещаем курсор в координаты (32,23)('Минск 2014'); //Выводим текст Минск 2014(5500); //Делаем задержку выполнения(18, 24); //Перемещаем курсор в координаты (18,24)(blue); //Выбираем цвет текста голубым.
6. Таблицы идентификаторов
Идентификаторы выступают в качестве имен констант, типов, переменных, процедур, модулей, программ и полей в записях. Идентификатор может иметь любую длину, однако только первые его 63 символа являются значимыми. Идентификатор должен начинаться с буквы и не может содержать пробелов. После первого символа идентификатора можно использовать буквы, цифры и символы подчеркивания. Как и в зарезервированных словах, в идентификаторах можно использовать как строчные, так и прописные буквы (компилятор их не различает).
Ниже представлены таблиц глобальных переменных программы и используемых функций и процедур.
Таблица 6.1
Глобальные переменные программы
| a,b:real; | промежуток интегрирования [a,b] где a |
| n:integer; | количество точек разбиения интервала [a,b] |
| h:real; | шаг с которым двигаются по интервалу [a,b] |
| i,j,k:integer; | вспомогательные переменные для счетчиков |
| sGaus:real; | накапливаемое значения интеграла |
| sInt:real; | реальное значение интеграла |
| kol:integer; | количество узлов для метода Гаусса 2,5 или 10 |
| nodes_file : text; | файл со справочными данными для метода Гаусса - узлы |
| NodesAndKof : array[1..10,1..2] of real; | файл со справочными данными для метода Гаусса - коэффициенты |
| GrafsFileF : text; | Формируемый файл для программы Grapher - функция |
| GrafsFileRez: text; | Формируемый файл c результатами |
| res:char; | Принимает значение y или n. Производить пересчет интеграла или нет |
Таблица 6.2
Используемые функции и процедуры
| Function f(x:real):real; | заданная функция, на интервале [a,b] |
| Function p(t,x0,x1:real):real; | преобразованная функция, на интервале [-1,1] |
| Function p(t,x0,x1:real):real; | метод Гаусса на заданном интервале [xi,xi+1] |
| Function alfa:real; | подсчет коэффициента альфа для расчета погрешности |
| Function Integral(x:real): real; | Реальное значение интеграла |
| Procedure About; | Рамочка с информацией о программе |
| Procedure EnterDate; | Ввод данных с экрана монитора |
7. Результаты расчёта и их анализ
Результатом работы является готовая программа вычисления корней СЛАУ методом Гаусса:
uses crt;a:array[1..3,1..4] of real;:array[1..3] of real;:array[1..3] of real;,i,j,k:integer;z,r,g:real;(yellow);;(red);
gotoxy (16,5);('БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ');(27,6);('Автотракторный факультет');(15,7); //('Кафедра «Гидропневмоавтоматика и гидропневмопривод»');
textcolor (blue);(31,10);('Курсовая работа');
gotoxy (8,11);('Тема: Решение систем линейных алгеброических уравнений.
Метод Гаусса');(green);(34,18);
write ('Выполнил: Швец А.Н.,студент группы №10105213');(34,19);('Руководитель работы: Eрмилов С.В.');
textcolor (LightMagenta);(32,23);('Минск 2014');(5500);(18, 24);(blue);;
n:=3;('Введите коэффициенты системы и свободные члены');
for i:=1 to n doj:=1 to n+1 do(A[i,j]);;
clrscr;('Матрица коэффициентов и свободных членов');
for i:=1 to n doj:=1 to n+1 do(A[i,j]:6:2);;;;i:=1 to n do[i]:=a[i,n+1];k:=1 to n doj:=k+1 to n do:=a[j,k]/a[k,k];i:=k to n do[j,i]:=a[j,i]-r*a[k,i];;[j]:=b[j]-r*b[k];;;k:=n downto 1 do:=0;j:=k+1 to n do:=a[k,j]*x[j];:=r+g;;[k]:=(b[k]-r)/a[k,k];;('Корни системы:');i:=1 to n do('x[',i,']=',x[i]:0:2,' ');
writeln;; end. (7.1)
Данная программа высчитывает корни системы уравнение, несколько отличающихся от точного решения. Виной этому является погрешность вычислений.
Таблица 7.1
Корни системы точные и полученные
| Корень системы | Точное решение | Полученное решение |
 | 1 | -0.16 |
 | 2 | 1.91 |
 | 3 | 3.44 |
Ниже представлю график, наглядно показывающий отличие корней:
Рисунок 7.1 - График отличия корней
Для того, чтобы уменьшить погрешность при делении на диагональный элемент, рекомендуется осуществлять такую перестановку уравнений, чтобы поставить на диагональ наибольший по модулю из всех элементов рассматриваемого столбца. Модифицированный таким образом метод Гаусса называется методом Гаусса с выбором главного элемента.
Подведём итоги:
Метод Гаусса удобно применять для систем маленькой и средней размерности (до порядка 10^4). Для больших же размерностей или разреженных матриц более эффективными представляются итерационные методы.
Рекомендуется использовать метод Гаусса с выбором главного элемента по столбцу, как более устойчивый к ошибкам, но при этом не требующий больших дополнительных затрат. В этом плане метод выбора главного элемента по строке и столбцу представляется менее эффективным, так как требует гораздо больше вычислительных затрат, но дает небольшую прибавку в точности.
Итерационное улучшение результата стоит провести 2-3 раза, если погрешность уменьшается очень медленно - возможно, матрица плохо обусловлена, тогда метод в любом случае даст не лучшие результаты - лучше попробовать применить итерационные методы.
Важно, чтобы данные считывались из файла правильно.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Методические указания по выполнению курсовой работы для студентов специальности 1-36 01 07 "Гидропневмосистемы мобильных и технологических машин". С.В. Ермило, Л.Г. Филипова, И.П. Ус. Минск, БНТУ, 2012 г.
. Жилевич, М.И. Информатика: Учебно-методическое пособие к лабораторным работам для студентов специальности 1-36 01 07 «Гидропневмосистемы мобильных и технологических машин» / М.И. Жилевич, Л.Г. Филипова. - Мн.: БНТУ, 2009. - 40 с.
. Конспект лекций по высшей математике: [в 2 ч.]. Ч.1 / Дмитрий Письменный. - 8-е изд., испр. - М.: Айрис-пресс, 2007. - 288с.: ил.
. Мудров, А.Е. Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль. - Томск: МП"РАСКО", 1991.-272 с.: ил.
. Бахвалов, Н.С. Численные методы / Н.С. Бахвалов, Н.П. Жидков, Г.М. Кобельков. - М: БИНОМ. Лаборатория знаний, 2007. - 636 с.
. Амосов А.А., Дубинский Ю.А., Копченова Н.П. Вычислительные методы для инженеров. - М.: Мир, 1998.
. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. - М.: Наука, 1970. - С. 575-576.
. Волков Е.А. Численные методы. - М.: Физматлит, 2003.
. Ильин В.А., Позняк Э.Г. Линейная алгебра: Учебник для вузов. - 6-е изд., стер. - М.: ФИЗМАТЛИТ, 2004. - 280 с.
. Офицеров, Д.В. Программирование в интегрированной среде ТурбоПаскаль. справочное пособие / Д.В. Офицеров, В.А. Старых. - Мн., «Беларусь», 1992. - 240 с.