ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 56
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Основные действия над матрицами
Сложение матриц
Суммой двух матриц A и B одних и тех же порядков m×n называется матрица C тех же порядков m×n, элементы cij которой равны
cij=aij+bij (i=1,2,...,m; j=1,2,...n).
Для обозначения суммы двух матриц используется запись:
C=A+B.
Из определения сложения матриц непосредственно следует, что эта операция обладает переместительным (коммутативным) и сочетательным (ассоциативным) свойствами:
-
A+B=B+A. -
(A+B)+C=A+(B+C).
Здесь A, B, C произвольные m×n матрицы.
Примеры сложения матриц
Рассмотрим пример сложения следующих двух матриц:
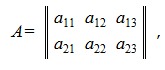
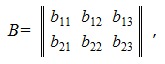
В результате сложения получим следующую матрицу:
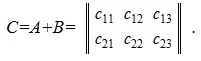
где c11=a11+b11, c12=a12+b12, c13=a13+b13, c21=a21+b21, c22=a22+b22, c23=a23+b23.
Рассмотрим следующий численный пример:
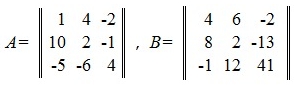
Сумма матриц A+B будет:
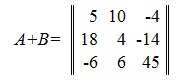
Умножение матриц
Произведением двух матриц A порядка m×n и B порядка n×k называется матрица C такая, что
| | n | | |
| cij= | ∑ | aiq ·bqj | (i=1,2,...,m; j=1,2,...k), |
| | q=1 | | |
где cij элементы матрицы C стоящие на пересечении i-ой строки и j-го столбца.
Для обозначения произведения матрицы A на матрицу B используют запись
C=A·B или C=AB.
Из сформулированного выше определения вытекает, что для умножения матрицы A на матрицу B необходимо, чтобы число столбцов матрицы A было равно числу строк матрицы B.
Операция нахождения произведения матрицы A на матрицу B называется умножением этих матриц.
Из сформулированного выше определения следует,что эта операция обладает следующими свойствами:
-
(AB)C=A(BC). -
(A+B)C=AC+BC. -
A(B+C)=AB+AC. -
(αA)B=A(αB)=α(AB)=(AB)α.
Здесь α вещественное число.
Пример умножения двух матриц
Пусть заданы матрица A размера 2×3 и матрица B размера 3×3.

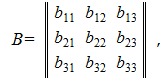
Тогда
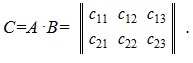
где
c11=a11b11+a12b21+a13b31, c12=a11b12+a12b22+a13b32, c13=a11b13+a12b23+a13b33, c21=a21b11+a22b21+a23b31, c22=a21b12+a22b22+a23b32, c23=a21b13+a22b23+a32b33.
Умножение матрицы в общем случае не обладает свойством коммутативности:
AB≠BA.
Пример:
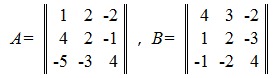
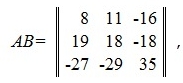 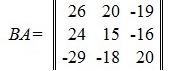 | |
Если AB=BA, то матрицы A и B называются коммутативными.
Умножение матрицы на число
Произведением матрицы A на вещественное число β называется матрица C, элементы которой равны
cij=βaij (i=1,2,...,m; j=1,2,...n).
Для обозначения произведения матрицы на число используется запись C=βA или С=Aβ. Операция составления произведения матрицы на число называется умножением матрицы на это число.
Из определения умножения матрицы на число следует, что эта операция обладает следующими свойствами:
-
(αβ)A=α(βA) -
α(A+B)=αA+αB. -
(α+β)A=αA+βB.
Примеры умножения матрицы на число
Пусть задана следующая матрица порядка 2×3:
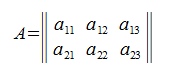
Умножим матрицу A на число f. Получим следующую матрицу:
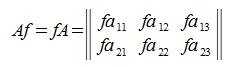
Рассмотрим численный пример.
Умножив число 4 на матрицу
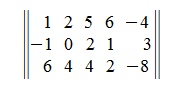
получим:
  |
Транспонированная матрица
Пусть
Для обозначения транспонированную к A матрицу используют запись AT.
Для построения транспонированной матрицы достаточно взять в качестве столбцов − соответствующие строки исходной матрицы. Например:
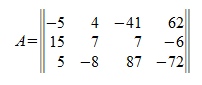
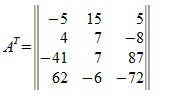
Свойства транспонированных матриц
-
(AT)T=A. -
Если матрицы A и B одинакового размера, то (A+B)T=AT+BT. -
Если определено произведение AB (т.е. количество строк A равен количеству столбцов B ), то (AB)T=BTAT. -
(βA)T=βAT, где β - некоторое число. -
Если A квадратная матрица, то определитель исходной и транспонированной матриц равны: det AT=det A. -
Разность матриц -
Разностью C двух матриц A и B одинакового размера определяется равенством -
C=A+(-1)B. -
Для обозначения разности двух матриц используется запись: -
C=A-B. -
Степень матрицы -
Пусть квадратная матрица размера n×n. Тогда степень матрицы определяется следующим образом:
квадратная матрица размера n×n. Тогда степень матрицы определяется следующим образом: -
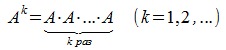
-
A0=E, -
где E-единичная матрица. -
Из сочетательного свойства умножения следует: -
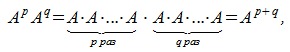
-
где p,q- произвольные целые неотрицательные числа. -
Симметричная (Симметрическая) матрица -
Матрица, удовлетворяющая условию A=AT называется симметричной матрицей. -
Для симметричных матриц имеет место равенство:
имеет место равенство: -
aij=aji ; i=1,2,...n, j=1,2,...n -