Файл: Курсовая работа по дисциплине Геодезия. Топография.docx

1.2. Задачи к разделу «Составление плана участка по материалам теодолитной и тахеометрической съёмок»

Задача № 4. Определить номенклатуру и координаты углов рамки листа топографической карты масштаба 1:10 000, в пределах которой находится пункт с заданными географическими координатами: .

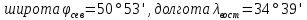В основе разграфки и номенклатуры всех топографических карт лежит разграфка и номенклатура международной карты масштаба 1:1 000 000.

Для получения листа карты масштаба 1:1 000 000 (Рисунок 6) вся земная поверхность разбивается параллелями, проведёнными через каждые 4º, на ряды и меридианами, проведёнными через 6º, на колонны.


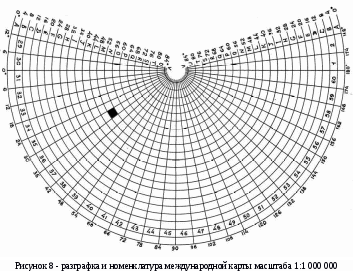
Mс-36


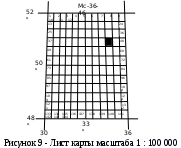
Лист карты масштаба 1:100 000 (рисунок 9) получают делением листа каты масштаба 1:1 000 000 на 144 части. Границами листов стотысячной карты будут меридианы, проведённые через 0º30’, и параллели проведённые через 0º20’. Стотысячные листы обозначаются арабскими цифрами (1,2,3 … 144).


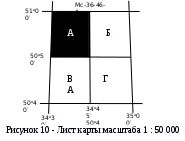
Разграфка и номенклатура листа карты масштаба 1:50 000. Лист каты масштаба 1:50 000 (Рисунок 8) получают делением листа каты масштаба 1:100 000 на 4 части Границами листов пятидесятитысячной карты будут меридианы, проведённые через 0º15’, и параллели проведённые через 0 10’. Пятидесятитысячные листы обозначаются прописными буквами русского алфавита (А, Б, В, Г).


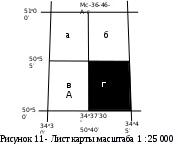
Разграфка и номенклатура листа карты масштаба 1:25 000. Лист каты масштаба 1:25 000 (рисунок 11) получают делением листа каты масштаба 1:50 000 на 4 части Границами листов двадцати пятитысячной карты будут меридианы, проведённые через 0º07’30”, и параллели проведённые через 0º05’.Двадцати пятитысячные листы обозначаются строчными буквами русского алфавита (а, б, в, г).

---

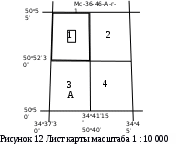
Разграфка и номенклатура листа карты масштаба 1:10 000. Лист каты масштаба 1:10 000 (Рисунок 12) получают делением листа каты масштаба 1:25 000 на 4 части Границами листов десятитысячной карты будут меридианы, проведённые через 0º03’45”, и параллели проведённые через 0º02’30”. Десятитысячные листы обозначаются арабскими цифрами (1, 2, 3, 4).


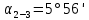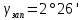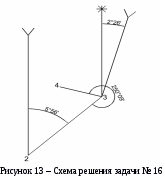
Задача № 16. Дирекционный угол лини 2-3 , сближение меридианов западное , угол правый, по ходу лежащий при точке 3 равен 250°09'. Вычислить истинный (географический) румб линии 3-4 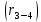. Решение сопроводить схемой.

Решение:






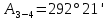
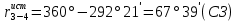
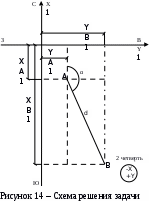
Задача № 28. Даны прямоугольные зональные координаты точек А и В: 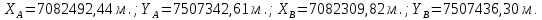Решить обратную геодезическую задачу, то есть вычислить длину линии АВ и её дирекционный угол. Решение сопроводить схемой.

Решение:

Вычисляем приращение координат:





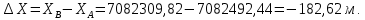
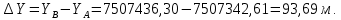
Определяем румб линии AB



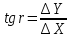
откуда



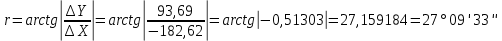
По знакам приращений координат(ΔX, ΔX), пользуясь таблицей связи румбов и дирекционных углов (Таблица 1), определяем, что вычисленное значение находится в 2 четверти и румб линии AB равен

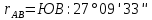
Таблица 1 - Связь румбов и дирекционных углов

Четверть	Значение дирекционного угла	Название румба	Связь между румбами и дирекционными углами	Знаки приращения координат
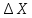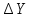1		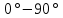СВ		+	+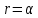
2		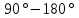ЮВ		-	+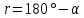
3		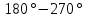ЮЗ		-	-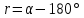
4		СЗ		+	-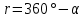

---

Для 2 четверти, пользуясь таблицей, определяем, что румб находится по формуле:



откуда





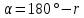
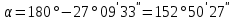
Определяем горизонтальное проложение линии AB

---

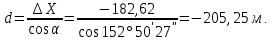
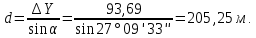
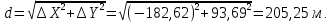
1.3. Обработка материалов теодолитной и тахеометрической съёмок

1.3.1 Вычисление координат пунктов замкнутого теодолитного хода

Из ведомости результатов измерения горизонтальных углов и расстояний в ведомость вычисления координат (таблица 2) выписывают значения горизонтальных углов замкнутого хода и средних горизонтальных проложений сторон теодолитного хода соответственно в графы 2 и 7. В графу 5 записывают измеренный дирекционный угол линии п.п. 35 – п.п. 36 .

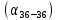Для сторон теодолитного хода, имеющих наклон к горизонтальной плоскости более 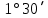, вычисляют горизонтальное проложение по формуле

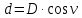(1.1)

где, 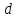- горизонтальное проложение стороны теодолитного хода, м;

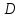- результат измерения длины стороны, м;

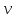- угол наклона линии к горизонтальной плоскости.

Вычисляют угловую невязку 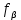замкнутого теодолитного хода

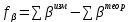(1.2)

где, 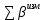- сумма измеренных углов;

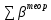- теоретическая сумма внутренних углов замкнутого теодо­литного хода,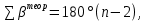



где n- число углов теодолитного хода.

Сравнивают найденную угловую невязку 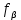с предельно допусти­мой невязкой 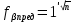. Если угловая невязка

---

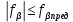допустима, то есть , то её распределяют в виде поправок 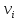с обратным знаком поровну во все измеренные углы (значения поправок 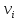при этом округляют до 0,1'):

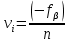(1.3)

Однако часто полученная невязка не делится на число углов без ос­татка. В этом случае большее значение поправки вводят в углы, образо­ванные короткими сторонами.

Сумма поправок, вводимых во все углы замкнутого теодолитного хода, должна равняться невязке с противоположным знаком: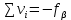

Вычисляют исправленные углы. Для этого к измеренному углу прибавляют поправку с учётом её знака:

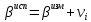(1.4)

Проверяют равенство суммы исправленных углов и теоретической суммы углов замкнутого хода , что позволяет проконтролировать правильность увязки углов.

Вычисляют дирекционные углы сторон привязочного и замкнутого теодолитных ходов по дирекционному углу исходной стороны п.п.35 - п.п.36 и исправленным углам :

,

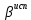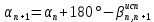(1.5)

где – дирекционный угол последующей стороны;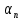

– дирекционный угол предыдущей стороны;

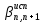- исправленный угол, вправо по ходу лежащий между предыдущей и последующей сторонами.

---