Файл: Лабораторная работа 4 Решение типовых задач алгебры и анализа студент гр. Сула255ск силин И. П.docx

ФИЛИАЛ ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮЖДЕТНОГО

ОБРАЗОВАТЕЛЬНО УЧРЕЖДЕНИЯ ВЫСШЕГО ОБРАЗОВАНИЯ

«УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫХ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» В Г. КУМЕРТАУ


Лабораторная работа №4

«Решение типовых задач алгебры и анализа»

Выполнил: студент гр.

СУЛА-255СК

Силин И.П.

Проверил: ст. пр.

кафедры ЭЛИ

Тузбеков Р.М.
Кумертау 2022

Оглавление

1. Задачи линейной алгебры

В системе MATLAB для решения довольно сложной задачи линейной алгебры – нахождение корней систем линейных уравнений – предусмотрены знаки операций / и \. Чтобы решить систему линейных уравнений:

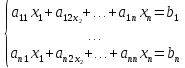
которую обычно кратко записывают в виде: Ax = B

Операция \, как уже было сказано в первой лекции, называется левым делением матриц и, будучи примененная к матрицам A и B в виде A\B, эквивалентна вычислению выражения inv(A)*B. Здесь под inv(A) понимается вычисление матрицы, обратной к матрице A (см. рис. 1)



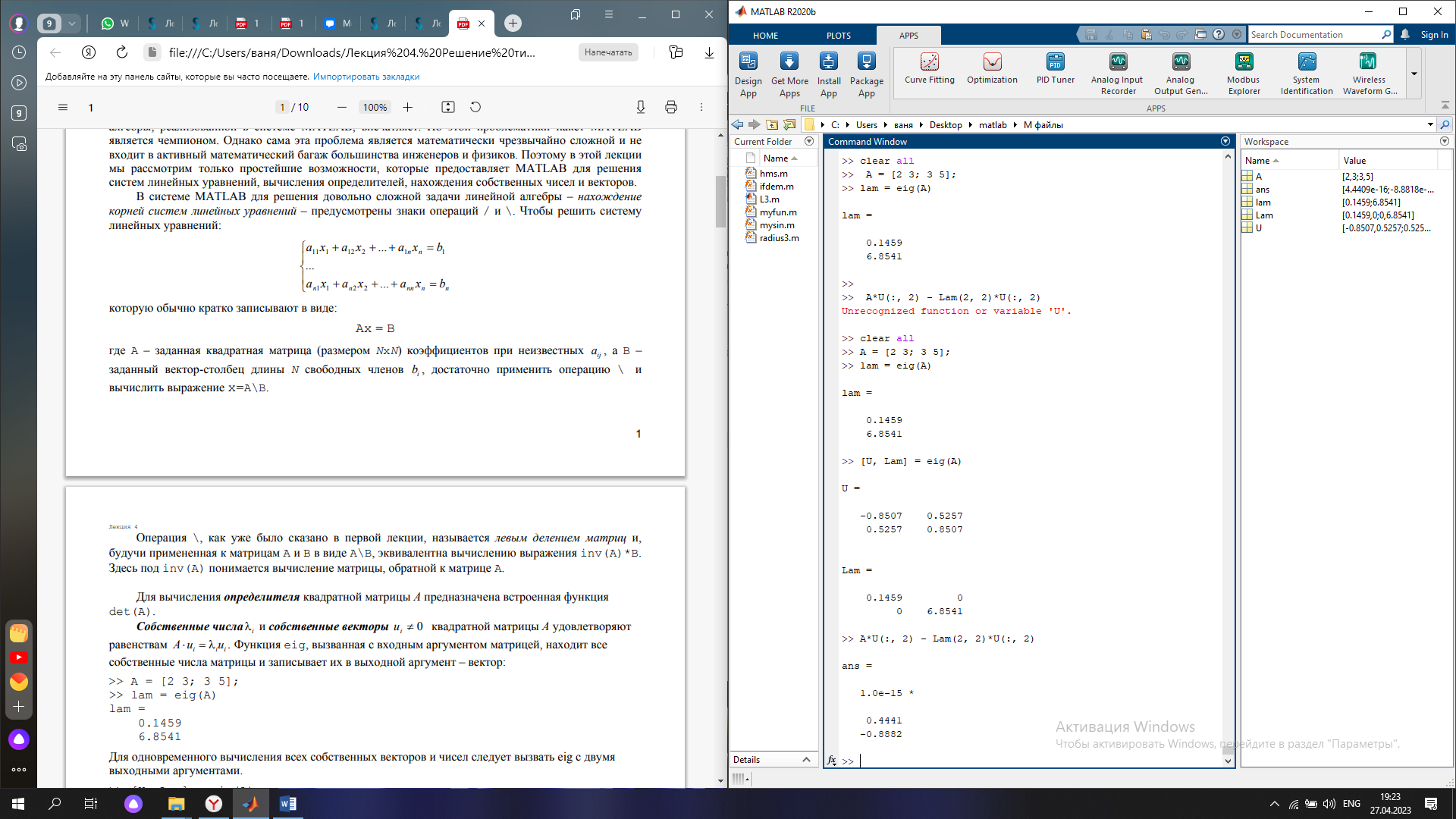
Рис. 1 Вычисление всех собственных векторов

2. Нахождение нулей функции

Решим, например, на отрезке [-5, 5] уравнение:

sin(x)-x^2.cos(x)=0. Перед нахождением корней полезно построить график функции, входящей в левую часть уравнения. Для получения графика можно прибегнуть к plot, но все равно понадобится. Поэтому имеет смысл воспользоваться fplot, которая к тому же позволяет получить более точный график по сравнению с plot (см. рис. 2)

---

Корень вблизи x=5

Корень вблизи x=-5

Корень вблизи x=-2


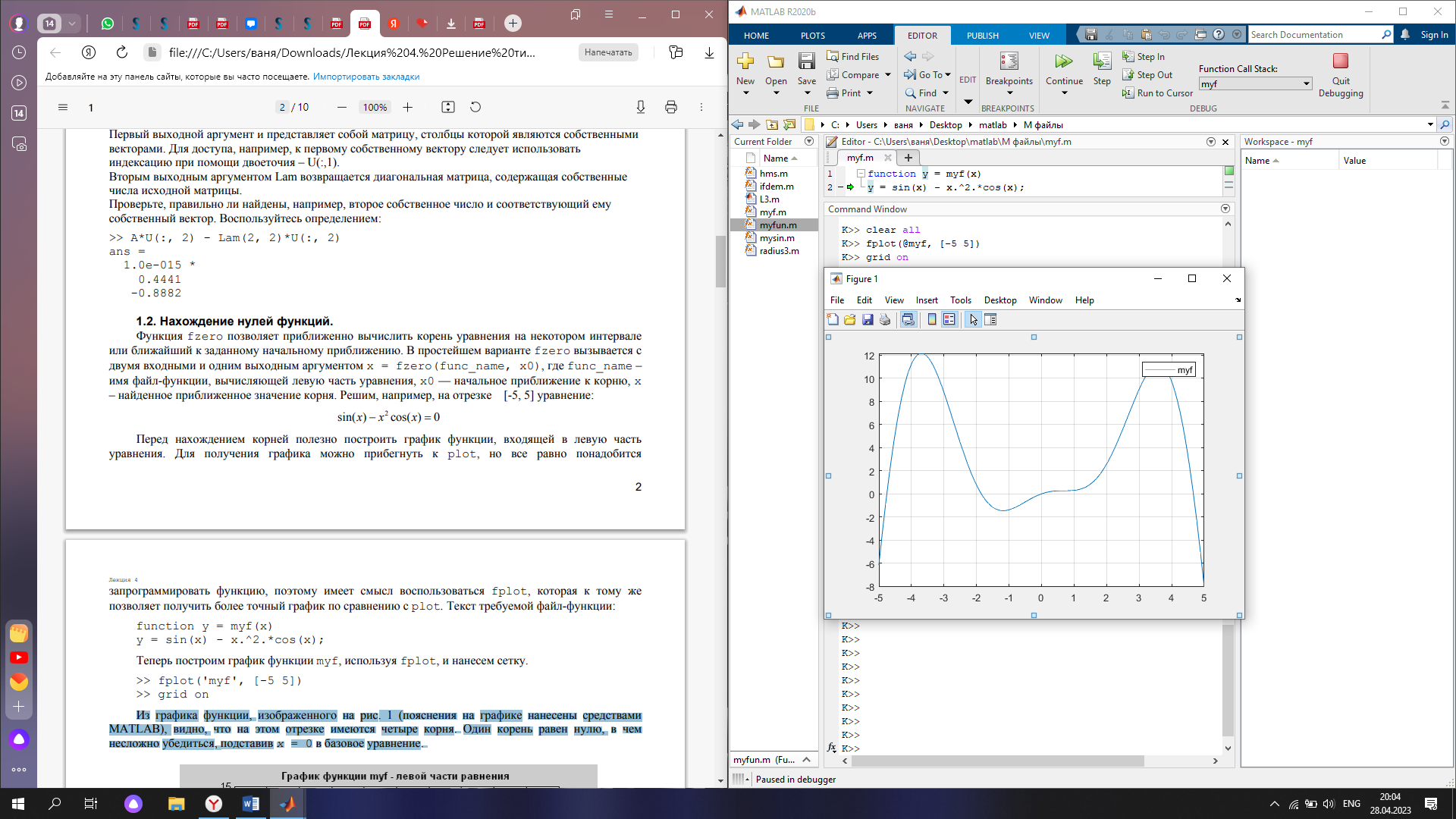
Рис. 2 график функции myf
Уточним значение корня, расположенного вблизи х=-5 при помощи fzero. Проверим ответ, вычислив значение функции myf в точке x1 (см. рис. 3).



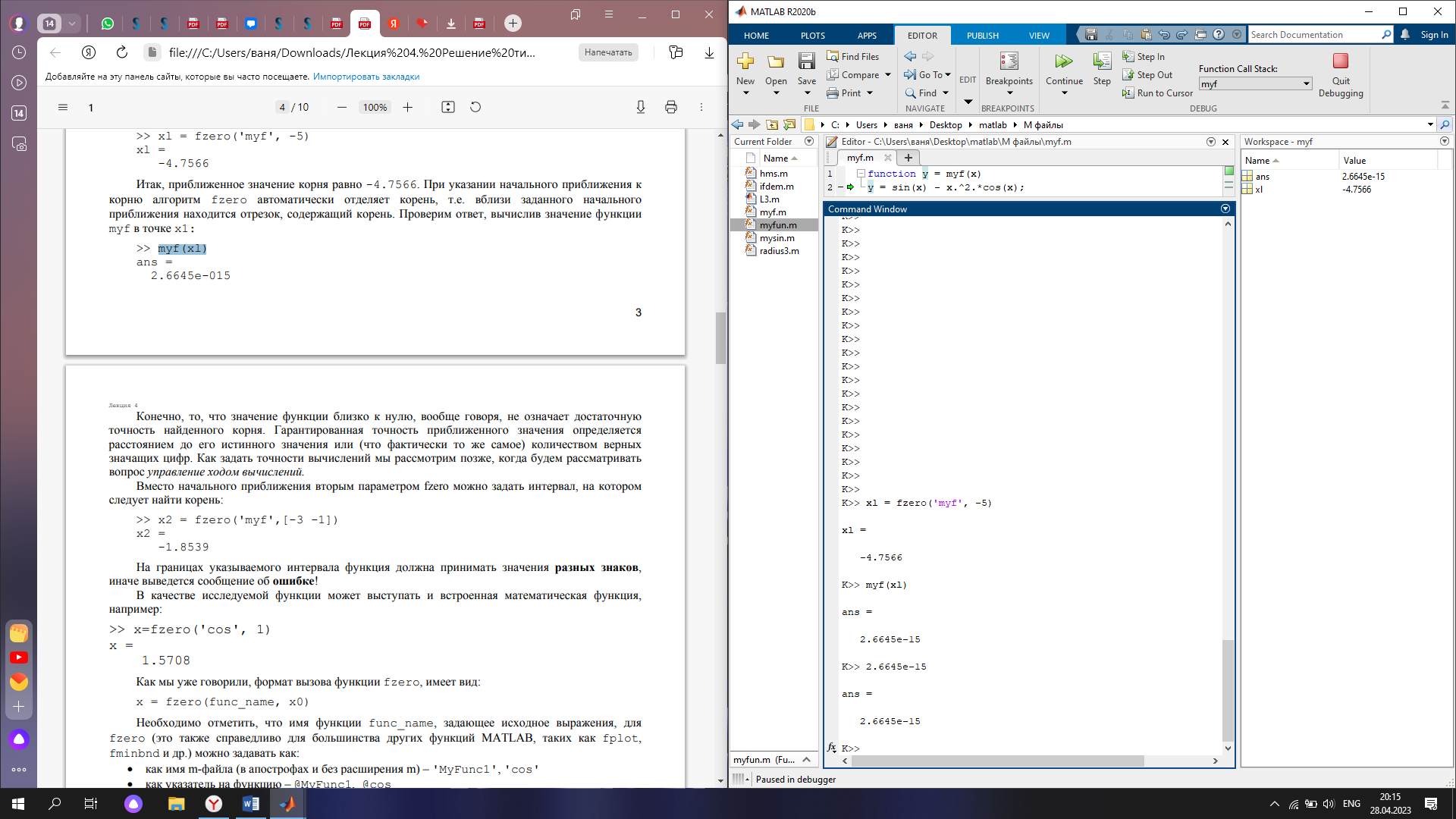
Рис. 3 нахождение приблизительного значения корня
Конечно, то, что значение функции близко к нулю, вообще говоря, не означает достаточную точность найденного корня. Гарантированная точность приближенного значения определяется расстоянием до его истинного значения или (что фактически то же самое) количеством верных значащих цифр (см. рис. 4)


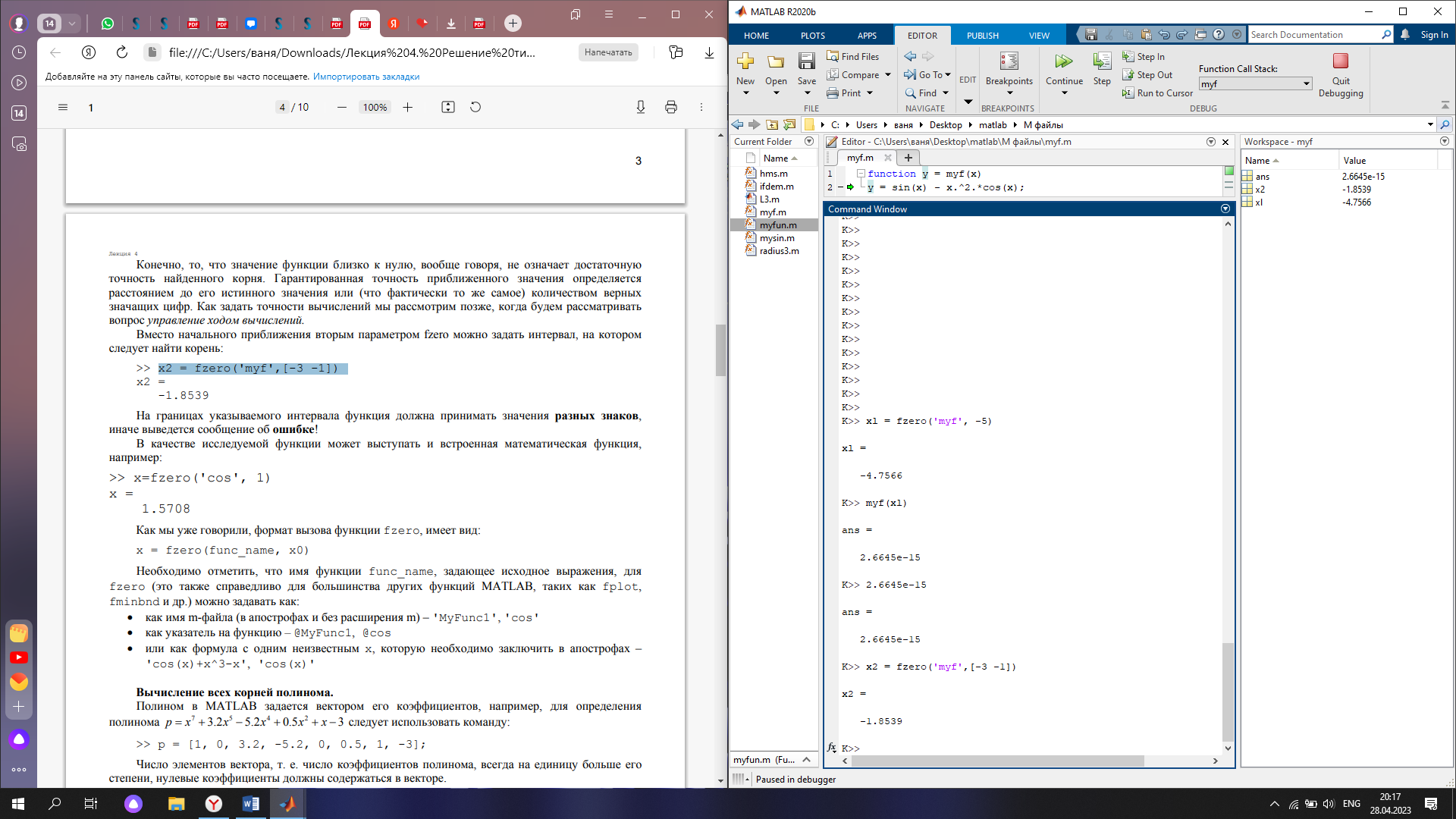
Рис. 4 Гарантированная точность приближенного вычисления

3. Вычисление корней полинома

Полином в MATLAB задается вектором его коэффициентов, например, для определения полинома p x⁷  3.2x⁵  5.2x⁴  0.5x²  x 3 следует использовать команду:

>> p = [1, 0, 3.2, -5.2, 0, 0.5, 1, -3];

Функция polyval предназначена для вычисления значения полинома от некоторого аргумента (см. рис. 5)


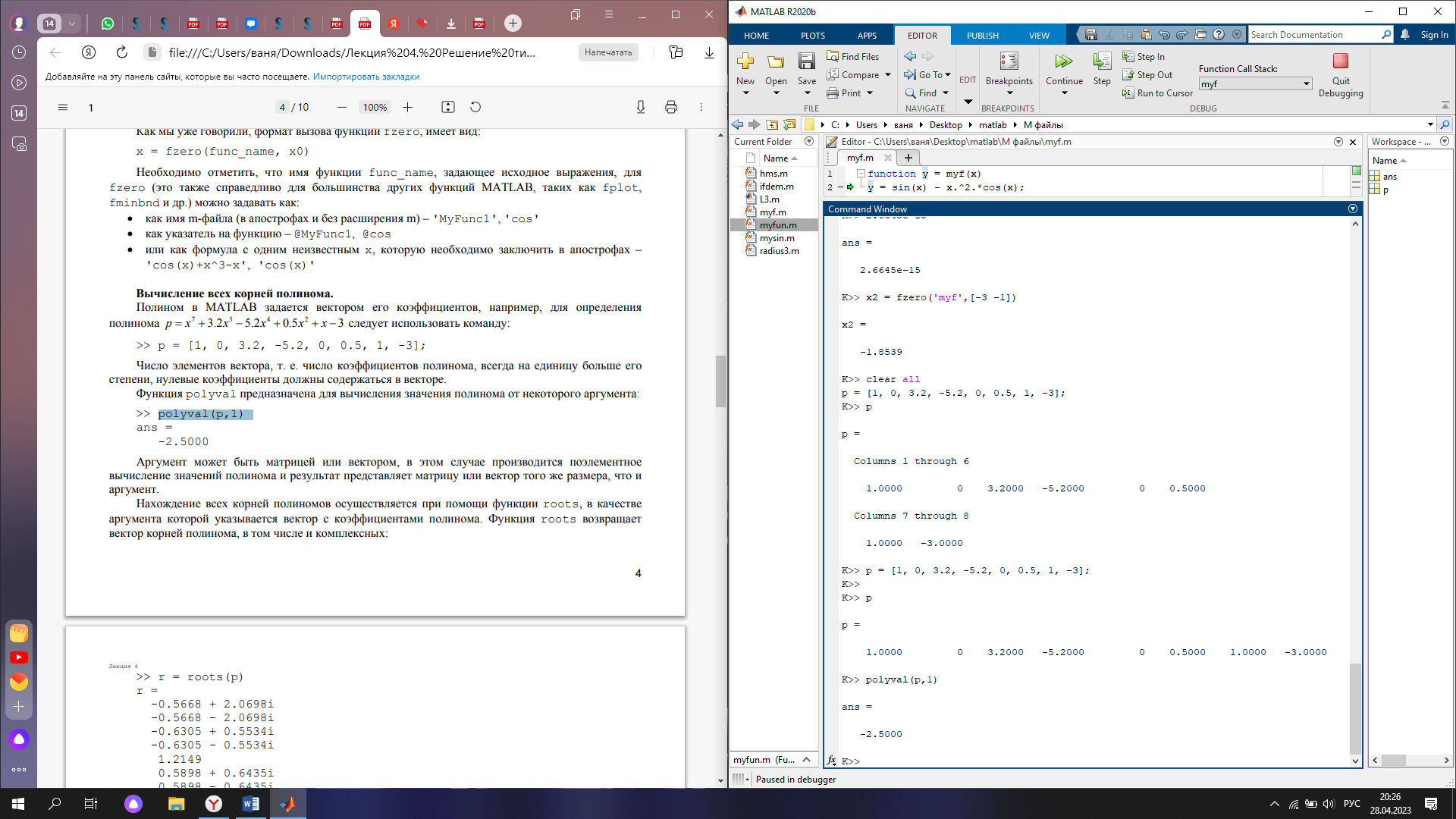
Рис. 5 Вычисление значения полинома от некоторого аргумента
Нахождение всех корней полиномов осуществляется при помощи функции roots, в качестве аргумента которой указывается вектор с коэффициентами полинома. Функция roots возвращает вектор корней полинома, в том числе и комплексных (см. рис. 6)


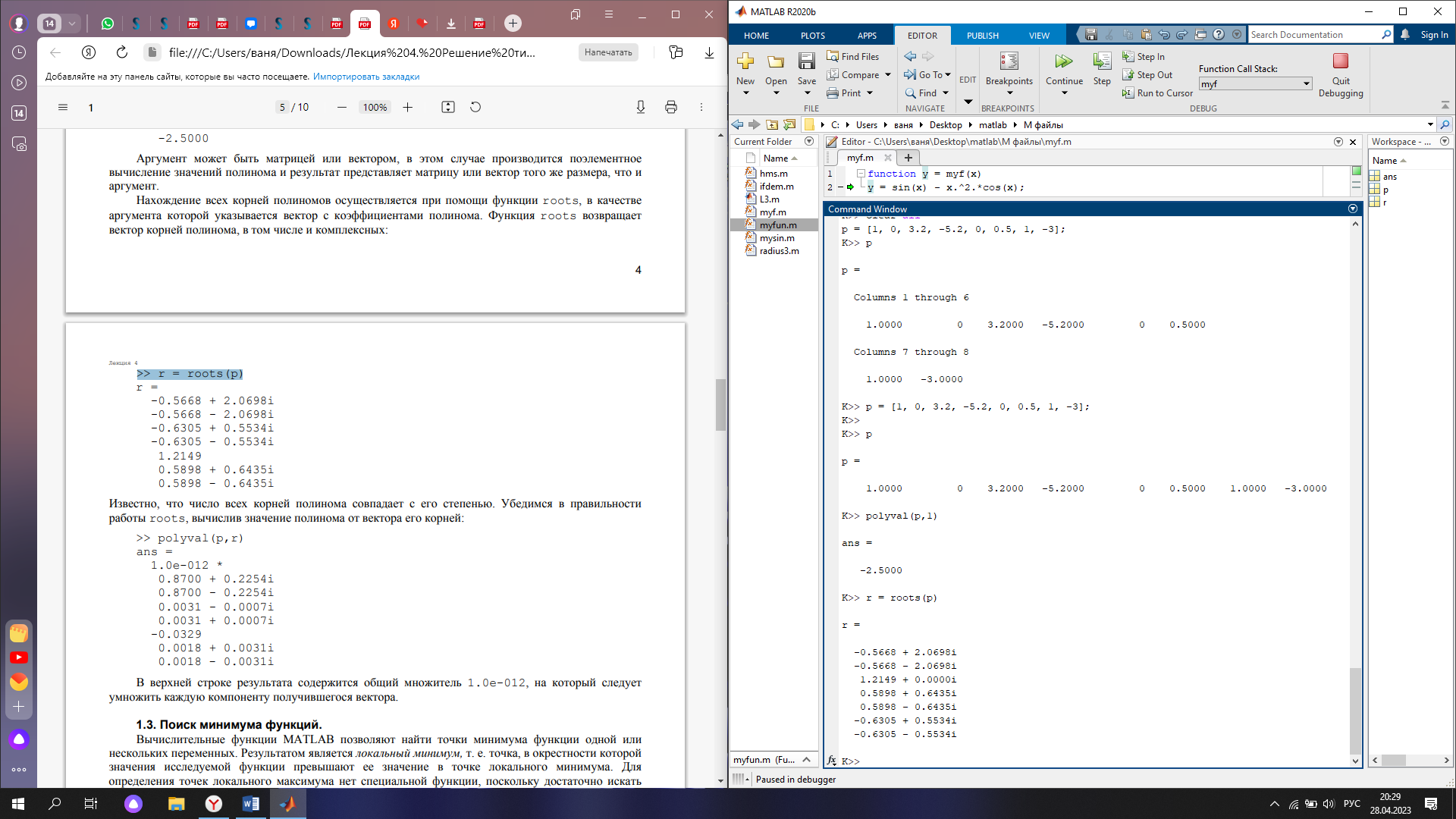
Рис. 5. Нахождение всех корней полинома
Известно, что число всех корней полинома совпадает с его степенью. Убедимся в правильности работы roots, вычислив значение полинома от вектора его корней (см. рис. 6)

---

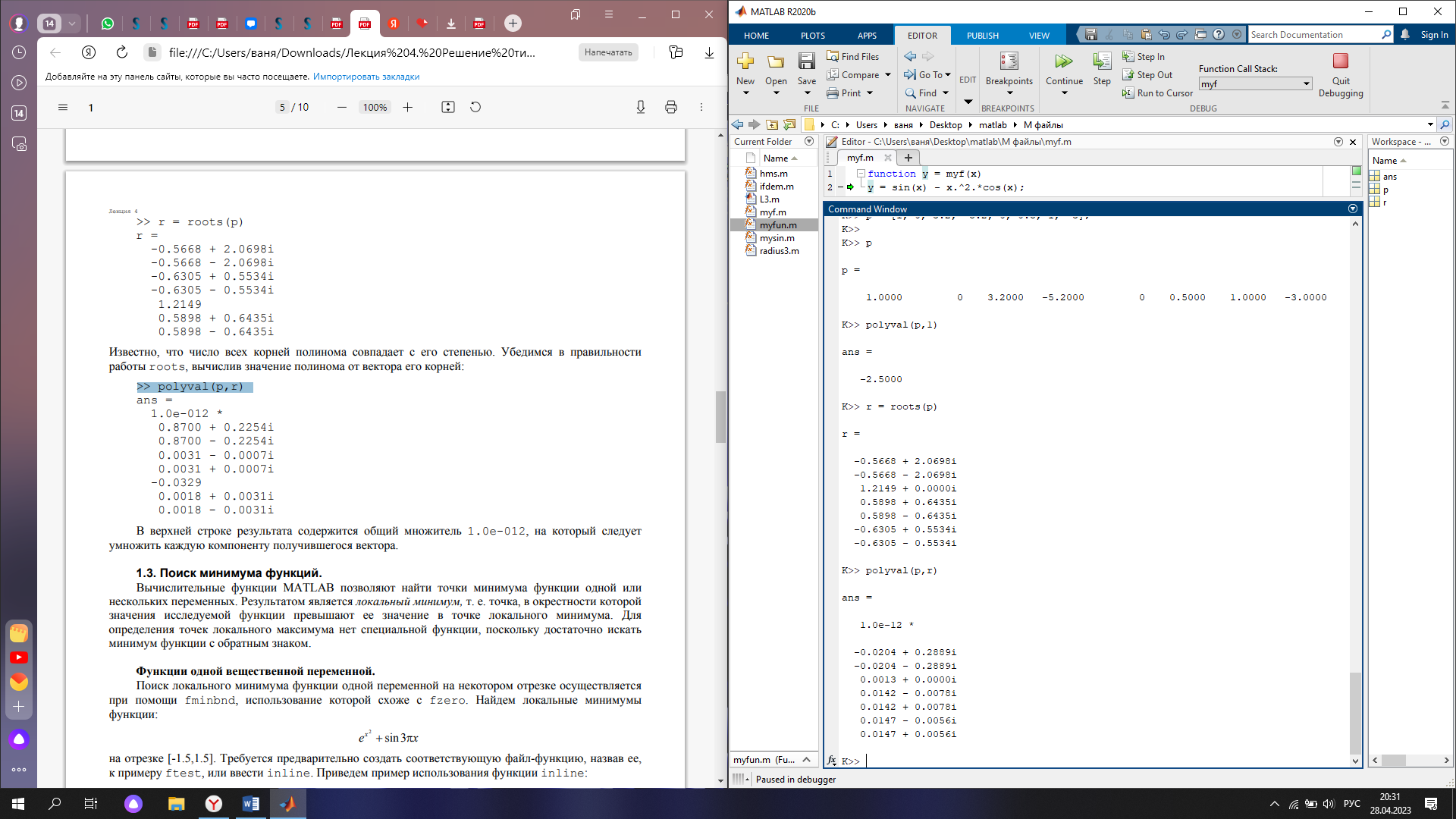
Рис. 6 Проверка правильности работы roots
Поиск локального минимума функции одной переменной на некотором отрезке осуществляется при помощи fminbnd, использование которой схоже с fzero. Найдем локальные минимумы функции: e^x2 sin 3x. Перед нахождением локальных минимумов нам необходимо исследовать поведение функции ftest на заданном отрезке. Для этого построим график исследуемой функции командой fplot (см. рис. 7). Обратите внимание, что для inline-функций апострофы применять не надо. Кроме того, использованием символа @ перед inline-функций также приведет к ошибке. Из графика, приведенного на рис.7, видно, что исследуемая функция имеет четыре локальных минимума.
Вычислим значение х, при котором достигается второй локальный минимум, задав первым аргументом fminbnd имя файл-функции или указатель на нее, а вторым и третьим – границы отрезка, на котором ищется локальный минимум.

---