Файл: Курсовая работа по дисциплине Теория электрической связи.docx
Добавлен: 30.11.2023
Просмотров: 103
Скачиваний: 7
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
Федеральное государственное бюджетное учреждение высшего образования
«САНКТ-ПЕТЕРБУРГСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ
Им. проф. М.А. БОНЧ-БРУЕВИЧА»
Кафедра теоретических основ телекоммуникаций
Курсовая работа
по дисциплине «Теория электрической связи»
Расчет основных характеристик цифровой системы связи с использованием квадратурной модуляции
Вариант № 86
Выполнил: Божок А. А.
Номер зачетной книжки: 2105086
Факультет: ИКСС
Направление: 11.03.02
Группа: ИКТЗ-15
Проверил: Виноградов В. Б.
Руководитель доцент кафедры
ТОТ,.
Оценка __________(подпись)
Санкт-Петербург
2023 г.
ОГЛАВЛЕНИЕ
Введение 3
Структурная схема системы цифровой связи 4
Исходные данные 5
Расчёт основных характеристик системы передачи цифровой информации 6
3.1. Источник сообщения 6
3.2. Аналого-цифровой преобразователь 11
3.3. Кодер 12
Введение
Данная курсовая работа посвящена современным цифровым системам связи и ориентирована на использование новых теоретических и практических достижений в области цифровой связи.
Цель курсовой работы:
-
Рассчитать основные характеристики случайных сигналов на выходе источника сообщений, на выходе АЦП, использовать свёрточное кодирование и декодирование на основе алгоритма Витерби. -
Применить современные виды модуляции (квадратурная амплитудная или квадратурная фазовая) с использованием соответствующих сигнальных созвездий. -
Рассмотреть определения вероятностных характеристик случайных процессов на выходах соответствующих функциональных узлов (корреляционные функции и спектральные плотности мощности). -
Обосновать каноническую форму сигналов квадратурных видов модуляции и определить корреляционную функцию на выходах СФФ, перемножителей в составе модулятора. -
Построить графики сигналов на выходе квадратурных модуляторов и на входе блока ФМС. -
Обосновать структурных схем квадратурных демодуляторов и определить вероятности ошибок на выходах решающих устройств (РУ) с последующим перерасчетом вероятности ошибок на выходе преобразователя параллельного кода в последовательный код. -
Исправить возможные ошибки на выходе демодулятора с использованием декодирования на основе алгоритма Витерби. -
Определить вероятности ошибок на выходе демодулятора при использовании квадратурных видов модуляции.
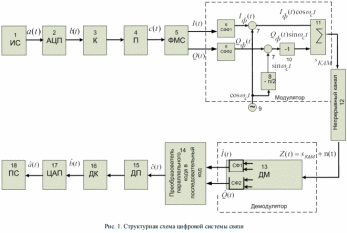 Структурная схема системы цифровой связи
Структурная схема системы цифровой связи
Назначение функциональных узлов системы цифровой связи:
1 – источник сообщений;
2 – аналого-цифровой преобразователь (АЦП);
3 – кодер (К); 4 – перемежитель (П);
5 – формирователь модулирующих символов (ФМС) или преобразователь последовательного кода в параллельный код;
6 – сглаживающие формирующие фильтры (СФФ1, СФФ2);
7 – перемножители;
8 – фазовращатель;
9 – генератор гармонических колебаний;
10 – инвертор;
11 – сумматор;
12 – непрерывный канал;
13 – демодулятор (ДМ);
14 – преобразователь параллельного кода в последовательный код;
15 – деперемежитель (ДП);
16 – декодер (ДК);
17 – цифро-аналоговый преобразователь (ЦАП);
18 – получатель сообщений.
Исходные данные
Таблица 1
| Параметр | Значение параметра | Данные по вашему варианту |
| Предельные уровни аналогового сигнала aмин, aмакс (В) | aмакс 25,6 В | aмакс 25,6 В |
| aмин 25,6 В | aмин = 25,6 В | |
| Верхняя частота спектра аналогового сигнала fв | fв 1 m102 104 Гц | fв 18600 Гц |
| Заданный уровень квантования | j 500 3 m | j 242 |
| Спектральная плотность мощности флуктуационной помехи | Номер варианта m, в пределах | N0 86 B2Гц |
| 67…99 | 1,85107 | |
| q– номер тактового интервала ошибки | q m(mod 3) 1 | q 3 |
| № вида модуляции l m(mod 2) | Вид модуляции | Вид модуляции по числу l |
| 0 | КФМ-4 | КФМ-4 |
Расчёт основных характеристик системы передачи цифровой информации
3.1. Источник сообщения
Источник сообщения (ИС) вырабатывает реализации a(t) стационарного случайного процесса A(t) типа квазибелого шума с параметрами амин, амакс и fв. Мгновенные значения сообщения равновероятны в интервале от значения амин до значения амакс.
1) Определение плотности вероятности.
Для определения плотности вероятности w(a) сигнала A(t) (сообщения A(t)) любая плотность вероятности должна удовлетворять условию нормировки:
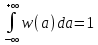
которое показывает, что площадь ограничения кривой w(a) от а =
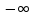 до а =
до а = 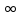 будет равна единице.
будет равна единице.Условие равновероятности мгновенных значений сообщения A(t) в интервале (амин, амакс) означает, что функция w(a) является равномерной, т. е. равна постоянной величине С в интервале (амин ‒ амакс), а вне указанного интервала равна нулю.
В данном случае условие нормировки примет вид С * (амин ‒ амакс) = 1, откуда
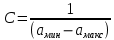 ;
; 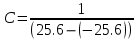 = 0.01953125(1/В).
= 0.01953125(1/В).Аналитическое выражение плотности вероятности w(a) будет равно:
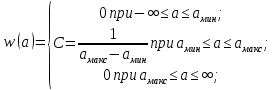
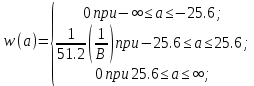
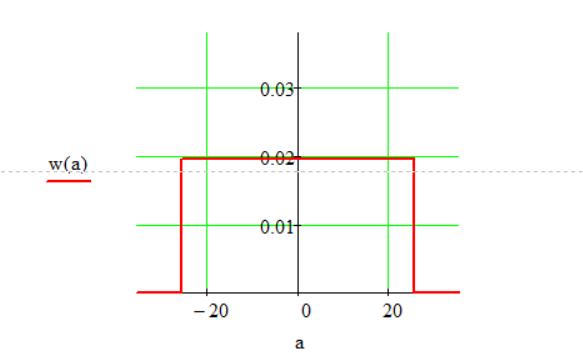
Рис. 2. График плотности вероятности w(a)
Определение функции распределения вероятности F(a)
Функция F(a) связана с плотностью вероятности w(a) интегральным равенством
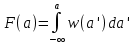
Выражение для функции распределения вероятности F(a) будет равно:
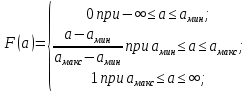
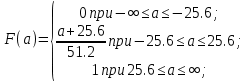
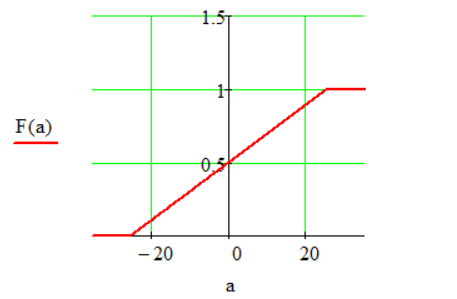
Рис. 3. График функции распределения
2) Расчёт математического ожидания и дисперсии сообщения.
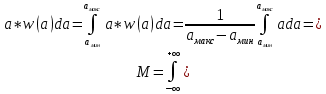
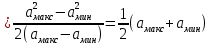
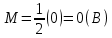
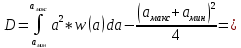
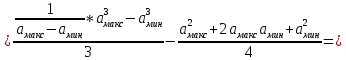
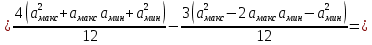
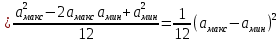 =
= 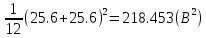 .
.3) Аналитическое выражение для спектральной плотности сообщения.
Сообщение A(t) является случайным процессом типа квазибелого шума, и его спектральная плотность мощности
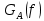 постоянна на частотном интервале от значения (
постоянна на частотном интервале от значения (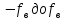 ), а вне этого интервала равна нулю. Обозначим значение функции
), а вне этого интервала равна нулю. Обозначим значение функции 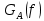 на интервале (
на интервале (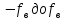 ) через
) через 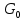 .
. Односторонняя спектральная плотность
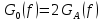 постоянна (равномерна) на частотном интервале от значения 0 до
постоянна (равномерна) на частотном интервале от значения 0 до 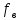 , а вне этого интервала равна нулю.
, а вне этого интервала равна нулю.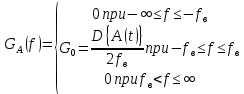
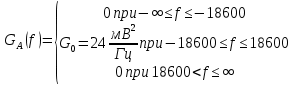
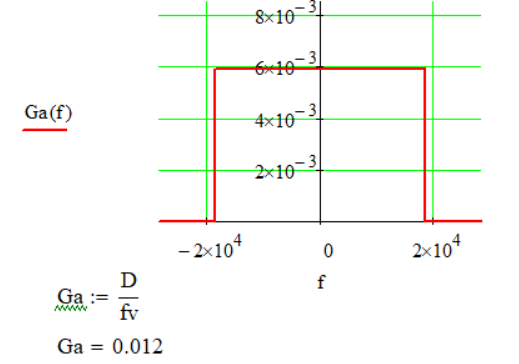
Рис. 4. График спектральной плотности мощности
4) Аналитическое выражение для корреляционной функции.
В соответствии с теоремой Винера – Хинчина корреляционная функция
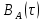 стационарного случайного процесса A(t) определяется следующей формулой:
стационарного случайного процесса A(t) определяется следующей формулой: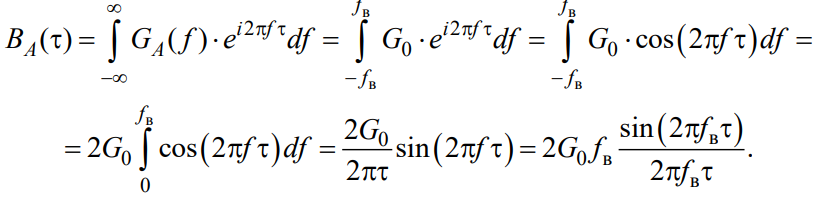
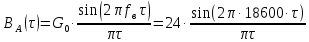



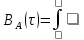

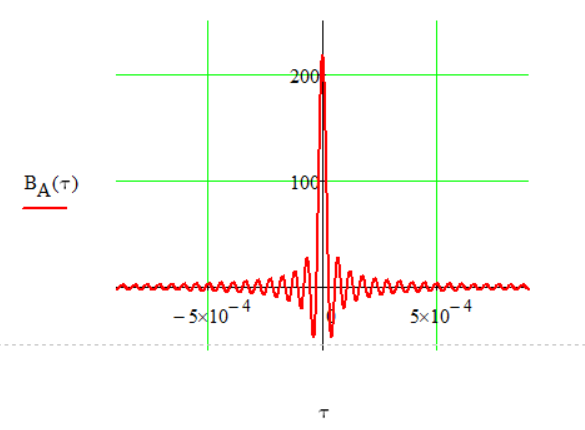
Рис. 5. График функции стационарного случайного процесса
3.2. Аналого-цифровой преобразователь
Аналого-цифровой преобразователь (АЦП) преобразует реализации аналогового (непрерывного) сообщения A(t) в цифровую форму, в поток двоичных символов: нулей и единиц, т. е. в последовательность прямоугольных импульсов, где «0» имеет нулевое напряжение, а «1» – прямоугольный импульс положительной полярности. Амплитуда импульсов U равна 1 В.
1. Расчет интервала дискретизации t для получения непрерывных отсчетов а(ti) реализации a(t):
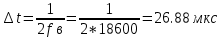
2. Расчет частоты дискретизации fд:
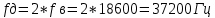
3. Определение числа уровней квантования:
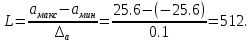
4. Расчет мощности шума квантования Ршк и мощности непрерывного сообщения:
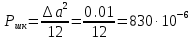 В2
В2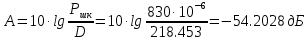
5. Минимальное число двоичных разрядов k, требуемое для записи в двоичной форме номера j (k – целое число):
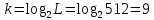
6. Перевод заданного уровня квантования j в двоичную форму: