Файл: Приближенное вычисление определённых интегралов.docx

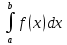, где f (x) есть некоторая заданная на промежутке [a, b] непрерывная функция. Если F(x) есть какая-либо первообразная от непрерывной функции f(x), то справедлива формула

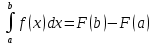– формула Ньютона – Лейбница.

Всякая функция f(x),непрерывная на интервале (a, b) имеет на этом интервале первообразную, т.е. существует такая функция F(x), что F'(x) = f(x). Однако не всякая первообразная, даже тогда, когда она существует, выражается в конечном виде через элементарные функции. Например первообразные, выраженные интегралами:

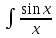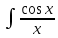dx,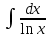

. Во всех подобных случаях первообразная представляет собой некоторую новую функцию, которая не сводится к комбинации конечного числа элементарных функций. В случаях, когда первообразная для функции f(x) не вычисляется, а также, если функция f(x) на промежутке [a, b] задана таблично или графически, то применить формулу Ньютона – Лейбница нельзя. В этих случаях применяются различные методы приближенного вычисления определенных интегралов.
Ф 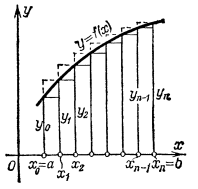ормула прямоугольников

. Пусть на промежутке [a, b] задана непрерывная функция

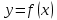. Требуется вычислить определенный интеграл

. Разделим промежуток [a, b] точками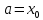

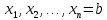на n равных частей длины △x :

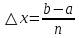. Обозначим далее через

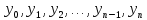значения функции f(x) в точках

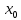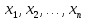, т.е.

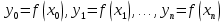. Составим суммы:

;

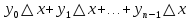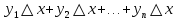. Каждая из этих сумм является интегральной суммой для f(x) на промежутке [a, b] и поэтому приближенно выражает интеграл:

.

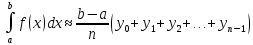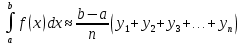Это и будут формулы прямоугольников. Ошибка, совершаемая при вычислении интеграла по формуле прямоугольников, будет тем меньше, чем больше число n( т.е. чем меньше шаг деления

).
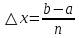Формула трапеций. Более точное значение определенного интеграла мы получим если данную кривую

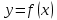заменим не ступенчатой линией, как это было в методе прямоугольников, а вписанной ломаной. Тогда площадь

к

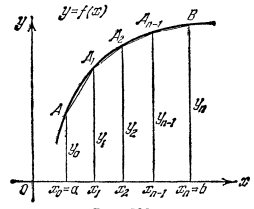риволинейной трапеции aABb заменится суммой лощадей прямолинейных трапеций, ограниченных сверху хордами

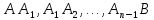. Площадь первой из этих трапеций равна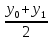

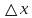, площадь второй равна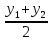

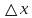и т.д., то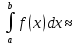

+ … +

) =

(

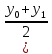
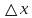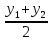
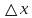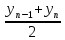
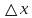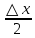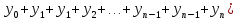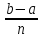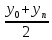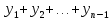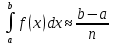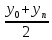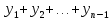) – формула трапеций.

Чем больше число n, тем точнее сумма, написанная в правой части приближенного равенства, будет давать значение интеграла.

Формула парабол (формула Симпсона). Разделим промежуток [a, b] на четное число равных частей

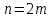. Площадь криволинейной трапеции, соответствующей первым двум промежуткам

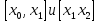и ограниченной заданной кривой

заменим площадью криволинейной трапеции, которая ограничена параболой второй степени, проходящей через три точки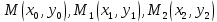

и имеющей ось, параллельную оси

OY. Такая криволинейная трапеция называется параболической трапецией.

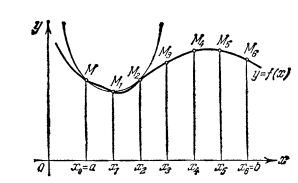
Уравнение параболы с осью, параллельной оси OY, имеет вид

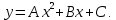Коэффициенты A, B, C однозначно определяются из условия, что парабола проходит через три заданные точки. Аналогичные параболы строятся и для других пар промежутков. Сумма площадей параболических трапеций и даст приближенное значение интеграла.

Если криволинейная трапеция ограничена параболой

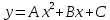, осью ОХ и двумя ординатами, расстояние между которыми равно 2h, то ее площадь равна:

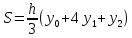, где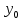

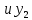– крайние ординаты, а

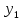ордината кривой в середине отрезка. Тогда (h =

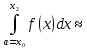
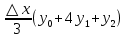; складывая все промежутки получим:

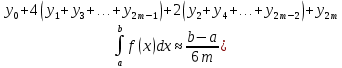] – формула Симпсона.

Число точек деления 2m произвольно, но чем больше это число, тем точнее сумма в правой части равенства дает значение интеграла.