Добавлен: 03.12.2023
Просмотров: 71
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство образования Российской Федерации
Санкт-Петербургский Государственный Горный Институт им. Г.В. Плеханова
(технический университет)
Отчёт по лабораторной работе № 2.
По дисциплине: Физика
(наименование учебной дисциплины согласно учебному плану)
Тема: Оценка точности прямых и косвенных измерений.
Выполнил: студент гр. АПМ-03 ___________ / Сафонов Д.Н. /
(подпись) (Ф.И.О.)
ОЦЕНКА: _____________
Дата: __________________
ПРОВЕРИЛ:
Ассистент: ____________ / Стоянова Т.В./
(подпись) (Ф.И.О.)
Санкт-Петербург
2004 год.
Цель работы
Обработать данные прямых и косвенных измерений физических величин.
Краткие теоретические сведения
Определения основных физических понятий, объектов, процессов и величин.
Прямое измерение — измерение, при котором искомое значение физической величины получают непосредственно.
Косвенное измерение — определение искомого значения физической величины на основании результатов прямых измерений других физических величин, функционально связанных с искомой величиной.
Случайная погрешность — погрешность, меняющаяся (по величине и по знаку) от измерения к измерению. Случайные погрешности могут быть связаны с несовершенством приборов (трение в механических приборах и т. п.), тряской в городских условиях, с несовершенством объекта измерений.
Систематическая погрешность — погрешность, изменяющаяся во времени по определенному закону. Систематические погрешности могут быть связаны с ошибками приборов (неправильная шкала, калибровка и т. п.), неучтёнными экспериментатором.
Погрешности прямых измерений:
-
Среднее значение:
Предположим, что мы проводим серию измерений величины Х. Из-за наличия случайных ошибок, получаем n различных значений: Х1, Х2… Хn
-
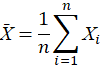
Абсолютная ошибка i – го измерения
называется разность между средним значением и результатом i – го измерения:
-
Относительная ошибка – служит для характеристики точности измерений, которую принято выражать в процентах
-
Систематическая погрешность прибора:
где К – класс точности прибора, Хпр – предельное значение величины, которое может быть измерено по шкале прибора.
-
Квадратичная погрешность:
При ответственных измерениях, когда необходимо знать надежность полученных результатов, используется средняя квадратичная ошибка (или стандартное отклонение), которая определяется формулой
Удельное электрическое сопротивление – это сопротивление однородного куска проводника длиной 1 м и площадью токоведущего сечения 1 м².
Характеризует его способность проводить электрический ток.
[R]=Oм - сопротивление проводника;
[S]=м*м – площадь поперечного сечения проводника
[l]=м – длина проводника
[ρ]= Ом·м
Сопротивление проводника с удельным сопротивлением ρ, длиной l и площадью сечения S может быть рассчитано по формуле:
Электрическое сопротивление — скалярная физическая величина, характеризующая свойства проводника и равная отношению напряжения на концах проводника к силе электрического тока, протекающему по нему.
где
R — сопротивление проводника;
[R]=Oм
U — разность электрических потенциалов на концах проводника
[U]=B
I — ток, протекающий между концами проводника под действием разности потенциалов
[I]=A
Законы и соотношения, описывающие изучаемые процессы, на основании которых, получены расчётные формулы. Пояснения к физическим величинам и их единицы измерений.
По закону Ома для участка цепи сила тока
, текущего по металлическому проводнику, прямо пропорциональна падению напряжения 
на этом проводнике и обратно пропорциональна сопротивлению проводника: 
,где
- сопротивление проводника, которое зависит от его формы, размеров и свойств материала из которого изготовлен проводник. 
,Удельное сопротивление
характеризует способность вещества проводить электрический ток и зависит от химической природы вещества и условий, в которых находится проводник. В системе СИ удельное сопротивление измеряется в 
.Измерение размеров проволоки следует проводить с помощью линейки или микрометра. Сила тока измеряется амперметром, а напряжение вольтметром.
Основные расчётные формулы.
Удельное сопротивление
,
;Поперечное сечение проводника
d – диаметр проводника [d]=
S – площадь поперечного сечения
Среднее значение диаметра проволоки
;Сопротивление проводника
, 
;Графическое вычисление
;Формулы погрешности.
При прямых измерениях:
Величина средней абсолютной ошибки диаметра
;Средняя квадратичная ошибка измерений диаметра
;Абсолютная погрешность прибора
;При косвенных измерениях:
Абсолютная погрешность
;Средняя квадратичная ошибка
;Абсолютная погрешность
;Средняя квадратичная ошибка
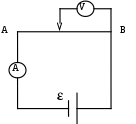
;Схема установки.
В
ольтметр
Вольтметр
Проводник
Амперметр
Источник тока
Таблица 1(а).
| Физическая величина |  |  |  |  |  |  |  |  |  |  |
| Ед. изм. Прибор | м  | м | м | м | м | м | м | м | м | м |
| Штангель- Циркуль | 0,30 | 0,30 | 0,30 | 0,30 | 0,29 | 0,25 | 0,25 | 0,30 | 0,30 | 0,30 |
| Микрометр | 0,30 | 0,29 | 0,29 | 0,30 | 0,26 | 0,27 | 0,26 | 0,29 | 0,29 | 0,30 |
Таблица 1(б).
| Физическая величина |  |  |  |  |  |
| Ед. изм. Прибор | м  | М | м |  | |
| Штангель- циркуль | 2,85 | 0,21 | 0,24 | 0,72 | 0,84 |
| Микрометр | 2,85 | 0,13 | 0,16 | 0,51 | 0,56 |
Таблица 2.
| Физическая величина |  |  |  |  |  |  |  |  |  |
| Ед. изм. № опыта | М  | м | А | А | В | В  | Ом | Ом | Ом |
| 1 | 5 | 0,5 | 100 | 3,73 | 0,10 | 2,3 | 1,0 | 0,41 | 0,29 |
| 2 | 10 | 0,5 | 100 | 3,73 | 0,15 | 2,3 | 1,5 | 0,41 | 0,29 |
| 3 | 15 | 0,5 | 100 | 3,73 | 0,20 | 2,3 | 2,0 | 0,41 | 0,29 |
| 4 | 20 | 0,5 | 100 | 3,73 | 0,35 | 2,3 | 3,5 | 0,41 | 0,29 |
| 5 | 25 | 0,5 | 100 | 3,73 | 0,45 | 2,3 | 4,5 | 0,41 | 0,29 |
| 6 | 30 | 0,5 | 100 | 3,73 | 0,50 | 2,3 | 5,0 | 0,41 | 0,29 |
| 7 | 35 | 0,5 | 100 | 3,73 | 0,65 | 2,3 | 6,5 | 0,41 | 0,29 |
| 8 | 40 | 0,5 | 100 | 3,73 | 0,70 | 2,3 | 7,0 | 0,41 | 0,29 |
| 9 | 45 | 0,5 | 100 | 3,73 | 0,75 | 2,3 | 7,5 | 0,41 | 0,29 |
| 10 | 50 | 0,5 | 100 | 3,73 | 0,85 | 2,3 | 8,5 | 0,41 | 0,29 |
Таблица 3.
| Физическая величина |  |  |  |  |
| Ед. изм. № опыта |  | |  | |
| 1 | 1,91 | 1,30 | 2,66 | 1,74 |
| 2 | 1,53 | 1,30 | 2,66 | 1,74 |
| 3 | 1,36 | 1,30 | 2,66 | 1,74 |
| 4 | 1,27 | 1,30 | 2,66 | 1,74 |
| 5 | 1,22 | 1,30 | 2,66 | 1,74 |
| 6 | 1,17 | 1,30 | 2,66 | 1,74 |
| 7 | 1,15 | 1,30 | 2,66 | 1,74 |
| 8 | 1,13 | 1,30 | 2,66 | 1,74 |
| 9 | 1,12 | 1,30 | 2,66 | 1,74 |
| 10 | 1,11 | 1,30 | 2,66 | 1,74 |
Примеры расчётов физических величин.
Примеры расчётов погрешностей.
; 
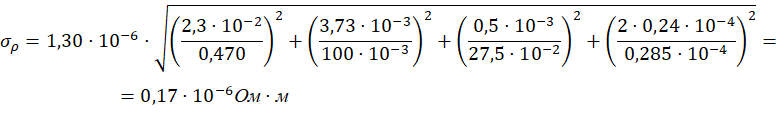
График зависимости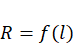 
.
Таблица данных для графика:
l, м | R, Ом |
0 | 0 |
0,05 | 1,0 |
0,1 | 1,5 |
0,15 | 2,0 |
0,2 | 3,5 |
0,25 | 4,5 |
0,3 | 5,0 |
0,35 | 6,5 |
0,4 | 7,0 |
0,45 | 7,5 |
0,5 | 8,5 |
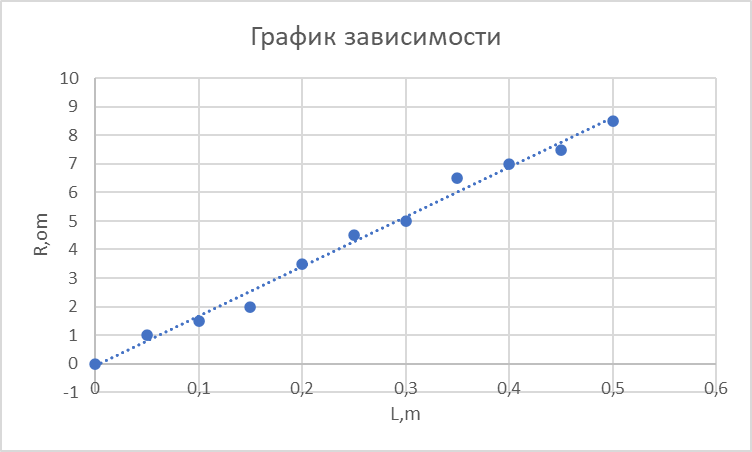
Среднее значение удельного сопротивления, вычисленное графически.
Имеем формулу
, где 
.Выберем из графика значения
для определения тангенса угла наклона прямой к оси 
.
Конечные результаты.
Итак, получены следующие результаты для удельного сопротивления:
И для диаметра проволоки:
Значение удельного сопротивления проволоки, вычисленное графически:
Вывод.
В ходе данной лабораторной работы были проделаны измерения и вычисления для определения значения удельного сопротивления проводника.
Полученная погрешность имеет небольшое значение, что даёт право говорить об отсутствии грубых ошибок при измерениях и вычислениях. Следуя из всего вышесказанного можно сделать вывод, что данный метод вычисления, при данных приборах можно использовать для определения удельного сопротивления.