Файл: Практическая задача на кредитоспособность клиента.pdf

,

где t – время;

xi и yj– соответственно выходное значение i-го и j-го нейронов.

В начальный момент времени предполагается, что:

Правило Хеббо для нейронной сети можно представить в виде выражений:

Аналогичным образом правило Хебба записывается для нейронной сети большей размерности. Правило Хебба может использоваться как при обучении с учителем, так и без него.

Правило обучения Розенблатта

Данную процедуру предложил американский ученый Розенблатт в 1959г. для нейронной сети, которую он назвал персептрон. Персептрон – это сеть, состоящая из S, A и R нейронных элементов. Нейроны слоя S называются сенсорными и предназначены для формирования входных сигналов в результате внешних воздействий. Нейроны слоя А называются ассоциативными и предназначены для непосредственной обработки входной информации. Нейроны слоя R называются эффекторными. Они служат для передачи сигналов возбуждения к соответствующему объекту, например к мышцам.

Таким образом, персептрон Розенблатта содержит один слой обрабатывающих нейронных элементов, в качестве которых используются нейронные элементы с пороговой функцией активации. Поэтому обучение персептрона происходит путем настройки весовых коэффициентов между слоями S и A.

Математическую формулировку правила обучения Розенблатта можно представить в следующем виде:

где tj – эталонное значение j-го выхода нейронной сети;

α – коэффициент, характеризующий скорость обучения сети.

Величина скорости обучения характеризуется следующими значениями: , 0 < α ≤ 1.

Процедура обучения Розенблатта состоит из следующих шагов:

1. Весовые коэффициенты W нейронной сети инициализируются случайным образом или устанавливаются в нулевое состояние.
2. На входы сети поочередно подаются входные образы X из обучающей выборки, которые трансформируются в выходные сигналы нейронных элементов Y.
3. Если реакция нейронной сети yj совпадает с эталонным значением tj, т.е. если yj=tj, то весовой коэффициент wij не изменяется.
4. Если выходная реакция сети yj не совпадает с эталонной, т.е. если yj ≠tj, то производится модификация весовых коэффициентов по правилу.
5. Шаги 2-4 повторяются до тех пор, пока не станет yj=tj, для всех входных образов, или не перестанут изменяться весовые коэффициенты.

Согласно теореме сходимости персептрона, алгоритм сходится за конечное число шагов, если существует решение задачи.

Правило обучения Видроу-Хоффа

Правило обучения Видроу-Хоффа известно под названием дельта-правило. Оно предполагает минимизацию среднеквадратичной ошибки нейронной сети, которая для L входных образов определяется следующим образом:

где E(k) – среднеквадратичная ошибка сети для k-го образа;

и – соответственно выходное и эталонное значение нейронной сети для k-го образа.

Среднеквадратичная ошибка нейронной сети для одного входного образа определяется по формуле:

.

Алгоритм обратного распространения ошибки

Алгоритм обратного распространения ошибки является одним из наиболее эффективных средств для обучения многослойных нейронных сетей. Алгоритм минимизирует среднеквадратичную ошибку сети. Для любого скрытого слоя i ошибка i-го нейронного элемента определяется рекурсивным образом через ошибки нейронов следующего слоя j:

,

где m – число нейронов следующего слоя по отношению к слою i;

– синаптическая связь между i-м и j-м нейронами различных слоев;

– взвешенная сумма j-го нейрона.

Производные среднеквадратичной ошибки по весовым коэффициентам и порогам нейронных элементов для любых двух слоев i и j многослойной сети определяются следующим образом:

Для минимизации среднеквадратичной ошибки сети весовые коэффициенты и пороги нейронных элементов должны изменяться с течением времени следующим образом:

где α – скорость обучения.

6. Практическая часть

В вычислительную среду MATLAB интегрированы десятки прикладных инженерных и математических программ, одним из них является Fuzzy Logic Toolbox. Пакет Fuzzy Logic Toolbox поддерживает все фазы разработки нечетких систем, включая синтез, исследование, проектирование, моделирование, и внедрение в режиме реального времени. Ключевыми особенностями Fuzzy Logic Toolbox являются:

• специализированные GOI-модули для создания нечеткого вывода;
• реализация популярных алгоритмов нечеткого вывода Мамданим и Сугено;
• библиотека функций принадлежности;
• настройка функций принадлежности ANFIS-алгоритмов;
• экстракция нечетких правил с помощью кластеризации данных;
• возможность внедрения систем вывода в Simulink через модуль «нечеткий контроллер»;
• Си-код алгоритмов нечеткого вывода, позволяющий использовать спроектированные нечеткие системы вне среды MATLAB.

Fuzzy Logic Toolbox включает следующие GUI-модули:

• Fuzzy Inference System Editor – редактор общих свойств системы нечеткого вывода. Позволяет установить количество входов и выходов системы, выбрать тип системы, реализации логических операций, в также вызвать другие GUI-модули.
• Membership Function Editor – редактор функций принадлежности. Выводит на экран графики функций принадлежности входных и выходных переменных. Позволяет задать тип и параметры функций принадлежности.
• Rule Editor – редактор нечеткой базы знаний. Поволяет создавать и редактировать правила, выбирая нужные сочетания.
• Rule Viewer – браузер нечеткого вывода. Графически показывает выполнение нечеткого вывода по каждому правилу.
• Surface Viewer – браузет поверхности «входы-выход» нечеткой системы. Выводит графики зависимости выходной переменной от любых двух входных переменных.

Задача на кредитоспособность клиента

В задаче требуется определить под какую % ставку банку можно предоставить кредит клиенту. Входные сигналы: а) кредитная история (хорошая, плохая); б) платежеспособность клиента (хорошая, средняя, плохая). Выходной сигнал: значение % ставки кредита для клиента (низкий %, средний %, высокий %). Правила: Если кредитная история хорошая, платежеспособность хорошая, то % ставка по кредиту низкий. Если кредитная история хорошая, платежеспособность средняя, то % ставка по кредиту средняя. Если кредитная история плохая, платежеспособность плохая, то % ставка по кредиту высокая.

Решение задачи

В строке функций MATLAB вводим «FUZZY» и нажимаем Enter. В открывшемся окне редактора создаем входы, выходы, функции принадлежности, можем редактировать и наблюдать за работой правил. В нашей задаче два входа: кредитная история и платежеспособность клиента.

С начала в окне отображен один вход. С помощью команды Edit→Add variable…→Input добавляем второй вход. Переименуем оба входа с помощью функции Name. Один назовем «кредитистория», второй – «платежеспособность».

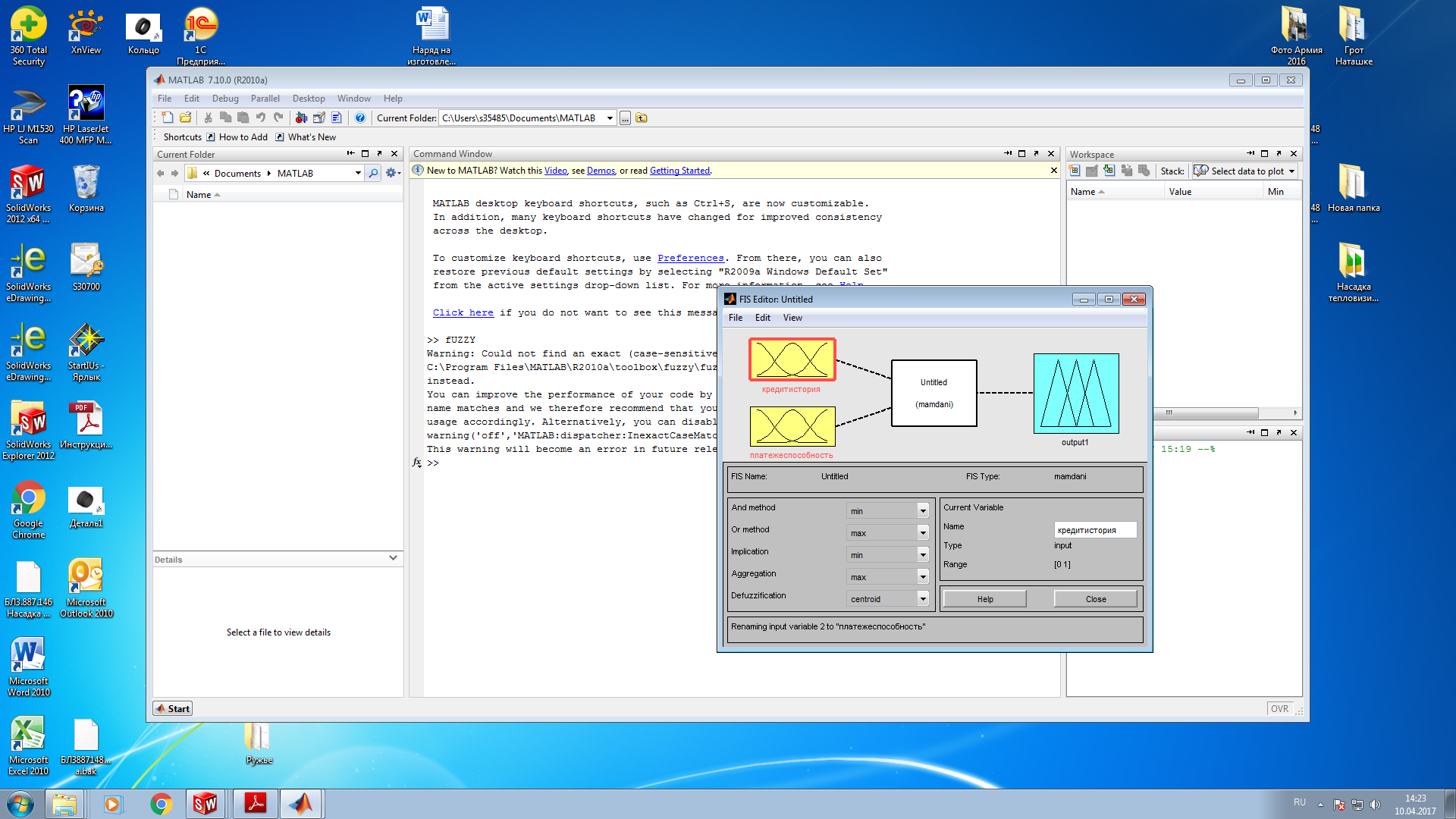
Рис.6

Так же у нас есть выходной блок системы. Переименуем его в «ставкакредита».

Рис.7

А также дадим имя нашей системе: «Newzadaca».

Рис.8

Далее нам необходимо задать функции принадлежности для входных блоков «кредитистория» и «платежеспособность». Выбираем пункт меню Edit→Add MFs… в появившемся окне Membership Function выбираем MF type и Number of MFs. Для входного блока «кредитистория» это будет тип gaussmf с общим числом 2. В появившемся окне отредактируем названия функций «плохая» и «хорошая».

Рис.9

Для входного блока «платежеспособность» это будет тип trapmf с общим числом 3. В появившемся окне отредактируем названия функций «плохая», «средняя» и «хорошая».

Рис.10

Для выходного блока «ставкакредита» это будет тип trimf с общим числом 3. В появившемся окне отредактируем названия функций «высокий», «средний» и «низкий». В поле Range установим диапазон [0 30], пусть процент по кредиту не превышает 30%.

Рис.11

Теперь создадим правила. Вспомним их:

• Если кредитная история хорошая, платежеспособность хорошая, то % ставка по кредиту низкий.
• Если кредитная история хорошая, платежеспособность средняя, то % ставка по кредиту средняя.
• Если кредитная история плохая, платежеспособность плохая, то % ставка по кредиту высокая.

Для этого выберем пункт меню Edit→Rules… в открывшемся окне Rule Editor: Newzadaca выбираем: значение первого входного блока «кредитистория» - хорошая, значение второго входного блока «платежеспособность» - хорошая, значение выходного блока «%кредита» - низкий, указываем Connection → And, нажимаем кнопку Add rule, аналогично для второго и третьего правил.

Рис.12

Сохраняем нашу систему File→Export→To File → →C:\Users\Desktop\Newzadaca.fis.

Откроем через пункт меню View/View rules… окно просмотра правил и зададим значение переменных для «кредитистория» – 1(т.е. хорошая), для «платежеспособность» – 1(т.е. хорошая). Видим ответ «ставкакредита» – 4,9 (т.е. низкий).

Рис.13

Проверим другие варианты. Зададим значение переменных для «кредитистория» – 0 (т.е. плохая), для «платежеспособность» – 0 (т.е. плохая). Видим ответ «ставкакредита» – 25,1 (т.е. высокий).