ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 65
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ
(ТУСУР)
Кафедра компьютерных систем в управлении и проектировании
(КСУП)
Отчёт по контрольной работе № 2
по дисциплине
«Вычислительная математика»
Томск – 2021
Оглавление
1.Решение уравнений с одной переменной 3
1.1.Задание 3
1.2.Теоретический материал (метод золотого сечения) 4
1.3.Алгоритм решения 4
1.4.Результаты работы программы 5
Выводы 6
Список использованных источников 7
Приложение А. Листинг программы 8
-
Решение уравнений с одной переменной
-
Задание
Написать программу отделения корней и их уточнения одним из нижеперечисленных методов:
-
методом дихотомии; -
методом хорд; -
методом золотого сечения; -
методом Ньютона; -
методом итераций; -
комбинированным методом
Входные данные:
-
функция f(x) и её первая и вторая производные (для метода Ньютона, итераций и комбинированного метода); -
интервал [a, b]; -
точность по аргументу и по функции ε1, ε2.
Выходные данные:
-
корни ξi, точность; -
значения f(ξi); -
количество итераций n; -
количество вычислений функции f(x); -
время счета; -
параметр сходимости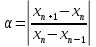 , где n – порядок сходимости.
, где n – порядок сходимости.
Вариант 7:
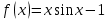
-
Теоретический материал (метод золотого сечения)
Метод золотого сечения относится к интервальным методам (или методам исключения интервалов).
Точки деления интервала выбираются таким образом, чтобы выполнялось соотношение между интервалами:
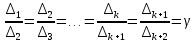
где
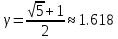 – золотое сечение, Δk = bk – ak – длина отрезка.
– золотое сечение, Δk = bk – ak – длина отрезка.-
Алгоритм решения
Представим алгоритм поиска нулей в форме последовательного выполнения итераций.
Задаём точки a1 = a, b1 = b, номер итерации k = 1.
Шаг 1. Определяем координаты золотого сечения:
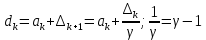
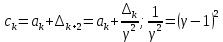
Вычисляем точку
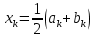
Шаг 2. Вычисляем значения функции f(ak), f(ck), f(dk), f(bk) и проверяем условия:
а) если f(ak) ·f(dk) ≤ 0, то ak+1 = ak; bk+1 =dk;
б) иначе если f(ck) ·f(bk) ≤ 0, то ak+1 = ck; bk+1 =bk;
Вычисляем новое приближение корня
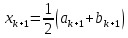 . Если
. Если 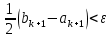 , то конец, иначе k = k + 1 и переход на шаг 1.
, то конец, иначе k = k + 1 и переход на шаг 1.Скорость сходимости линейная с коэффициентом α = γ – 1.
-
Результаты работы программы
| Входные данные | Выходные данные |
| a = 0 | Корень уравнения = 1.11383 |
| b = 2 | Точность по аргументу: 0.000733137 |
| eps = 0.001 | Точность по функции: 0.000733137 |
| | Количество итераций: 15 |
| | Количество вычислений функции f(x): 45 |
| | Время счёта (мс): 0.00758757 |
| | Параметр сходимости: 0.618034 |
| Входные данные | Выходные данные |
| a = 2 | Корень уравнения = 2.77262 |
| b = 6 | Точность по аргументу: 8.17127e-005 |
| eps = 0.0001 | Точность по функции: 2.67915e-005 |
| | Количество итераций: 21 |
| | Количество вычислений функции f(x): 63 |
| | Время счёта (мс): 0.00937288 |
| | Параметр сходимости: 0.618034 |
| Входные данные | Выходные данные |
| a = 4 | Корень уравнения = 6.43912 |
| b = 8 | Точность по аргументу: 4.10606e-007 |
| eps = 0.00001 | Точность по функции: 4.81611e-007 |
| | Количество итераций: 32 |
| | Количество вычислений функции f(x): 96 |
| | Время счёта (мс): 0.0107119 |
| | Параметр сходимости: 0.618034 |
| Входные данные | Выходные данные |
| a = 8 | Корень уравнения = 9.31724 |
| b = 12 | Точность по аргументу: 2.71445e-011 |
| eps = 1e-10 | Точность по функции: 8.23648e-011 |
| | Количество итераций: 52 |
| | Количество вычислений функции f(x): 156 |
| | Время счёта (мс): 0.0160678 |
| | Параметр сходимости: 0.618034 |
Выводы
В ходе выполнения данной контрольной работы были изучены методы решения уравнений одной переменной, написана реализация алгоритма решения задачи методом золотого сечения на языке программирования C++.
Список использованных источников
-
Бахвалов, Н. С. Численные методы : учеб. Пособие для вузов / Н. С. Бахвалов, Н.П. Жидков, Г. М. Кобельков. – М. : БИНОМ. Лаборатория знаний, 2011. – 637 с. -
Мицель, А. А. Вычислительные методы : учеб. Пособие / А. А. Мицель. – Томск : В-Спектр, 2010. – 264 с. -
Мицель, А. А. Практикум по численным методам / А. А. Мицель. – Томск : ТУСУР, 2004. – 196 с. -
Романенко, В. В. Вычислительная математика. Лабораторные работы / В. В. Романенко. – Томск : ТУСУР, 2006. – 114 с. -
Самарский, А. А. Задачи и упражнения по численным методам / А. А. Самарский, П. Н. Вабишевич, Е. А. Самарская. – М. : Эдиториал УРСС, 2009. – 208 с. -
Образовательный стандарт вуза ОС ТУСУР 01–2013. Работы студенческие по направлениям подготовки и специальностям технического профиля. Общие требования и правила оформления [Электронный ресурс] / А. А. Чернышев. – Томск : ТУСУР, 2013. – 57 с. – Режим доступа: https://regulations.tusur.ru/documents/70 (дата обращения: 20.04.2021).
Приложение А. Листинг программы
#include
#include
#include
#include
using namespace std;
// функция f(x), вариант 7
int fc = 0;
double f(double x)
{
fc ++;
return x * sin(x) - 1;
}
// вычисление корня уравнения методом золотого сечения
void GoldenSection(double a0, double b0, double eps1, double eps2)
{
// значение отношения золотого сечения
const double gama = (sqrt(5) + 1) / 2;
double a = a0, b = b0, c, d, delta;
double x = (a + b) / 2;
bool f1, f2;
int k = 0;
// засекаем время начала вычислений
__int64 freq, start, stop;
QueryPerformanceFrequency((LARGE_INTEGER *)&freq);
QueryPerformanceCounter((LARGE_INTEGER *)&start);
// алгоритм нахождения корня
do {
// шаг 1
delta = b - a;
d = a + delta / gama;
c = a + delta / pow(gama, 2);
// шаг 2
if (f(a) * f(d) <= 0)
b = d;
else
a = c;
x = (a + b) / 2;
// проверяем условия достижения точности
f1 = ((b - a) / 2 < eps1); // по аргументу
f2 = (fabs(f(x)) < eps2); // по значению функции
k ++;
} while (!(f1 && f2));
// засекаем вреия завершения вычислений
QueryPerformanceCounter((LARGE_INTEGER *)&stop);
double t = ((double)(stop - start) / freq) * 1000;
// вывод результатов
cout << "Корень уравнения: " << x << endl;
cout << "Точность по аргументу: " << (b - a) / 2 << endl;
cout << "Точность по функции: " << fabs(f(x)) << endl;
cout << "Количество итераций: " << k << endl;
cout << "Количество вычислений функции f(x): " << fc - 1 << endl;
cout << "Время счёта (мс): " << t << endl;
cout << "Параметр сходимости: " << gama - 1 << endl;
}
int main(int argc, char** argv)
{
setlocale(LC_ALL, "Russian");
double a, b, eps;
cout << "a = "; cin >> a;
cout << "b = "; cin >> b;
cout << "eps = "; cin >> eps;
GoldenSection(a, b, eps, eps);
return 0;
}