Файл: Моделирование и использование моделей в медицине. Этапы математического моделирования.docx

На настоящий момент времени сформировалось представление о том, что может дать применение метода математического моделирования в медицине: систематизировать важные параметры (физиологически содержательные свойства) и определять общую чувствительность системы вариации каждого параметра, количественно оценивать трудно измеряемые и вообще не измеряемые показатели, быстро и эффективно проверять гипотезы без обращения к эксперименту, планировать эксперименты и исследования, предсказывать поведение реальной системы.

Успех математического моделирования в медицине зависит от того, насколько глубоко исследованы системы организма и на этой основе эффективно выделены информативные подпространства признаков. Авторы моделей в математическом описании функций организма отражают физические, биохимические, физиологические и структурные характеристики объекта исследования.

Важной проблемой математического моделирования в медицине является адекватность математического выражения биологического явления. Проблемность этой ситуации состоит в том, что математический аппарат создавался в расчете на изучение процессов неживой природы (механических, атомных, молекулярных), характеризующихся одномерным распределением, которое не свойственно биопроцессам.

Построение математических моделей биосистем подразумевает проведение экспериментальных исследований для получения количественных характеристик изучаемых процессов. В дальнейшем эти характеристики становятся объектом исследования и на их основе с учетом теоретических предпосылок строится модель, объясняющая функционирование изучаемого объекта. Наивысшей точкой такого обобщения является математическая модель, заменяющая реальный объект исследования. Построенная модель представляет собой некоторое упрощение реального объекта как по структуре, так и по сложности внешних и внутренних связей, но обязательно отражает те свойства объекта, которые являются целью исследования. В дальнейшем модель подвергается всесторонней проверке и корректировке для более полного соответствия модели и реального объекта. Рассмотрим более подробно основные этапы моделирования:

1.Постановка задачи, которая заключается в определении цели исследования и моделирования на основании некоторой первоначальной гипотезы.

2.Построение функциональной системы объекта - определение входов и выходов, режимов изменения входных воздействий, исследуемых режимов (норма, патология).

---

3.Планирование эксперимента. На этом этапе определяют режимы изменения входных сигналов, внутренних состояний системы, производится обработка комплекса контрольно - измерительной аппаратуры.

4.Проведение серии пробных опытов для обработки методики исследований, приемлемости принятых допущений, проверки исходной гипотезы.

5.Проведение основной серии опытов для получения статических и динамических характеристик.

6.Предварительная статистическая обработка материала, полученного на стадии экспериментирования с биосистемой.

7.Выбор типа и вида модели на основании анализа результатов статистической обработки данных.

8.Определение параметров модели по результатам экспериментов. 9.Всестороннее исследование математической модели биосистемы с

целью определения достоверности и границ применимости модели. Сравнение результатов, полученных с помощью модели и реального объекта, позволяет определить основные показатели качества модели:

• 
  информативность, оценивается корреляцией между экспериментальным значением отклика системы на внешние воздействия и значением отклика, рассчитанным по модели;
  
• 
  адекватность, означает отражение моделью с заданной точностью определенной совокупности свойств объекта;
  

• устойчивость коэффициентов регрессии и структуры модели. Направленность на клиническое применение определила особые

требования к математическим моделям: необходимость отражения математических процессов и компенсаторных сдвигов, лечебных воздействий (медикаментозных, измерение режима вентиляции, жидкостного баланса и пр.), представление клинического контроля, оценку модели в реальном времени, а также наличие интерактивного интерфейса в терминах, принятых в клинике.

В настоящее время возрос интерес к использованию методов математического моделирования при создании новых лекарственных средств. Хранение и обработка информации о структуре и биологическом действии химических соединений, поиск оригинальных базовых структур во внутрифирменных и коммерчески доступных банках данных, установление связи структура - свойство и оптимизация свойств активных субстанций, анализ структурных особенностей новых биологических мишеней действия лекарств, моделирование взаимодействия лиганд - рецептор, минимизация функционально активных фрагментов эндогенных биорегуляторов, комбинаторная химия - вот лишь некоторые из проблем, эффективное решение которых было бы невозможно без современных компьютерных технологий.

---

В июне 1996 года на базе Института биомедицинский химии РАМН создано Российское отделение Международного общества по анализу количественных соотношений структура - активность и молекулярному моделированию, что позволило расширить возможности компьютерного прогнозирования. В результате работы коллектива в этом направлении была создана компьютерная система РА88, которая одновременно предсказывает вероятность более чем 100 фармакологических эффектов и механизмов действия вещества на основе его структурной формулы. Эффективность применения этого подхода к планированию скрининга составляет около 800%, а точность компьютерного прогноза на 300% превосходит предсказание экспертов.

Итак, одним из конструктивных инструментов получения новых знаний и решений в медицине является метод математического моделирования. Процесс математизации медицины - частое проявление взаимопроникновения научных знаний, повышающее эффективность лечебно - профилактической работы.

Математическая модель «хищники-жертвы»

Впервые в биологии математическую модель периодического изменения числа антагонистических видов животных предложил итальянский математик В. Вольтерра с сотрудниками. Модель, предложенная Вольтерра, явилась развитием идеи, намеченной в 1924 году А. Лоттки в книге «Элементы физической биологии». Поэтому эта классическая математическая модель известна как модель «Лоттки-Вольтерра».

Хотя в природе отношения антагонистических видов более сложные, чем в модели, тем не менее они являются хорошей учебной моделью, на которой можно изучать основные идеи математического моделирования.

Итак, задача: в некотором экологически замкнутом районе живут два вида животных (например, рыси и зайцы). Зайцы (жертвы) питаются растительной пищей, имеющейся всегда в достаточном количестве (в рамках данной модели не учитывается ограниченность ресурсов растительной пищи). Рыси (хищники) могут питаться только зайцами. Необходимо определить, как будет меняться численность жертв и хищников с течением времени в такой экологической системе. Если популяция жертв увеличивается, вероятность встреч хищников с жертвами возрастает, и, соответственно, после некоторой временной задержки, растет популяция хищников. Эта достаточно простая модель вполне адекватно описывает взаимодействие между реальными популяциями хищников и жертв в природе.

---

Теперь приступим к составлению дифференциальных уравнений. Обозначим число жертв через N, а число хищников через M. Числа N и M являются функциями времени t. В нашей модели учтем следующие факторы:

а) естественное размножение жертв;

б) естественная гибель жертв;

в) уничтожение жертв за счет поедания их хищниками;

г) естественное вымирание хищников;

д) увеличение числа хищников за счет размножения при наличии пищи.

Так как речь идет о математической модели, то задачей является получение уравнений, в которые входили бы все намеченные факторы и которые описывали бы динамику, то есть изменение числа хищников и жертв со временем.

Пусть за некоторое время t количество жертв и хищников изменится на ∆Nи ∆M. Изменение числа жертв ∆N за время ∆t определяется, во-первых, увеличением в результате естественного размножения (которое пропорционально имеющемуся количеству жертв):

N₁ = A∙N∙∆t, (1)

где А – коэффициент пропорциональности, характеризующий скорость размножения жертв в данных условиях.

Во-вторых, имеет место уменьшение числа жертв из-за естественного вымирания, тоже пропорциональное их числу в данный момент:

N₂ = - B∙N∙∆t, (2)

где В – коэффициент пропорциональности, характеризующий скорость естественного вымирания жертв.

В основе вывода уравнения, описывающего уменьшение числа жертв из-за поедания их хищниками, лежит идея о том, что чем чаще происходит их встреча, тем быстрее уменьшается число жертв. Ясно также, что частота встреч хищников с жертвой пропорционально и числу жертв и числу хищников, то есть их произведению. Поэтому можно записать:

N₃ = - C∙N∙M∙∆t, (3)

где С – коэффициент пропорциональности, характеризующий частоту встреч жертвы с хищником.

В итоге, с учетом всех трех факторов для изменения числа жертв, можно записать следующее уравнение:

N = A∙N∙∆t - B∙N∙∆t - C∙M∙N∙∆t (4)

Поделив левую и правую часть уравнения (4) на ∆t и перейдя к пределу при ∆t→0, получим дифференциальное уравнение первого порядка:

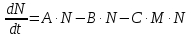(5)

Для того, чтобы решить это уравнение, нужно знать, как меняется число хищников (

---

М) со временем. Изменение числа хищников (∆М) определяется увеличением из-за естественного размножения при наличии достаточного количества пищи (М₁ = Q∙N∙M∙∆t) и уменьшением из-за естественного вымирания хищников (M₂ = - P∙M∙∆t):

M = Q∙N∙M∙∆t - P∙M∙∆t(6)

Из уравнения (6) можно получить дифференциальное уравнение:

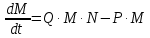(7)



Дифференциальные уравнения (5) и (7) представляют собой математическую модель «хищники-жертвы». Достаточно определить значения коэффициентов A, B, C, Q, P и математическую модель можно использовать для решения поставленной задачи.

Проверка и корректировка математической модели. В данной лабораторной работе предлагается кроме просчета наиболее полной математической модели (уравнения 5 и 7), исследовать более простые, в которых что-либо не учитывается.

Рассмотрев пять уровней сложности математической модели, можно «почувствовать» этап проверки и корректировки модели.

• 
  1-ый уровень – в модели учтено для «жертв» только их естественное
  

размножение, «хищники» отсутствуют;

• 
  2-ой уровень – в модели учтено для «жертв» их естественное
  

вымирание, «хищники» отсутствуют;

• 
  3-ий уровень – в модели учтены для «жертв» их естественное
  

размножение и вымирание, «хищники» отсутствуют;

• 
  4-ый уровень – в модели учтены для «жертв» их естественное
  

размножение и вымирание, а также поедание

«хищниками», но число «хищников» остается

неизменным;

• 
  5-ый уровень – в модели учтены все обсуждаемые факторы.
  

Итак, имеем следующую систему дифференциальных уравнений:


,

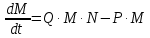где М – число «хищников»;

N – число «жертв»;

t – текущее время;

A – скорость размножения «жертв»;

C – частота встреч «хищники»-«жертвы»;

B – скорость вымирания «жертв»;

Q – размножение «хищников»;

P – вымирание «хищников».
1-ый уровень: М = 0, В = 0;

2-ой уровень: М = 0, А = 0;

---