Файл: Задача в таблице приведено распределение 120 коров по дневному надою (в кг) и по жирности (в %).docx

Задача 6. В таблице приведено распределение 120 коров по дневному надою 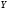(в кг) и по жирности 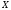(в %):

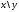	7	9	11	13	15	Итого
3,3				8		8
3,5			2	16	8	26
3,7		4	16	10	2	32
3,9	2	6	10	2		20
4,1	8	6	20			34
Итого	10	16	48	36	10	120

Необходимо:

1) Вычислить групповые средние 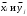и построить эмпирические линии регрессии;

2) Предполагая, что между переменными X и Y существует линейная корреляционная зависимость:

а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений;

---

б) вычислить коэффициент корреляции, на уровне значимости α = 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными X и Y;

в) используя соответствующее уравнение регрессии, оценить средний процент жирности молока для коров, дневной удой которых составляет 12 кг.

Решение.

1) Найдем групповые средние по формулам: ; .

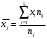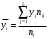Вычисления проведем в Excel, получаем:

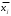	4,060	3,925	3,900	3,533	3,540
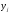	7	9	11	13	15

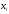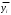3,3	13,000
3,5	13,462
3,7	11,625
3,9	10,200
4,1	9,706

Построим эмпирические линии регрессии ( на , на ).



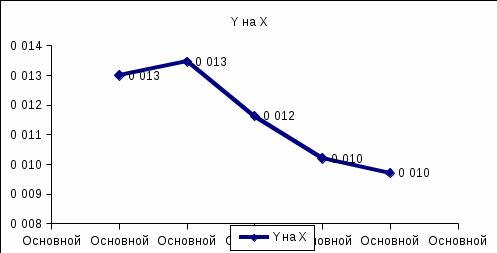
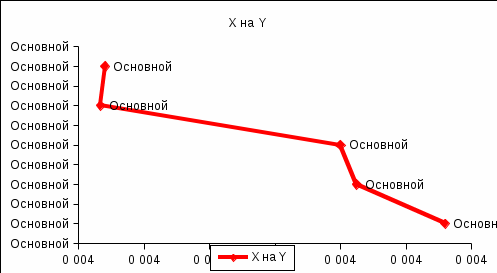
Из вида эмпирических линий регрессии можно заключить, что между переменными наблюдается линейная зависимость.

---

Найдем уравнения прямых линий регрессии. Вычислим необходимые величины (расчеты в таблицах ниже):

	3,3	3,5	3,7	3,9	4,1	Сумма
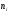	8	26	32	20	34	120
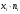	26,4	91	118,4	78	139,4	453,2
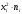	87,12	318,5	438,08	304,2	571,54	1719,44

	7	9	11	13	15	Сумма
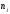	10	16	48	36	10	120
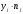	70	144	528	468	150	1360
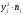	490	1296	5808	6084	2250	15928

---

, ,

,


, ,

,

.

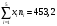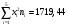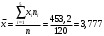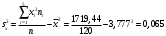
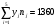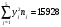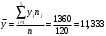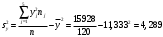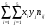= 5093,2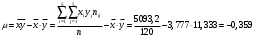








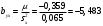
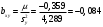
Уравнения прямых регрессии:




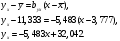
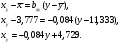
Построим графики линий регрессии на одном чертеже с эмпирическими линиями регрессии.





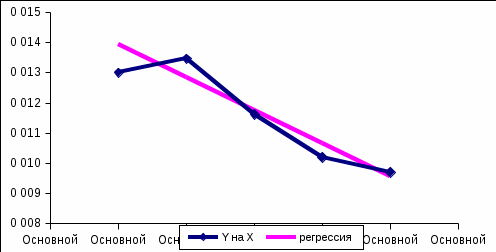
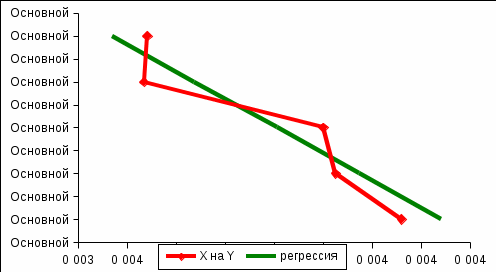
Экономическая интерпретация полученных уравнений:

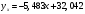- при увеличении жирности молока на 1%, дневной надой уменьшается в среднем на 5,483 кг.

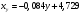- при увеличении дневного надоя на 1 кг, жирность молока уменьшается в среднем на 0,084 %.
Вычислим коэффициент корреляции
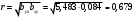
На уровне значимости 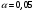оценим значимость коэффициента корреляции. Вычислим значение критерия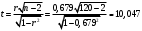

По таблице критерия Стьюдента для уровня значимости 0,05 находим 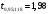. Так как наблюдаемое значение 10,047 больше критического, коэффициент корреляции значим.
Связь между переменными X и У тесная, обратная.
Используя соответствующее уравнение регрессии, оценим средний процент жирности молока для коров, дневной удой которых составляет 12 кг:

.

---
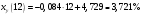