Файл: Вычисления Задание 1.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 05.12.2023

Просмотров: 654

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Вычисления Задание 1. Килограмм орехов стоит 75 рублей. Маша купила 4 кг 400 г орехов. Сколько рублей сдачи она должна получить с 350 рублей?▼ Найдем стоимость покупки: 4 кг 400 г орехов стоит 4,4·75 = 330 рублей. Значит, с 350 рублей Маша получит сдачи 350 − 330 = 20 рублей.Ответ: 20.▲ Задание 2. Поезд Казань-Москва отправляется в 21:35, а прибывает в 10:35 на следующий день (время московское). Сколько часов поезд находится в пути?▼ В день отправления поезд едет (24 − 21)·60 − 35 = 3·60 − 35 = 145 минут, а на следующий день до момента прибытия он едет 10·60 + 35 = 635 минут. Всего в пути поезд проведет 145 + 635 = 780 минут. Разделим 780 на 60: 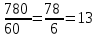. Значит, поезд находится в пути 13 часов. Ответ: 13.▲ Задание 3. На счету Машиного мобильного телефона было 53 рубля, а после разговора с Леной осталось 8 рублей. Сколько минут длился разговор с Леной, если одна минута разговора стоит 2 рубля 50 копеек?▼ Разговор с Леной стоил Маше 53 − 8 = 45 рублей. Разделим 45 на 2,5: 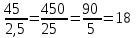 . Значит, разговор с Леной длился 18 минут. Ответ: 18.▲Округление — математическая операция, позволяющая уменьшить количество знаков в записи числа за счет замены числа его приближенным значением. Округление производится постепенно справа налево в соответствии со следующими правилами: • если первая из отбрасываемых цифр меньше 5, то последняя сохраняемая цифра не изменяется; • если первая из отбрасываемых цифр равна 5 или больше 5, то последняя сохраняемая цифра увеличивается на единицу. Округление следует выполнять сразу до желаемого количества значащих цифр, а не по этапам. Например, округляя число 3,14159265 до трех, четырех и восьми знаков, получим соответственно: 3,14, 3,142, 3,1415927. Среди заданий наиболее часто встречаются задания двух видов:• Округ­ле­ние с недостатком. Сколько карандашей по цене 2 руб. можно купить на 5 рублей? Ответ: 2 карандаша - округляем до ближайшего меньшего целого, т. к. половину карандаша купить невозможно; • Округ­ле­ние с избытком. Сколько двухлитровых банок потребуется, чтобы в них поместилось 5 литров воды? Ответ: 3 банки - округляем до ближайшего большего целого

, т. к. вся вода должна поместиться.

Округ­ле­ние с недостатком

Задание 1. На одну порцию рисовой каши требуется 40 грамм риса и 0,12 литра молока. Какое наибольшее количество порций каши может приготовить столовая, если в ее распоряжении есть 900 грамм риса и 3 литра молока?

▼ Из девятисот грамм риса можно приготовить 900:40 = 22,5 порций каши.

Из трех литров молока можно приготовить 3:0,12 = 25 порций каши.

  Следовательно, продуктов достаточно только на 22 порции каши.

 Ответ: 22.▲

Задание 2. Сырок стоит 7 рублей 20 копеек. Какое наибольшее число сырков можно купить на 60 рублей?

▼ Разделим 60 на 7,2:

.

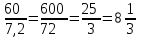Значит, на 60 рублей можно купить 8 сырков.

 Ответ: 8. ▲

Задание 3. Шоколадка стоит 35 рублей. В воскресенье в супермаркете действует специальное предложение: заплатив за две шоколадки, покупатель получает три (одну в подарок). Какое наибольшее количество шоколадок можно получить, потратив не более 200 рублей в воскресенье?

▼ Разделим 200 на 35:

.

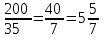Значит, можно будет купить 5 шоколадок. Еще 2 будут даны в подарок. Всего можно будет получить 7 шоколадок.

 Ответ: 7.▲

Задание 4. На день рождения полагается дарить букет из нечетного числа цветов. Тюльпаны стоят 30 рублей за штуку. У Вани есть 500 рублей. Из какого наибольшего числа тюльпанов он может купить букет Маше на день рождения?

▼ Разделим 500 на 30:

.

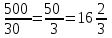Ване хватает денег на 16 тюльпанов, но цветов должно быть нечетное число. Следовательно, Ваня может купить букет из 15 тюльпанов.

 Ответ: 15.▲

Округление с избытком

Задание 1. Больному прописано лекарство, которое нужно пить по 0,5 г 3 раза в день в течение 21 дня. В одной упаковке 10 таблеток лекарства по 0,5 г. Какого наименьшего количества упаковок хватит на весь курс лечения?

▼ Больному нужно выпить 0,5·3·21 = 31,5 г лекарства. В одной упаковке содержится 0,5·10 = 5 г лекарства. Разделим 31,5 на 5:

.

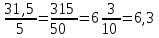Значит, на курс лечения шести упаковок не хватит, требуется 7 упаковок.

 Ответ: 7.▲

Задание 2. В летнем лагере на каждого участника полагается 40 г сахара в день. В лагере 181 человек. Сколько килограммовых упаковок сахара понадобится на весь лагерь на 5 дней?

▼ На 181 человека на 1 день полагается 181·40 = 7240 г сахара, на 5 дней - 7240·5 = 36 200 г. Разделим 36 200 г на 1000 г в одной упаковке:36 200: 1000 = 36,2.Тем самым, на весь лагерь на 5 дней 36 упаковок не хватит, следовательно, понадобится 37 килограммовых упаковки сахара. Ответ: 37.▲ Задание 3. Для ремонта квартиры требуется 63 рулона обоев. Сколько пачек обойного клея нужно купить, если одна пачка клея рассчитана на 6 рулонов?▼ Разделим 63 на 6, получим 10,5. Следовательно, понадобится 11 пачек клея. Ответ: 11.▲ Задание 4. В доме, в котором живёт Женя, один подъезд. На каждом этаже по восемь квартир. Женя живёт в квартире 87. На каком этаже живёт Женя?▼ Разделим 87 на 8: 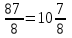.Значит, Женя живет на 11 этаже. Ответ: 11.▲Задание 5. Для приготовления маринада для огурцов на 1 литр воды требуется 12 г лимонной кислоты. Лимонная кислота продается в пакетиках по 10 г. Какое наименьшее число пачек нужно купить хозяйке для приготовления 6 литров маринада?▼ Для приготовления 6 литров маринада потребуется 12·6 = 72 г лимонной кислоты. Разделим 72 на 10: 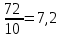. Значит, нужно будет купить 8 пакетиков. Ответ: 8.▲Отношение и пропорцииОтношением двух чиселa, b называется частное этих чисел a и b, т.е. 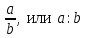. 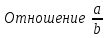показывает, во сколько раз первое число больше второго. 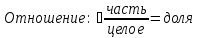. Например, 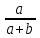- доля числа a; 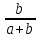- доля числа b. Пример. В классе 12 девочек и 24 мальчика.▼ Отношение 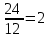показывает, что мальчиков в 2 раза больше, чем девочек, или на 1 девочку приходится 2 мальчика.
Отношение 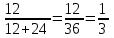- доля девочек в классе, отношение 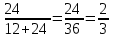- доля мальчиков в классе, причем доля девочек (1/3) + доля мальчиков (2/3) = 1.▲ Пример. Заменить отношение дробных чисел 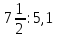отношением целых чисел.▼ 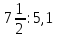= = 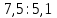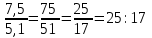▲ Пример. Из 42 поездов, приходящих на станцию, отношение пассажирских к скорым поездам составляет 4:3. Сколько скорых поездов приходит на станцию?▼ 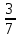- доля скорых поездов, тогда число скорых поездов есть 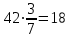▲Пример. Два карандаша и три ластика были куплены за 45 руб., а три карандаша и четыре ластика – за 65 руб. Сколько стоит один карандаш и один ластик?▼ Пусть x, y – стоимость одного карандаша и одного ластика, соответствен-но. По условиям примера составляем уравнения: 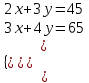; 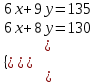x = 15, y = 5.Тогда один карандаш и один ластик стоят x + y = 15 + 5 = 20 руб. ▲ПропорцииПропорцией называется равенство двух отношений, т.е. 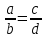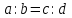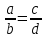, или .Основное свойство пропорции: 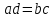 .Используя основное свойство пропорции, можно найти ее неизвестный член, если все ее остальные члены известны. Например:

  1. ;

  2. , .
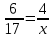
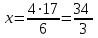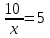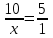
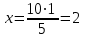Прямо и обратно пропорциональные величины Две величины a, b называются прямо пропорциональными, если при увеличении одной из них в несколько раз другая также увеличивается во столько же раз. Если две величины a, b прямо пропорциональны, то отношение соответствующих значений этих величин равны, т.е. a1/a2 = b1/b2. Пример 1. Автобус проехал 100 км, при этом расход топлива составил 27 л. Сколько литров топлива потребуется, чтобы проехать 200 км ?▼ Составим схему по условию задачи:

100 км ------ 27 л

200 км ------ х
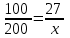
Зависимость между расходом топлива и расстоянием прямо пропорциональная, так как если проехать в несколько раз больше, то и расход топлива увеличится во столько же раз. Условно обозначим такую зависимость одинаково направленными стрелками.Запишем пропорцию: 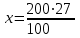 = 54 л.Ответ. 54 л.▲ Две величины a, b называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая, наоборот, уменьшается во столько же раз. Если две величины a, b обратно пропорциональны, то отношение значений одной из них равно обратному отношению соответствующих значений другой величины, т.е. a1/a2

Смотрите также файлы