Файл: Реферат Разработка методики ультразвукового контроля бурильных труб.doc
Добавлен: 11.12.2023
Просмотров: 214
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1. Эксплуатация бурильных труб
1.1. Сборка и комплектование бурильных труб
2.6. Гидроиспытание бурильных труб
3. Дефектоскопия бурильных труб
3.1. Ультразвуковой импульсный толщиномер типа «Кварц»
3.2. Передвижная комплексная дефектоскопическая установка типа ПКДУ-1
4. Измерение скоростей распространения волн Похгаммера
5.1. Описание экспериментальной установки
5.3. Определение амплитуды донного импульса
5.4. Определение амплитуды дефекта и шума
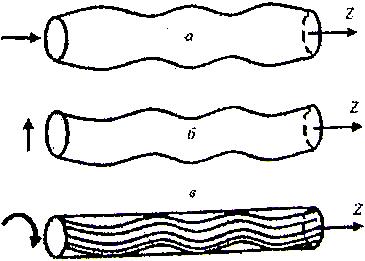
Рисунок 2. Нормальные волны в стержнях:
а - симметричные; б - антисимметричные; в – крутильные
Рисунок 3. Дисперсионные кривые фазовых скоростей волн Похгаммера в стержне (v=0.29).
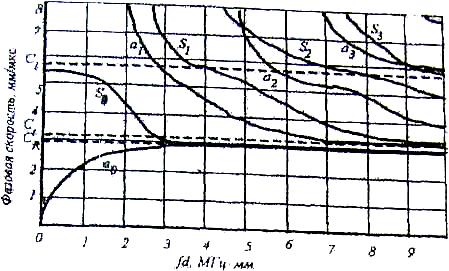
На рисунке 3 показана система дисперсионных кривых фазовых скоростей волн Похгаммера для стержня с коэффициентом Пуассона v=0.29. Как видно из кривых, для всех номеров волн характерно наличие дисперсии скорости, т.е. их скорость довольно сложно зависит от диаметра стержня и частоты. Нулевая симметричная So и антисимметричная ао моды качественно отличаются от всех остальных волн тем, что существуют при любых частотах и диаметрах. При fd<4 МГц-мм (f- частота, d- диаметр стержня), их фазовые и групповые скорости стремятся к скорости рэлеевской волны CR.
При fd<2 МГц-мм существуют только моды нулевых порядков, волны первого и более высоких порядков возникают при определенных критических значениях для каждой моды. Эти значения соответствуют резонансам колебаний по толщине на продольных и поперечных волнах.
В области минимальной дисперсии скорости fd«l МГц-мм (при низкой частоте и малом диаметре стержня) фазовая и групповая скорости продольной волны нулевого порядка Cso стремятся к общему пределу -стержневой скорости волн Со и определяются выражением:
где Е - модуль Юнга, р - плотность среды, v - коэффициент Пуассона, С, - скорость поперечной волны в безграничной среде.
Фазовая скорость распространения изгибной волны а0, в интервале частот, удовлетворяющих условию fd
где f- частота волны.
Для крутильной волны нулевого порядка как фазовая, так и групповая скорости не зависят от частоты. Скорость крутильных волн Ст зависти от формы поперечного сечения, но для любой данной формы она постоянна:
где D - крутильная жесткость, I - момент инерции, р - плотность материала стержня. Для кругового сечения радиуса г: D=μπr4/2, I= πr4/2 (μ - модуль сдвига), а скорость нулевой крутильной волны равна скорости поперечной волны:
Cт=(μ/ρ)1/2=С (4)
Фазовая скорость является основной характеристикой волны Похгаммера и определяет скорость распространения фазы волны вдоль стержня. Она позволяет вычислить длину волны, рассчитать напряжения и смещения в волне Похгаммера, необходима при расчетах условий возбуждения волн.
Знание величин скоростей стержневой и крутильных волн позволяет вычислить значения динамических упругих модулей исследуемых материалов. Решая систему уравнений (1), (4), можно найти, что
- модуль сдвига определяется формулой:
- модуль упругости (модуль Юнга):
- коэффициент Пуассона:
Значения Е, μ, v могут быть вычислены при известной плотности среды р. Знание значений упругих модулей позволяет, например, оценивать напряженное состояние материала при внешних механических воздействиях. Использование волн Похгаммера в области существенной дисперсии скорости существования нескольких мод приводит к искажению и ослаблению сигналов от дефектов и к сложности интерпретации возникающих в многомодовом волноводе искаженных сигналов. Искажения обусловлены как изменением фазовых соотношений между сигналами, переносимыми разными типами волн с увеличением расстояния, так и изменением распределения колебаний по сечению. В связи с этим для контроля прутков и измерениях с применением волн Похгаммера целесообразно использование симметричной моды So в области минимальной дисперсии скорости (малых произведений fd), либо использование нулевой крутильной моды, дисперсия в которой отсутствует. [5]
5. Экспериментальная часть
5.1. Описание экспериментальной установки
Экспериментальная установка состоит из следующих частей:
• блок ГПУ (генератор предусилитель);
• блок УКП (усилитель - коммутатор - питание);
• ЭМАП (электромагнитно - акустический преобразователь);
• системный блок;
• монитор.
5.2. Определение скорости
Определение скорости происходит следующим образом. При запуске экспериментальной установки, т.е. когда ЭМАП излучает акустические сигналы, а затем регистрирует отраженные от другого торца сигналы, и
преобразует их в электрические, на экране монитора наблюдается следующая картина, представленная на рисунке 4.
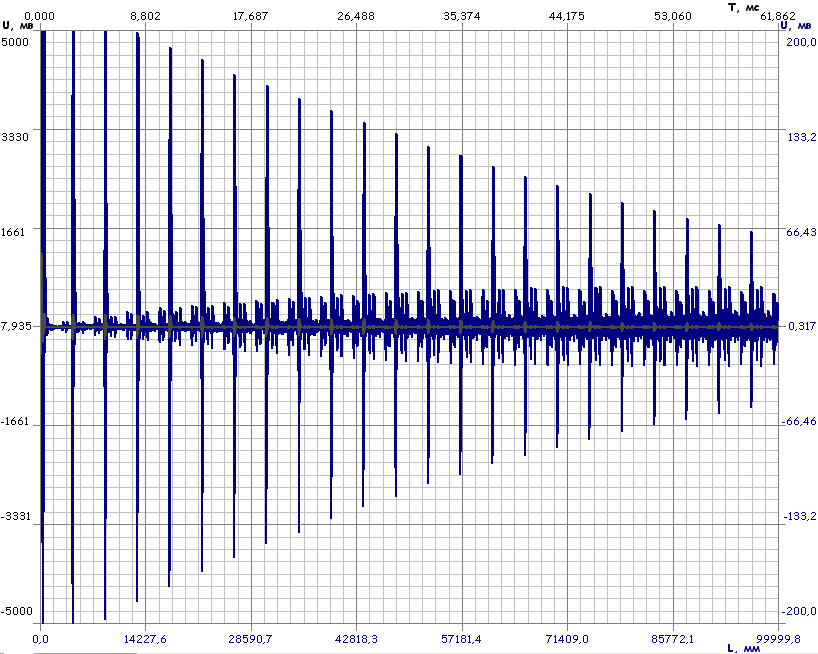
Рисунок 4. Общий вид
Так как время прохождения луча, прямо пропорционально пройденному пути, то на экране наблюдается диаграмма, по горизонтальной оси которой отложено время, пропорциональное расстоянию, пройденному волной в трубе, а по вертикальной оси отображается амплитуда импульсов.
Вычислим скорость V=s/t (8), где S-длина трубы
V=4394*2/2.718=3233м/с
5.3. Определение амплитуды донного импульса
На рисунке 5 изображена эхограмма первых и вторых донных импульсов, для контролируемой трубы. U=430мВ
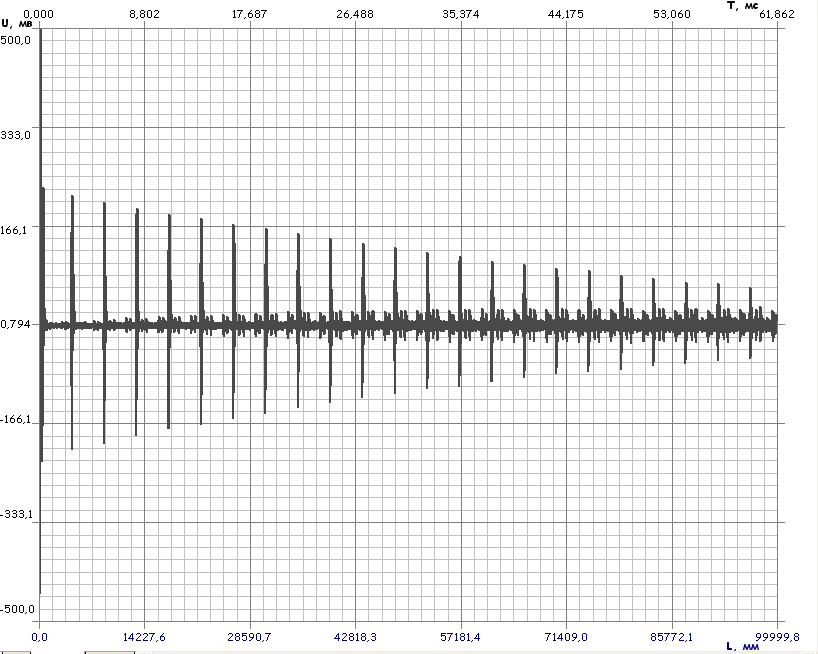
Рисунок 5. Эхограмма амплитуды донного импульса.
5.4. Определение амплитуды дефекта и шума
Создадим на трубе дефект в виде проточки. На экране наблюдаем следующую картину (рисунок 6). U=7,2 мВ, U=1.1 мВ.
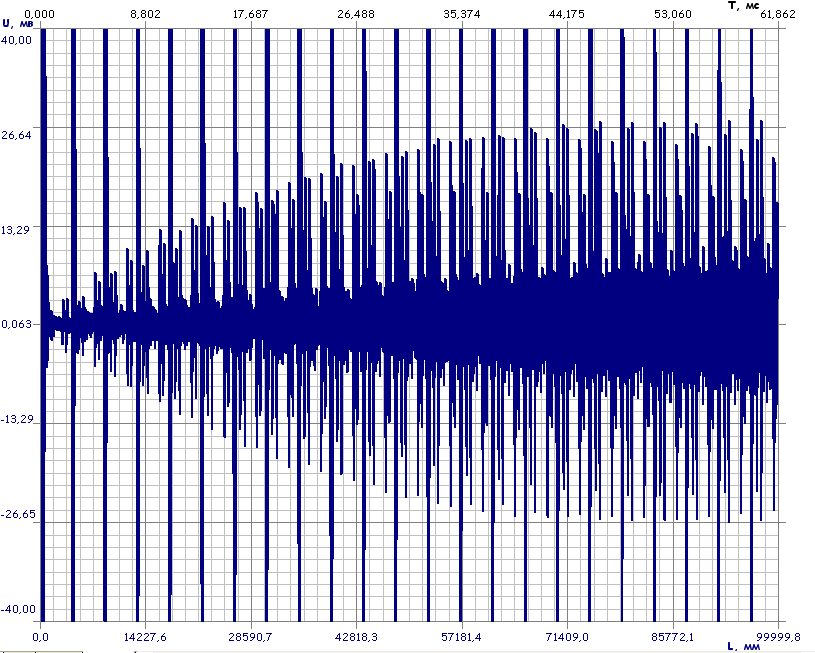
Рисунок 6. Эхограмма импульсов, создаваемых дефектами и шумы.
5.5. Определение затухания
Так как волна в стержне не расходится (можно считать ее плоской), то потери ультразвуковой энергии при ее распространении по стержню происходят только за счет внутреннего затухания. В условиях эксперимента уравнение крутильной волны может быть записано
Un{r)=U0e-δrn (9)
где Un (г) - амплитуда n-го отраженного импульса; Uo - амплитуда первого принятого импульса; δ - коэффициент затухания в объекте; rn - расстояние, пройденное крутильной волной за n отражений. rn =2nL.
После несложных преобразований можно получить следующую формулу для вычисления коэффициента затухания δ:
δ =ln(U0/U1)/ rn (10)
Таблица 3. – Затухание крутильной волны в трубе.
| № импульса | Амплитуда сигнала | Расстояние, пройденное волной*4394 | Коэффициент затухания *10-6 |
| 1 | 23 | | |
| 2 | 21,5 | 2 | 7,68 |
| 3 | 22,6 | 4 | 9,98 |
| 4 | 19,4 | 6 | 6,46 |
| 5 | 20,5 | 8 | 3,28 |
| 6 | 21,5 | 10 | 1,54 |
| 7 | 20,2 | 12 | 2,46 |
| 8 | 18,8 | 14 | 3,28 |
| 9 | 18,4 | 16 | 3,18 |
| 10 | 18,9 | 18 | 2,48 |
| 11 | 17,6 | 20 | 3,05 |
5.6. Определение отношений сигнал/шум и дефект/шум
Сигнал/шум = 430мВ/1,1мВ=390,9
Дефект/шум = 7,2МВ/1,1мВ=6,55
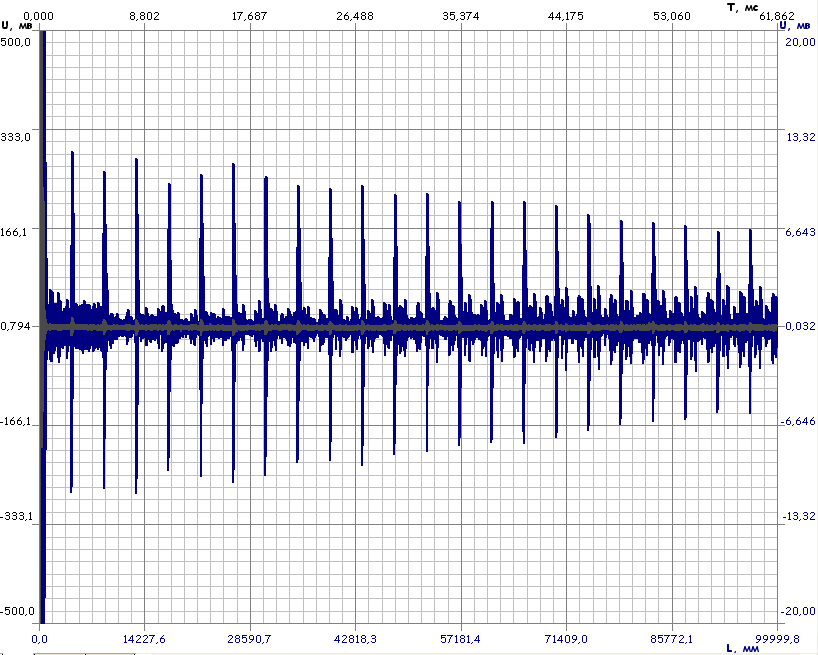
Рисунок 7. Затухание
6. Заключение
В ходе выполнения курсовой работы были проведены опыты на трубе НКТ-73 с помощью экспериментальной установки и были получены следующие результаты.
Скорость распространения крутильной волны в трубе составляет 3233 м/с.
Амплитуда донного импульса равна 430 мВ, амплитуда от дефекта 7,2 мВ. Рассчитаны отношения эхо от торцев и дефектов к амплитуде шума. Сигнал/шум=390,9, дефект/шум=6,55.
В ходе дальнейшего выполнения дипломной работы предполагается исследовать возможность применения крутильной волны для дефектоскопии бурильных труб. В частности:
-
Выбор рабочей частоты; -
Выбор основной закономерности распространения крутильных волн в бурильной трубе; -
Оценка уровня акустических шумов; -
Оценка «мертвой» зоны; -
Оценка чувствительности к дефектам.
Список литературы
-
Кадымов Я.Б. Вопросы автоматизации бурения нефтяных скважин. – М.:1967г. -
Руге Ю. Техника сварки. – М.: «Металлургия», 1984г. -
Султанов С.Г. Прогрессивная технология нефтепромыслового машиностроения. – М.:1969г. -
Ультразвуковые пьезопреобразователи для неразрушающего контроля. Под ред. Ермолова И.Н. – М.: «Машиностроение», 1986г. -
Приборы для неразрушающего контроля материалов и изделий. Под ред. Клюева В.В. – М.: «Машиностроение», 1976г. -
www.avto-lab.ru -
www.stpc.ru -
www.tmk-group.ru -
www.zond.spb.ru -
www.zbo.ru -
www.uvis.ua