Файл: Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых.docx

М инистерство науки и высшего образования Российской Федерации

Муромский институт (филиал)

федерального государственного бюджетного образовательного учреждения высшего образования

«Владимирский государственный университет

имени Александра Григорьевича и Николая Григорьевича Столетовых»
Факультет МСФ

Кафедра Техносферная безопасность
Практические работы

по Автоматизация систем ТГВ

( наименование дисциплины)


Руководитель

Середа С.Н.

(фамилия, инициалы)

_________________________

(подпись) (дата)
С тудент СТз-118

(группа)

Атрехалин А.А.

(фамилия, инициалы)



(подпись) (дата)


Муром 2023

Содержание




Практическая работа №1

Математические модели звеньев САР

Процессы, происходящие в автоматических системах, описываются в установившихся режимах при помощи алгебраических уравнений с постоянными коэффициентами, в неустановившихся режимах – дифференциальными и интегрально-дифференциальными уравнениями. Поскольку уравнения статики легко получить из уравнений динамики САР путем приравнивания в них нулю всех производных по времени переменных (координат состояния) и внешних воздействий, рассмотрим математическое описание САР в динамическом режиме.

---

Вариант 1





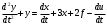
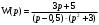
Задание 1.



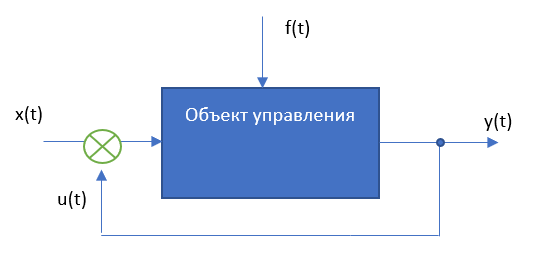
Рисунок 1 Схема объекта управления.

Выполним преобразование Лапласа к диф. уравнению и получим операторное уравнение:






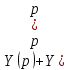
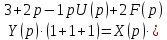
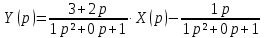
Передаточная функция ОУ:



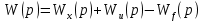
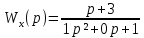– передаточная функция по каналу входного воздействия

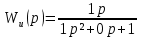- передаточная функция по каналу управления

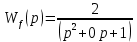- передаточная функция по каналу воздействия помехи

Структурная схема:



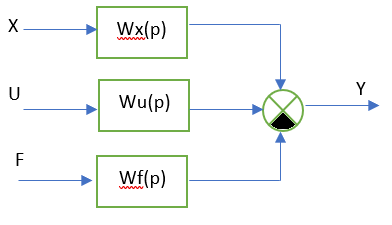
Далее в MATLAB пишем программу и строим графики.

Для вх. сигнала

Корни:

0.1 s

2s + 1

z = 0

p = - 0.5000



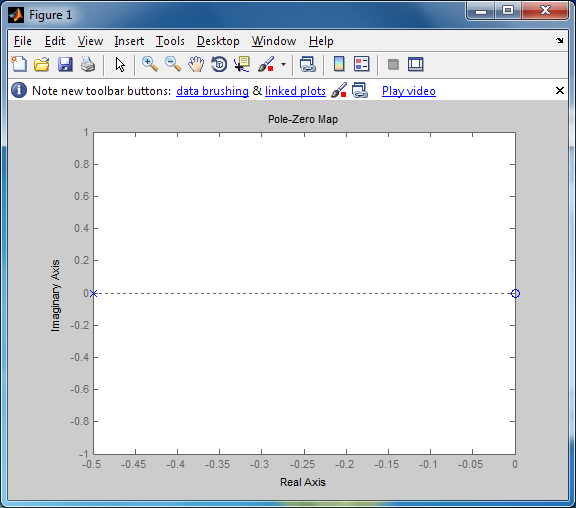
График расположения корней на комплексной плоскости





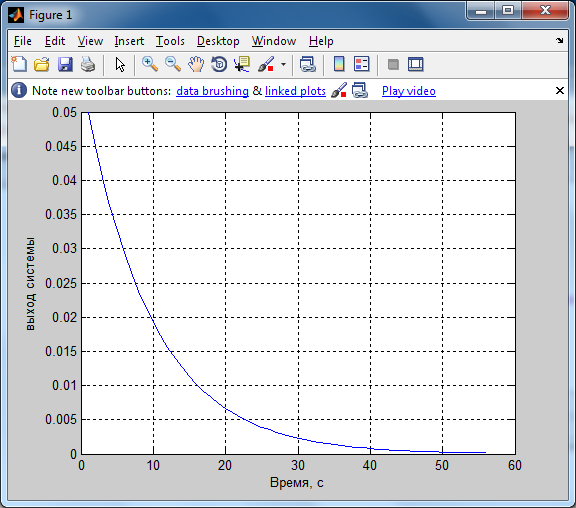
График переходной характеристики объекта (кривая разгона).



Задание 2.

Дана передаточная функция:



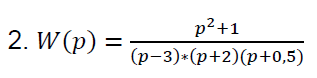
s - 10

s^2 + 3 s - 10





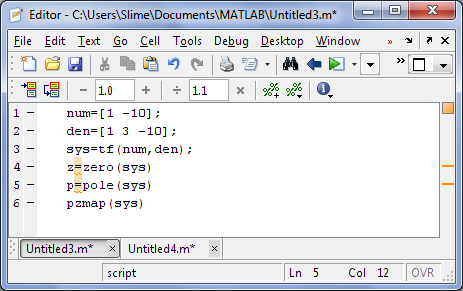
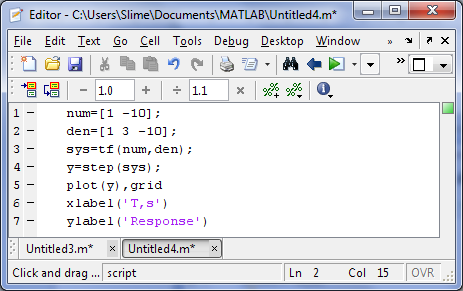
корни

z = 10

p =

-5

2

---

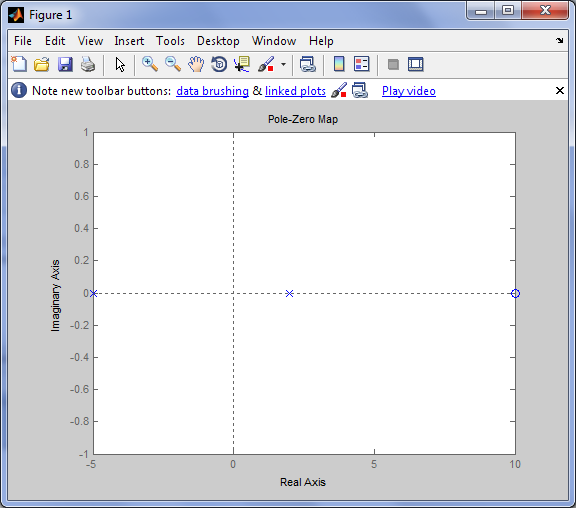
График расположения корней на комплексной плоскости.



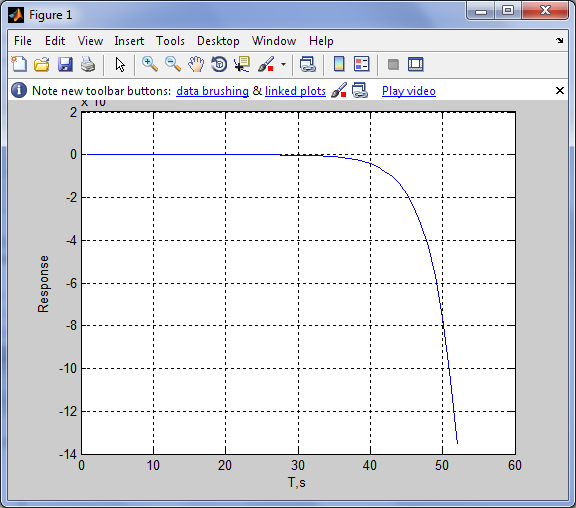
График переходной характеристики объекта (кривая разгона).

Практическая № 2. Исследование устойчивости САР

Задание: провести анализ устойчивости разомкнутой и замкнутой, с единичной обратной связью, системы, заданной дифференциальным уравнением:
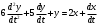. (1)
Выполнение
Если обозначить Y(р) и U(р) как изображения сигналов y и u соответственно, то операторное уравнение (при нулевых начальных условиях) в данном случае примет вид:
.
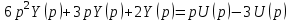Данное уравнение можно преобразовать, вынеся Y(р) и U(р) за скобки:
.
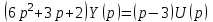Отсюда получаем передаточную функцию разомкнутой системы:
.

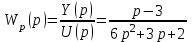Передаточная функция замкнутой системы:
.
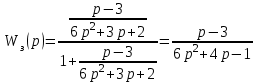Составим скрипт в редакторе M-файлов MATLAB (рисунок 4)


Рисунок 4 – Скрипт в редакторе M-файлов MATLAB
Прямой метод анализа устойчивости.

ans =

-0.2500 + 0.5204i

-0.2500 - 0.5204i

ans =

-0.8604

0.1937

Расположение корней на комплексной плоскости показано на рисунке 5 и 6.


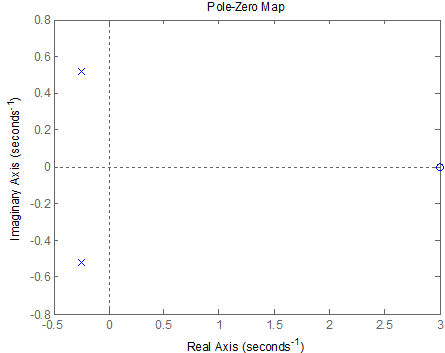
Рисунок 5 – Полюса и нули разомкнутой САР


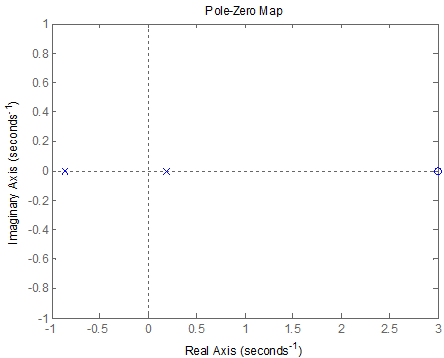
Рисунок 6 – Полюса и нули замкнутой САР
Как видим, все корни разомкнутой системы имеют отрицательные вещественные части, значит, системы устойчива. Один корень замкнутой системы имеет положительную вещественную часть, значит, системы неустойчива.

Критерий Найквиста. Диаграмма Найквиста разомкнутой САУ приведена на рисунке 7


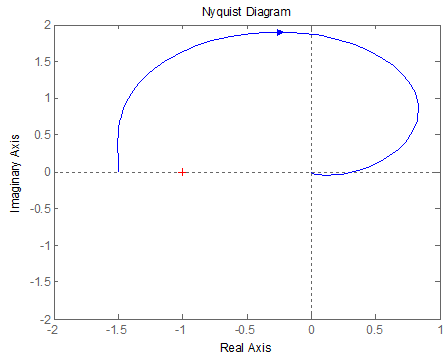
Рисунок 7 – Диаграмма Найквиста разомкнутой САУ

---

Поскольку разомкнутая система устойчива, то для устойчивости замкнутой САУ нужно, чтобы АФЧХ разомкнутой системы не охватывала точку (-1; j0). Как видим годограф Найквиста разомкнутой системы охватывает точку (-1; j0), следовательно, замкнутая система будет неустойчивой.

Критерий Гурвица.

Характеристическое уравнение разомкнутой системы имеет вид:
.
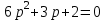Составим определить Гурвица разомкнутой системы и его миноры:

.
;
.
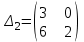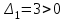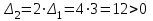Поскольку все миноры положительные, то разомкнутая система устойчива.

Характеристическое уравнение замкнутой системы имеет вид:
.
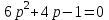Составим определить Гурвица замкнутой системы и его миноры:
.
.
.
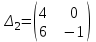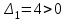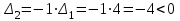Поскольку минор 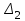отрицательный, то замкнутая система неустойчива.

Список литературы

1. Автоматика и автоматизация систем теплогазоснабжения и вентиляции: Учеб. для вузов / Под ред. В.Н. Богословского . – М. : Стройиздат, 1986. – 479 с.

2. Автоматизация и роботизация строительства: Учеб. пособие / А.Г. Булгаков, В.А. Воробьев, С.И. Евтушенко, Д.Я. Паршин. – 2-е изд. – М. : РИОР : ИНФРА-М, 2013. – 452с.

3. Дьяконов В.П. MATLAB R2006/2007/2008 + Simulink 5/6/7. Основы применения. – 2-е изд., перераб. и доп. – М. : СОЛОН-ПРЕСС, 2008. – 800c.

3. Ившин В.П., Перухин М.Ю. Современная автоматика в системах управления технологическими процессами : Учеб. пособие. – М. : Инфра-М, 2015. – 400с.

4. Кирюшин О.В. Управление техническими системами: курс лекций. – Уфа : Изд-во УГНТУ, 2004. – 171с.

---