ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 43
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Логарифмическое уравнение – это уравнение, в котором переменная содержится под знаком логарифма.
Простейшими логарифмическими уравнениями будем называть уравнение вида:
Это уравнение решается на основании определения логарифма:
Решите простейшее уравнение (решает обучающийся).
4.2 Рассмотрим второй метод решения логарифмических уравнений потенцирование. (Слайд 14)
3. Рассмотрим третий метод решения логарифмических уравнений -введение новой переменной (Слайд 15)
log a x = b, a > 0, a ¹ 1.
Это уравнение решается на основании определения логарифма:
если logaх = b, то x= ab.
Пример 1. Решить уравнение (Слайд 14)
Решение. Область допустимых значений находится из неравенства
ОДЗ: 3х + 1 > 0,
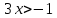 ,
, 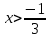 .
. Воспользуемся определением логарифма:
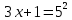 ,
,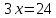 ,
,х=8, принадлежит ОДЗ.
Ответ: 8
Пример 2. Решить уравнение
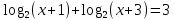
Решение:
Если по каким-либо причинам, мы не можем найти ОДЗ, в конце необходимо сделать проверку.
По свойству логарифмов верно равенство
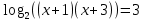 ,
,из этого равенства по определению логарифма получаем
(x+1)(х+3)=8,
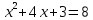 ,
,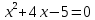 ,
, откуда
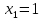 ,
, 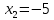 .
.Проверка:
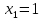 ,
, 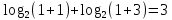 ,
,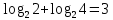 ,
,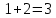 , 3=3.
, 3=3.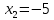 ,
,  ,
,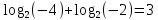 , левая часть уравнения не имеет смысла, поэтому
, левая часть уравнения не имеет смысла, поэтому 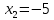 не является корнем этого уравнения.
не является корнем этого уравнения.Ответ:
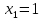
.
Решите простейшее уравнение (решает обучающийся).
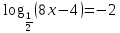 -по определению логарифма решаем
-по определению логарифма решаемОДЗ:8х-4
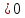
8х-4
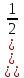
8х-4=
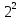
8х=4+4
8х=8
Х=1
Ответ: х=3
4.2 Рассмотрим второй метод решения логарифмических уравнений потенцирование. (Слайд 14)
Суть метода заключается в переходе от уравнения
log a f(x) = log a g(x) к уравнению f(x) = g(x) это и называется потенцированием. При таком методе решения возможно получение посторонних корней. Поэтому из найденных корней уравнения f(x) = g(x) нужно отобрать те, которые принадлежат области определения данного уравнения.
Пример 4. Решить уравнение
log5(2x + 3) = log5(x + 1)
Решение. log5(2x + 3) = log5(x + 1) 2x + 3 = x + 1 x = – 2.
Сделаем проверку: log5(2·(– 2) + 3) = log5(– 2 + 1).
Получаем, что log5(–1) = log5(–1)
С одной стороны, имеем верное равенство, но под знаком логарифма получили число «– 1», какой вывод можем сделать?
Предполагаемый ответ: Под знаком логарифма получили отрицательное число. Но мы знаем, что под знаком логарифма могут стоять только положительные числа.
Преподаватель: Да, так как область определения логарифмической функции – множество всех положительных чисел, то x = – 2 не является корнем данного уравнения. И в ответе запишем, что корней нет.
Решить уравнение методом потенцирования
log1/2(3x-1)=log1/2(6x+8) .
Решение
log1/2(3x-1)=log1/2(6x+8).
О.Д.З.
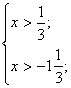
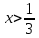
Используя теорему о равенстве логарифмов с одинаковыми основаниями, получаем:
3х-1=6х+8,
-3х=9,
x=-3, не принадлежит ОДЗ, т.е. посторонний корень.
Ответ: нет корней.
3. Рассмотрим третий метод решения логарифмических уравнений -введение новой переменной (Слайд 15)
Рассмотрим логарифмическое уравнение, которое введением новой переменной приводится к квадратному.
Уравнения вида
где a > 0, a ¹ 1, A, В, С – действительные числа.
Пусть t = loga f(x), tÎR. Уравнение примет вид Аt2 + Bt + C = 0.
Решив его, найдём х из подстановки t = loga f(x). Учитывая ОДЗ, выберем только те значения x, которые удовлетворяют неравенству f(x) > 0.
Пример 6. Решить уравнение lg 2 x – lg x – 6 = 0.
Решение. ОДЗ интервал (0; ¥).Введём новую переменную t = lg x, tÎR.
Уравнение примет вид t 2 – t – 6 = 0. Его корни t1 = –2, t2 = 3.
Вернёмся к первоначальной переменной lg x = –2 или lg x = 3,
х = 10 –2 или х = 10 3. Оба значения x удовлетворяют ОДЗ данного уравнения (х > 0).
Ответ. х = 0,01; х = 1000.
Решить уравнение методом введения новой переменной (решает студент):
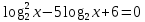
Решение. ОДЗ интервал (0; ¥).Введём новую переменную t = lоg2 x, tÎR.
Уравнение примет вид t 2 –5t + 6 = 0. Его корни t1 = 2, t2 = 3.
Вернёмся к первоначальной переменной lоg2 x = 2 или lоg2 x = 3,
х = 22 или х = 2 3. Оба значения x удовлетворяют ОДЗ данного уравнения (х > 0).
Ответ. х = 4; х = 8.
-
Закрепление изученного материала.
5.1. Пройдите по ссылке и выполните задание
Соотнесите уравнение и метод решения
| log 3(2х - 1) = log 3 27 |
| lg 2 х - 3 lg х - 4 = 0 |
| log2(x+5)=3 |
| log23x+5log3x-2=0 |
| log2(x + 3) = log216 |
5.2. Решите устно уравнения: (Слайд 16)
1.
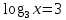 х=27
х=27 2
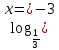
х=27
3.
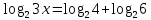 х=8
х=84.
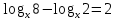 х=2
х=25.3. Самостоятельная работа.
| Вариант 1. | Вариант 2. |
| а) 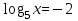 ; ;б) 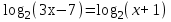 ; ;в) 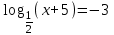 ; ;г) 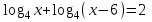 д) 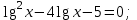 | а) 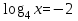 ; ;б) 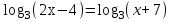 ; ;в) 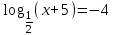 ; ;г) 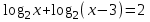 ; ;д) 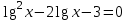 |
VI. Подведение итогов занятия Рефлексия.
Преподаватель: Давайте обобщим сведения, полученные сегодня на занятии. Какие уравнения мы сегодня решали и какие знания нам помогали их решать
VII.Домашнее задание:
1. Работа с конспектом,
2. Решить уравнения, карточки с разноуровневым дом задание. Кто желает может сделать все уровни
| 1 уровень
| 2 уровень
| 3 уровень
|
Преподаватель. И в конце занятия давайте оценим ваши впечатления. Что узнали нового? Было ли интересно, познавательно? Какие возникли трудности в усвоении нового материала? Сложно ли было вам включиться в учебный процесс?
Для этого я предлагаю заполнить «лист самоанализа деятельности обучающегося».
Лист самоанализа деятельности обучающегося
Из предложенных утверждений отметь те, с которыми вы согласны.
 Мне было интересно работать на занятии.
Мне было интересно работать на занятии. Данная тема понятна для меня.
Данная тема понятна для меня. В процессе работы у меня возникли затруднения.
В процессе работы у меня возникли затруднения. Результатом работы я доволен.
Результатом работы я доволен.Поделись впечатлениями о занятии: что понравилось или не понравилось________________________________________________________________________________________________________________________________________________________________________________________.
Рефлексия
-
Дайте оценку своей деятельности на уроке:
- Я работал отлично, в полную силу своих возможностей, Чувствовал себя уверенно.
- Я работал хорошо, но не в полную силу, испытывал чувство неуверенности, боязни, что отвечу неправильно.
- У меня не было желания работать. Сегодня не мой день.
-
С каким настроением вы уходите с урока?
Приклейте на свою оценочную карту стикер соответствующего цвета (прием «Светофор»):
- красный- тревожно, тему не понял;
- желтый- спокоен, скорее понял, чем нет:
- зеленый- понял всю тему, уверен, что смогу решить самостоятельную работу.