Файл: Спецглавы теоретических основ теплотехники Богомолов А. Р.docx

Спецглавы теоретических основ теплотехники Богомолов А.Р.

1. Теплоемкость, теплопроводность и температуропроводность тел.

Т еплоёмкость -  количество теплоты, поглощаемой телом при нагревании на 1 градус; точнее — отношение количества теплоты, поглощаемой телом при бесконечно малом изменении его температуры, к этому изменению Т. единицы массы вещества (г, кг) называется удельной теплоёмкостью, 1 моля вещества — мольной (молярной) Т.
Теплопрово́дность — способность материальных тел проводить энергию от более нагретых частей тела к менее нагретым частям тела путём хаотического движения частиц тела

Теплопроводностью называется также количественная характеристика способности тела проводить тепло.

Температуропрово́дность (коэффицие́нт температуропрово́дности) — физическая величина, характеризующая скорость изменения температуры вещества в неравновесных тепловых процессах. Численно равна отношению теплопроводности к удельной теплоёмкости при постоянном давлении.

2. Смеси идеальных газов

Смесь идеальных газов — это идеальный газ, каждый из компонентов которого равномерно распределен по всему объему, занимаемому газом.

Смесь идеальных газов подчиняется уравнению Менделеева — Клапейрона (уравнению состояния), которое записывается в традиционной форме:

pV = νRT,

где p — давление смеси газов; V — объем, занимаемый смесью газов; ν — количество вещества в смеси газов; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T — температура смеси идеальных газов.

Давление смеси идеальных газов вычисляется при помощи закона Дальтона:

p = p ₁ + p ₂ + ... + p _n ,

где p ₁, p ₂, ..., p _n  — парциальные давления компонентов смеси, т.е. давления, которые бы оказывал каждый из компонентов смеси газов при условии, что он занимает весь объем.

Давления каждого из компонентов смеси определяются следующим образом:

• 
  давление первого компонента смеси
  

---

p1=ν1RTV;

• 
  давление второго компонента смеси
  

p2=ν2RTV; ...

• 
  давление n-го компонента смеси
  

pn=νnRTV,

где ν₁ — количество вещества первого компонента смеси; ν₂ — количество вещества второго компонента смеси, ...; ν _n  — количество вещества n-го компонента смеси; R — универсальная газовая постоянная, R ≈ 8,31 Дж/(моль ⋅ К); T — температура смеси; V — объем сосуда, заполненного смесью газов (объем смеси).

Средняя молярная масса смеси рассчитывается по формуле

⟨M⟩=mν,

где m — масса смеси газов; ν — количество вещества в смеси газов.

Масса смеси газов складывается из масс его компонентов:

Количество вещества в смеси газов определяется как сумма количеств вещества каждого из компонентов:

ν = ν₁ + ν₂ + ... + ν _n ,

количество вещества первого компонента смеси —

ν1=m1M1,

3. Диффузия

Диффузией называют самопроизвольный процесс, стремящийся к установлению внутри фаз равновесного распределения концентраций. В однородной по температурам и давлениям смеси процесс диффузии направлен к выравниванию концентраций в системе. При этом, происходит перенос вещества из области с большей в область с меньшей концентрацией.

Диффузия, обусловленная градиентом концентрации компонента, называется концентрационной диффузией. Аналогично теплообмену диффузия (массообмен) может происходить как молекулярным (микроскопическим), так и молярным (макроскопическим или конвективным) путем.

В газах молекулярная диффузия осуществляется за счет теплового движения молекул.

Диффузия характеризуется потоком массы компонента, т.е. количеством вещества, проходящим в единицу времени через поверхность в направлении нормали к ней. Поток массы J, кг/с. Плотностью потока массы j называют поток массы, проходящий через единицу поверхности:

3. Конвективный теплообмен

Если газ (или жидкость) вступает в контакт с поверхностью твердого тела, имеющий другую температуру, то протекающий процесс обмена тепловой энергией называется конвективным теплообменом.

Перенос теплоты осуществляется одновременно конвекцией и теплопроводностью. Под конвекцией теплоты понимают перенос теплоты при перемещении макрочастиц жидкости или газа в пространстве из области с одной температурой в область с другой. Конвекция возможна только в текучей среде, здесь перенос теплоты связан с переносом самой среды.

---

3. Физические свойства жидкостей и газов

Плотность-распределение массы по занимаемому объему. Удельный вес-вес в занимаемом объеме. Плотность смеси равна сумме произведений плотностей отдельных газов, взятых при давлении и температуре смеси, на их объемные или мольные доли.

Сжимаемость-свойство изменять свой объем при изменении давления. Вязкость-свойство сопротивляться сдвигу (или скольжению) слоев.



Поверхностное натяжение – свойство, обуславливающееся силами взаимного притяжения, возникающая между частицами поверхностного слоя и вызывающими напряжение состояния.

3. Закон сохранения энергии для движущийся среды

3. 8. Антоху спросим

9. Дифференциальное уравнение переноса массы.

Молекулярная диффузия в неподвижной среде протекает медленно. Наибольший практический интерес представляет перенос вещества не только за счет молекулярной диффузии, но и за счет перемещения самого элемента в пространстве. Такая диффузия называется конвективной:

10. Система уравнений для турбулентного движения жидкости

Турбулентное движение жидкости - неупорядоченное движение, при котором отдельные частицы жидкости движутся по запутанным, хаотическим траекториям, в то время как вся масса жидкости в целом перемещается в одном направлении.

Какой будет вид движения – турбулентный или ламинарный – зависит от критерия Рейнольдса Re.

---

11. Условия однозначности для процессов конвективного теплообмена

(Оно же – краевые условия)

Чтобы из бесчисленного количества выделить конкретно рассматриваемый процесс и дать его полное математическое описание, к дифференциальному уравнению необходимо присоединить математическое описание всех частных особенностей рассматриваемого процесса. Эти частные особенности, которые совместно с дифференциальным уравнением дают полное математическое описание конкретного процесса теплопроводности, называются условиями однозначности или краевыми условиями. Математическое описание дает возможность нахождения распределения температур в теле для конкретных условий распространения тепла.

Разделяется на: геометрические, физические, начальные (временные) и граничные условия.

* Геометрическими условиями задаются форма и размеры тела, в котором протекает процесс.

* Физическими условиями задаются физические параметры тела и среды, например, λ, с, ρ.

* Начальные условия – для создания закона распределения температуры до нагревания тела

t = f (x, y, z ).

В случае равномерного распределения температуры в теле: t = t0 = const.

Граничное условие 1 рода. Задается распределение температуры на поверхности тела для каждого момента времени:

tc = f (x, y, z, τ),

Граничное условие 2 рода. Задаются значения теплового потока для каждой точки поверхности тела и любого момента времени:

qc = f (x, y, z, τ),

Граничное условие 3 рода. Задаются температура и закон теплообмена между телом и окружающей средой. Описывается законом Ньютона-Рихмана:

q = α (tc - toc)

Граничное условие 4 рода. Теплообмен между двумя твердыми телами, между телами идеальный контакт и температуры соприкасающихся поверхностей равны.

Предполагается равенство тепловых потоков через поверхность соприкосновения.

В таких задачах задается отношение тангенсов угла наклона касательных к температурным кривым.



Или

12. Значения теории подобия. Условия подобия физических явлений.

Теория подобия - учение об условиях подобия физических явлений. Теория подобия опирается на учение о размерностях физических величин и служит основой моделирования физического. Предметом Т.п. является установление подобия критериев различных физических явлений и изучение с помощью этих критериев свойств самих явлений.

---

Условия подобия:

а) Понятие подобия в отношении физических явлений приме­нимо только к явлениям одного и того же рода, которые качест­венно одинаковы и аналитически описываются одинаковыми урав­нениями как по форме, так и по содержанию.

б) Обязательной предпосылкой подобия физических явлений должно быть геометрическое подобие. Последнее означает, что подобные явления всегда протекают в геометрически подобных си­стемах.

в) При анализе подобных явлений сопоставлять между собой можно только однородные величины и лишь в сходственных точ­ках пространства и в сходственные моменты времени.

г) Наконец, подобие двух физических явлений означает подо­бие всех величин, характеризующих рассматриваемые явления. Это значит, что в сходственных точках пространства и в сходственные моменты времени любая величина φ' первого явления пропорциональна однородной с ней величине φ" второго явления, т. е. φ" = сφ φ'.

13. Критерии подобия и уравнения конвективного теплообмена:

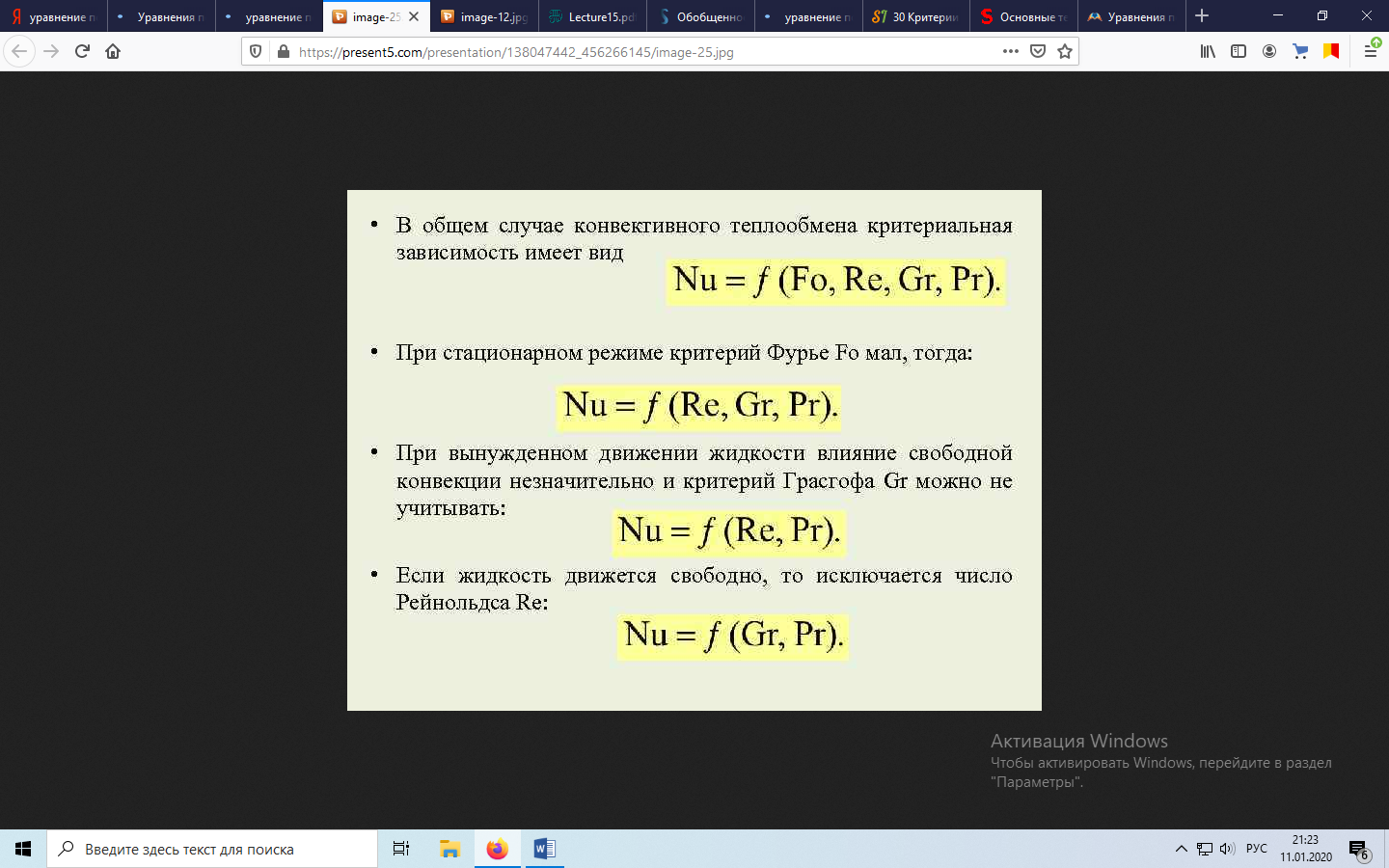
13. Основы теории пограничного слоя. Особенности течения вязкой жидкости при больших числах Re. Пограничный слой.

Основы теории пограничного слоя:

При обтекании твердого тела влияние сил вязкости может быть существенным только в области тонкого пристеночного слоя, а за его пределами им можно пренебречь. В основной массе потока (вдали от стенки) скорости жидкости в значительной мере выравнены по сечению трубы однако вблизи стенки трубы скорость резко снижается, обращаясь у самой стенки в нуль. В непосредственной близости от стенки, с приближением к ней, движение жидкости становится все менее турбулентным и все более ламинарным, вследствие того, что твердая стенка как бы «гасит» турбулентные пульсации в поперечном направлении. Таким образом, турбулентное движение не существует в чистом виде, а всегда сопровождается ламинарным. Условно различают центральную зону, или

---