Файл: Контрольная работа учебнометодическое пособие Новосибирск 2021.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 198
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации
Федеральное государственное бюджетное образовательное
учреждение высшего образования
Сибирский государственный университет
телекоммуникаций и информатики
Е.В. Кокорева
Программно конфигурируемые сети
Анализ эффективности
Контрольная работа
учебно-методическое пособие
Новосибирск 2021
Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации
Федеральное государственное бюджетное образовательное
учреждение высшего образования
"Сибирский государственный университет
телекоммуникаций и информатики"
Е.В. Кокорева
ПРОГРАММНО КОНФИГУРИРУЕМЫЕ СЕТИ
АНАЛИЗ ЭФФЕКТИВНОСТИ
Контрольная работа
УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ
Новосибирск 2021
УДК 621.391
КокореваЕ.В. Программно конфигурируемые сети. Анализ эффективности: учебно-методическое пособие. – Новосибирск: СибГУТИ, 2021. – 26 c.
Учебно-методическое пособие предназначено для подготовки студентов направления 11.03.02 «Инфокоммуникационные технологии и сети связи». В пособии приведена методика расчёта характеристик программно конфигурируемой сети при помощи аналитической модели в виде замкнутой однородной сети массового обслуживания.
Кафедра
Таблиц – 3, иллюстраций – 6, литературы – 6 наим.
Рецензент – доцент кафедры телекоммуникационных сетей и вычислительных средств О.И. Моренкова
Утверждено редакционно-издательским советом СибГУТИ в качестве учебно-методического пособия.
© Сибирский государственный университет
телекоммуникаций и информатики, 2021
Оглавление
VII Метод анализа средних значений 16
Контрольные вопросы 24
Замечания по выполнению и оформлению контрольной работы
-
Выполнение контрольной работы
Контрольная работа требует для своего выполнения наличия на компьютере пакета математических и инженерных расчётов, такого как Mathcad или SMath Studio. Рекомендуется использование последнего из них,
т.к. данный пакет является свободно распространяемым, легко устанавливается на компьютер и не требует каких-либо специальных знаний для его использования.
Вариант задания выбирается из таблицы 1 (ячейка таблицы содержит номер варианта, соответствующие заголовки строки и столбца – исходные данные для расчёта) по двум последним цифрам пароля. Если число, образованное двумя последними цифрами пароля, превышает 25, то в качестве номера варианта принимается сумма этих цифр.
Преподаватель должен получить от студента на проверку архив, содержащий два документа:
-
Отчёт в виде текстового документа (.doc, .docx или .pdf). -
Файл рабочий лист Mathcad в формате .mcd, .xmcd или рабочий лист SMath Studio в формате .sm с расчётами и графиками.
-
Оформление отчёта
Отчёт по выполнению контрольной работы должен быть оформлен в соответствии с ГОСТ 2.105-95, ГОСТ 7.32-2017, ГОСТ Р 2.105-2019 и содержать:
-
Титульный лист. -
Аннотацию. -
Содержание (с нумерацией страниц). -
Задание в соответствии с вариантом. -
Краткое теоретическое описание моделируемой системы.
П
-
Выполнение задания с описанием основных этапов. -
Результаты выполнения в виде графиков зависимостей, полученных в ходе расчёта. -
Выводы по проделанной работе. -
Список литературы (по ГОСТ 7.1-2019).
Рисунки (графики, схемы, диаграммы и пр.), таблицы, формулы и другие объекты должны быть пронумерованы и подписаны в соответствии с ГОСТ 2.105-95.
Введение
Программно-конфигурируемая сеть (SDN от англ. Software-Defined Networking) – сеть передачи данных, в которой уровень управления сетью отделён от устройств передачи данных и реализуется программно [1].
Физически сеть строится из тех же основных компонентов, что и традиционные телекоммуникации: контроллера, маршрутизаторов, коммутаторов, концентраторов, абонентских устройств, соединяемых друг с другом проводными и беспроводными линиями связи.
Аналитическое моделирование позволяет получить и оценить показатели качества обслуживания ТКС, такие как интервал задержки, вероятность потерь, коэффициент загрузки сети и пр.
При выполнении контрольной работы необходимо построить математическую модель замкнутой однородной сети массового обслуживания (СеМО) в соответствии с заданной топологией инфокоммуникационной сети, определить маршрутную матрицу, предположив, что все направления передачи равновероятны.
Требуется получить и проанализировать вероятностно-временные характеристики данной сети, используя метод анализа средних значений MVA (англ. Mean Value Analysis).
Теоретическая часть
I Определение сети массового обслуживания
Сеть массового обслуживания (СеМО) – это совокупность систем массового обслуживания (СМО) с различными интенсивностями обслуживания, в которой циркулирует некоторое количество заявок различных классов, обсуживаемых в соответствии с заданной дисциплиной [2].
Понятие СеМО ввёл в обращение Дж. Р. Джексон в 1957 г. в статье “Networks of Waiting Lines”. Пример СеМО, являющейся моделью компьютерной системы, можно видеть на рис. 1.
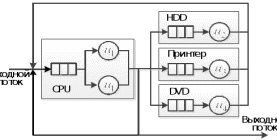
Рис. 1. Пример сети массового обслуживания
Заявки поступают в систему в разных точках, ждут в очереди обслуживания и, покинув один узел, поступают в другой для дальнейшего обслуживания в соответствии с маршрутной матрицей
 .
.Пример маршрутной матрицы [2]:
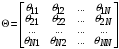 , (1)
, (1)где
 – вероятность перехода заявки из i-го узла в j-й узел; N – количество узлов СеМО.
– вероятность перехода заявки из i-го узла в j-й узел; N – количество узлов СеМО.Маршрутная матрица определяет топологию сети массового обслуживания, и для неё должны выполняться условия стохастичности:
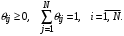 (2)
(2)Дисциплины обслуживания, принятые в теории сетей массового обслуживания:
-
FCFS (англ. FirstCome, FirstServed) – первым пришёл, первым обслужился или обслуживание в порядке поступления; -
LCFS (англ. LastCome, FirstServed) – последним пришёл, первым обслужился; -
LCFS-PR (англ. LastCome, FirstServed – PreemptiveResume) – последним пришёл, первым обслужился с прерыванием и дообслуживанием; -
PS (англ. ProcessorSharing) – равномерное распределение пропускной способности между заявками; -
IS (англ. InfiniteServers) – бесконечное количество обслуживающих приборов; -
FS (англ. FiniteServers) – конечное число обслуживающих приборов.
II Классификация CeMO
Можно привести классификацию СеМО по следующим критериям [3]:
1. По наличию внешнего источника и стока заявок:
– открытые;
– замкнутые;
– смешанные.
Открытой называется СеМО (ОСеМО), имеющая бесконечный внешний источник заявок и сток, в который заявки уходят из сети после обслуживания. Как поступление заявок в сеть, так и уход может осуществляться через любой узел. В каждый момент времени в открытой СеМО может находиться произвольное число заявок.
В замкнутой СеМО (ЗСеМО) отсутствуют источник и сток, и количество циркулирующих в ней заявок постоянно. Пример замкнутой СеМО изображён на рис. 9.2. Заметим, что открытая СеМО легко преображается в замкнутую введением дополнительного узла, обозначающего источник-сток заявок.
Смешанные СеМО обладают свойствами открытых и замкнутых сетей одновременно. Например, для заявок одного класса сеть является замкнутой, а для заявок других классов – открытой.
2. По числу классов заявок:
– однородные;
– неоднородные.
Для полного описания СеМО необходимо определить понятие класса заявок. Класс заявок – множество требований с одинаковыми свойствами, т.е. имеющими одинаковые маршруты, одинаковые распределения времени обслуживания и одни и те же приоритеты. Если заявки различаются хотя бы одним из этих параметров, они принадлежат разным классам. По окончании обработки в некотором узле, требование может перейти не только в другой узел, но и в другой класс, изменив свои свойства. Например, запрос, дойдя до обслуживающего сервера, превращается в информационный пакет, который в свою очередь, дойдя до запрашивающего клиента, превращается в квитанцию.
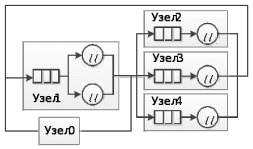
Рис. 2. Пример замкнутой СеМО
Однородными называются сети, в которой существует только один класс заявок, а неоднородными – сети с более чем одним классом заявок.
Для простоты далее будем рассматривать однородные СеМО.
3. По распределению времени обслуживания:
– марковские;
– общего вида.
Марковские (экспоненциальные) СеМО характеризуются показательным распределением времени обслуживания для каждого обслуживающего прибора, входящего в сеть и в случае открытых сетей – показательным распределением промежутков времени между поступлениями заявок. Сети, в которых хотя бы один прибор обладает распределением времени обслуживания, отличным от показательного, называются СеМО
общего вида.
III Марковские СеМО. Теорема Берке
Рассмотрим простейшую последовательную систему (сеть обслуживания), состоящую двух узлов (рис. 3) [4].

Рис. 3. Сеть с двумя последовательными узлами
Каждый овал на рис. 3 обозначает СМО с показательно распределённым временем обслуживания с одинаковым параметром µ (внутри овала указан номер узла: узел_1, узел_2).
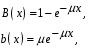
 . (3)
. (3)Входящий в систему поток заявок является пуассоновским с параметром :
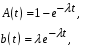
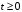 . (4)
. (4)Задача состоит в том, чтобы определить распределение промежутков времени между последовательными заявками, поступающими в узел_2, что эквивалентно задаче нахождения распределения промежутков времени между последовательными заявками, выходящими из узла_1.
Обозначим
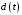 – плотность распределения вероятностей промежутков между последовательными заявками на выходе узла_1 и
– плотность распределения вероятностей промежутков между последовательными заявками на выходе узла_1 и 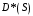 – преобразование Лапласа этой величины. Вычислим
– преобразование Лапласа этой величины. Вычислим 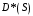 в момент, когда требование покидает узел_1. Возможно одно из двух событий: либо в очереди имеется вторая заявка, готовая поступить в прибор узла_1, либо нет (накопитель пуст). В первом случае промежуток времени, через которое второе требование покинет узел_1, распределён так же, как время обслуживания, и в этом случае получаем:
в момент, когда требование покидает узел_1. Возможно одно из двух событий: либо в очереди имеется вторая заявка, готовая поступить в прибор узла_1, либо нет (накопитель пуст). В первом случае промежуток времени, через которое второе требование покинет узел_1, распределён так же, как время обслуживания, и в этом случае получаем: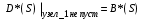 . (5)
. (5)Во втором случае промежуток времени, через который следующая заявка покинет узел_1, складывается из двух промежутков:
1) время до поступления следующей заявки;
2) время обслуживания следующей заявки.
Так как эти два промежутка распределены независимо, то плотность распределения вероятностей их суммы равна свёртке плотностей распределения суммируемых величин.
Преобразование Лапласа плотности распределения суммы независимых случайных величин равно произведению преобразований исходных плотностей распределения.