Файл: Контрольная работа учебнометодическое пособие Новосибирск 2021.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 205
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
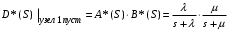 . (6)
. (6)В выражении (6) первый и второй сомножители правой части представляют собой преобразования Лапласа показательной функции.
Кроме того, вероятность того, что заявка покинет систему пустой равно вероятности того, что поступающее требование застанет систему пустой.
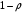 , где – коэффициент загрузки системы.
, где – коэффициент загрузки системы.Запишем безусловное преобразование Лапласа для плотности распределения промежутков времени между уходящими требованиями:
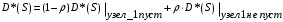 . (7)
. (7)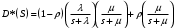 . (8)
. (8)Упрощаем:
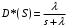 (9)
(9)Обратное преобразование дает нам:
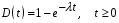 (10)
(10)Таким образом, доказано, что промежутки времени между уходящими требованиями, также как и промежутки времени между поступающими требованиями распределены показательно с тем же параметром (интенсивность входящего потока, с-1).
Теорема Берке: В случае стационарной СМО входящий пуассоновский поток, проходя через обслуживающий прибор с показательным распределением, порождает выходящий пуассоновский поток с тем же параметром.
Теорема Берке справедлива для стационарной СМО М/М/m с дисциплиной обслуживания «Первый пришёл – первый обслужился» FCFS.
IV Параметры СеМО
Для анализа СеМО необходимо задать её параметры, которые могут различаться в зависимости от вида СеМО [5].
4.1 Параметры однородной СеМО
Полное описание однородной сети массового обслуживания требует задания параметров, приведённых в таблице 1.
Таблица 1. Параметры СеМО
| Параметр | Описание |
| Общие параметры | |
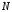 | количество СМО (узлов); |
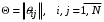 | матрица вероятностей переходов (маршрутная матрица); |
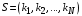 | состояние СеМО; |
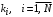 | количество заявок в i-й СМО; |
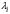 | интенсивность поступления заявок в i-й узел из других узлов (и из внешнего источника в ОСеМО); |
| Параметры открытой СеМО | |
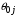 | вероятность поступления заявки извне через j-й узел; |
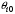 | вероятность ухода заявки из СеМО через i-й узел; |
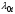 | интенсивность поступления заявок извне через i-й узел; |
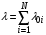 | интенсивность поступления заявок в СеМО; |
| Параметры замкнутой СеМО | |
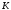 | фиксированное число заявок, циркулирующих в ЗСеМО; |
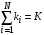 | сумма заявок, находящихся в каждой СМО. |
Интенсивности потоков поступающих заявок определяются решением систем уравнений, которые приведены ниже.
Уравнения равновесия потоков:
– для ОСеМО:
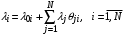 ; (11)
; (11)– для ЗСеМО:
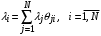 . (12)
. (12)Полезной для дальнейшего анализа характеристикой является среднее количество переходов заявки в узел i (коэффициент переходов):
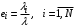 . (13)
. (13)Из выражений (9.9)–(9.11) можно получить:
– для ОСеМО:
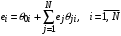 ; (14)
; (14)– для ЗСеМО:
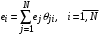 . (15)
. (15)Используя коэффициент переходов, можно получить относительный коэффициент использования:
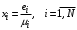 . (16)
. (16)4.2 Параметры неоднородной СеМО
В таблице 2 приведены параметры неоднородной СеМО, отличающие её от однородной.
Таблица 2. Параметры неоднородной СеМО
| Параметр | Описание |
| Общие параметры | |
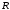 | количество классов заявок СеМО; |
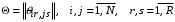 | маршрутная матрица; |
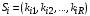 | состояние i-й СМО; |
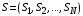 | состояние СеМО; |
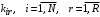 | количество заявок r-го класса в i-й СеМО; |
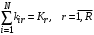 | количество заявок r-го класса в СеМО; |
| Параметры замкнутой СеМО | |
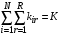 | сумма заявок всех классов в ЗСеМО. |
Остальные параметры (интенсивности входящих потоков, интенсивности обслуживания, коэффициенты переходов и пр.) несут тот же смысл, что и в однородной сети с учётом класса заявки
r.
Далее для простоты будем рассматривать характеристики однородных СеМО.
V Характеристики СеМО
Важнейшей характеристикой, отправной точкой для анализа параметров СеМО является распределение вероятностей её состояний:
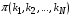 [5].
[5].С вероятностями состояний СеМО связаны следующие характеристики:
1. Маргинальная вероятность того, что количество заявок в i-м узле
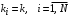 :
: ; (17)
; (17)Заметим, что:
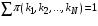 . (18)
. (18)При этом для ЗСеМО выполняется:
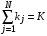 . (19)
. (19)2. Коэффициент использования прибора в i-м узле для одноканальной СМО:
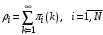 . (20)
. (20)Этот параметр может интерпретироваться как вероятность того, что прибор i-го узла занят обслуживанием:
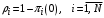 . (21)
. (21)Для многоканальной СМО:
 . (22)
. (22)Если интенсивность обслуживания не зависит от нагрузки, то коэффициент использования:
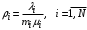 . (23)
. (23)3. Интенсивность потока, входящего в i-й узел в общем случае, если интенсивность обслуживания зависит от нагрузки:
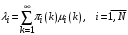 . (24)
. (24)Если интенсивность обслуживания не зависит от нагрузки:
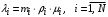 . (25)
. (25)4. Пропускная способность замкнутой СеМО:
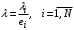 . (26)
. (26)5. Среднее количество заявок в i-м узле:
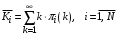 . (27)
. (27)По теореме Литтла [4]:
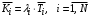 , (28)
, (28)отсюда среднее время реакции:
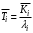 . (29)
. (29)6. Средняя длина очереди:
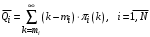 . (30)
. (30)По теореме Литтла:
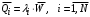 , (31)
, (31)отсюда среднее время ожидания обслуживания:
 . (32)
. (32)VI Сети Джексона
Джексон доказал, что распределение вероятностей состояний СеМО может быть получено в мультипликативной форме [4]:
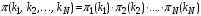 . (33)
. (33)При этом для конкретных СМО
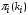 может быть определена по известным формулам теории массового обслуживания [4]. Например, для СМО типа M/M/1:
может быть определена по известным формулам теории массового обслуживания [4]. Например, для СМО типа M/M/1: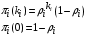 , (34)
, (34)а для СМО типа M/M/m:
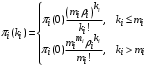 , (35)
, (35)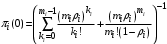 . (36)
. (36)Пример 1:
Рассмотрим ОСеМО, приведённую на рис. 4.

Рис. 4. Открытая СеМО для расчёта характеристик
Исходные данные:
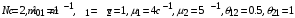 .
.Требуется найти вероятности состояний
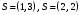 .
.Для нахождения интенсивностей потоков воспользуемся выражением (11):
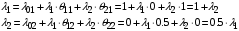 .
.Решение:
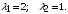
Коэффициенты загрузки:
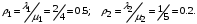
Маргинальные вероятности по ф. (34):
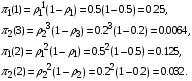
Вероятности заданных состояний по ф. (33):
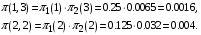
По ф. (21)–(32) вычисляются другие узловые и сетевые характеристики.
VII Метод анализа средних значений
Как следует из названия, метод применяется для вычисления средних значений характеристик СеМО, таких как среднее время реакции, среднее количество заявок, коэффициент загрузки, коэффициент простоя и др. [6].
MVA (англ. Mean-Variance Analysis) метод базируется на:
1. Формуле Литтла [4], выражающей среднее количество заявок в системе через интенсивность входящего потока заявок и среднее время пребывания заявки в системе:
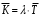 . (37)
. (37)2. Теореме распределения по времени поступления (англ. Theoremofthedistributionatarrivaltime) или в сокращении теорема поступления, утверждающей, что если рассматривать i-й узел замкнутой марковской СеМО с k заявками в момент поступления в него новой заявки, стационарная вероятность состояния этого узла совпадает со стационарной вероятностью его состояния при наличии
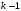 заявок в сети.
заявок в сети.
Теорема поступления позволяет рекуррентно вычислить среднее время пребывания заявки в i-м узле. Его значение будет складываться из среднего времени обслуживания всех
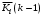 ранее поступивших заявок и среднего времени обслуживания текущей заявки:
ранее поступивших заявок и среднего времени обслуживания текущей заявки:– для одноканальной системы с дисциплинами обслуживания FCFS, LCFS-PR, PS:
 ; (38)
; (38)– для многоканальной системы необходимо ещё учитывать условные вероятности
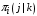 :
: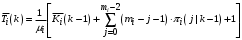 ; (39)
; (39)где
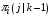 – вероятность того, что в i-й СМО содержится j заявок, при условии, что в СеМО циркулирует
– вероятность того, что в i-й СМО содержится j заявок, при условии, что в СеМО циркулирует  заявок.
заявок.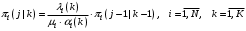 , (40)
, (40)где
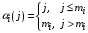 .
.– для СМО с дисциплиной обслуживания IS:
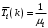 . (41)
. (41)Определив среднее время пребывания заявки в СМО, определяем среднее время пребывания заявки в СеМО:
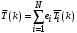 . (42)
. (42)По формуле Литтла ф. (37) пропускная способность системы:
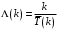 . (43)
. (43)Интенсивности потоков, входящих в i-е узлы:
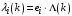 . (44)
. (44)Среднее количество заявок в каждом узле:
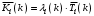 . (45)
. (45)Начальными условиями для расчёта являются:
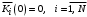 ,
,и дополнительно для многоканальных СМО:
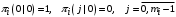 .
.Расчёт повторяется для
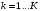 .
.Пример 2:
Для примера рассмотрим модель на рис. 5 с исходными данными:
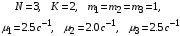 .
.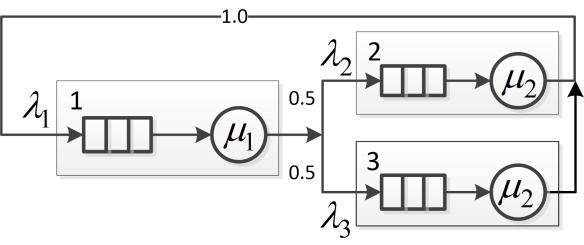
Рис. 5. Замкнутая СеМО для расчёта характеристик
Маршрутная матрица:
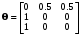 .
.Все возможные состояния СеМО: