Файл: paper.doc

The paper addresses the problem of output feedback controller design for linear continuous and discrete-time systems using non-iterative linear matrix inequality (LMI) procedure with guaranteed cost. Numerical examples are given to illustrate the effectiveness of the proposed methods.

K e y w o r d s: output feedback controller design, LMI

1 Introduction

The static output feedback problem is one of the most important open questions in control engineering, [13].Several solutions to this problem are available. The necessary and sufficient conditions for static output feedback stabilizability of linear continuous or discrete-time systems are given in [6] and [10] with iterative procedure to output feedback controller design. An approach based on linear- quadratic regulator theory applying Lyapunov results to output stabilization was presented in [7] for continuous-time systems leading to an iterative solution of three coupled matrix equations. Iterative LMI based output feedback controller design using structurally constrained state feedback approach was developed in [14]. Output feedback stabilization of discrete-time systems employing LQ regulator theory [9], [8], [5] can be found in [3]. Robust static output feedback controller design procedure have been proposed in large number of references. Basically, in most of them the linearization approach [4] is used to obtain a stabilization controller. In the above papers the existence of output feedback controller solution or convergence of the proposed algorithms are not discussed. In this paper a non-iterative (non-linearization) approach to design of output feedback controller employing LQ theory with guaranteed cost is proposed for some class of linear continuous and discrete-time systems. The proposed approach is based on the LMI novel necessary and sufficient stability conditions for linear systems.

2 Problem formulation and preliminaries

Consider a linear time invariant system:

(1)

where

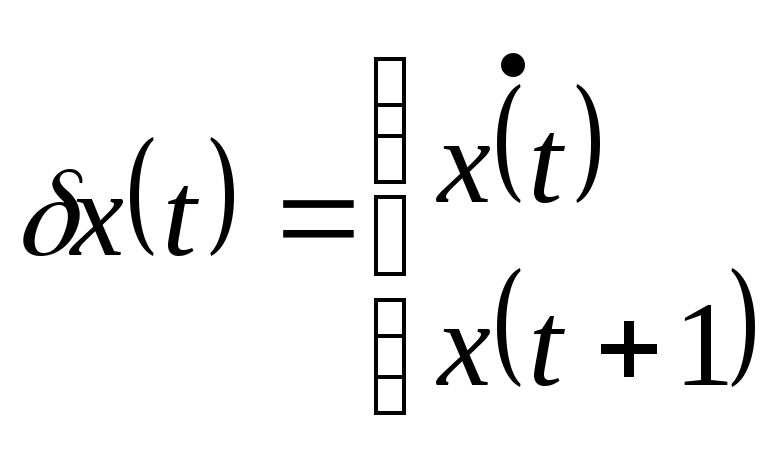
are state, control and output vectors, respectively; A,B,C are constant matrices of appropriate dimensions.

The feedback control law is considered in the form

(2)

where F is a static output feedback controller gain matrix. The closed-loop system is then

(3)

where

As is well known, the fixed order dynamic output feedback control design problem is a special case of the static output feedback problem, since the closed-loop system for the fixed order case has exactly the same structure as the static case with appropriately augmented system matrices [5]. To assess the performance quality a quadratic cost function known from LQ theory is often used. However, in practice the response rate or overshoot are often limited. Therefore we include into the LQR cost function the additional derivative term for state variable to open the possibility to damp the oscillations and limit the response rate.

(4)

for continuous-time and

(5)

for discrete-time systems.

Definition 1. Consider the system (1). If there exists a control law and a positive scalar such that the closed loop system (3) is stable and the closed loop value cost function (4) or (5) satisfies then is said to be guaranteed cost and is said to be the guaranteed cost control law for system (1). For continuous and discrete-time systems the following theorem holds.

Theorem 1 (Discrete-time systems). Consider system (1) and cost function (5) with , then the following statements are equivalent:

• Closed loop system (3) is static output feedback stabilizable with guaranteed cost

(6)

where is a real symmetric positive definite matrix.

• The pairs (A,B) is stabilizable, (A,C) is detectable and there exist real matrices F and such that

(7)

where P is solution of

(8)

• There exist positive definite matrices P,R,Q and matrix F such that

(9)

Proof of theorem is given in [10].

Similar theorem there is for continuous-time system [6]. For continuous-time systems (7), (8) and (9) read as follow:

In [13] it is presented that the problem of static output feedback is still open. Various unconnected necessary conditions, sufficient conditions and ad hoc solution techniques abound. The so-called necessary and sufficient conditions [6], [10] are not testable, and as such only succeed in transforming the problem into another unsolved problem or into a numerical search problem with no guarantee of convergency to a solution. The recent indications that the output feedback problem may be N-P hard implies that moderately large problems are computationally intractable. In this paper we have proposed new conditions for stability analysis and sufficient conditions for static output feedback stabilizable with guaranteed cost which is suitable for LMI non-iterative solution.

3 Static output feedback controller design

In this paragraph we present new procedures for stability analysis of system (1) and to design of static output feedback for continuous and discrete-time systems (3) with control law (2) which ensure the guaranteed cost for closed loop system. The main results for continuous-time system are summarized in the following theorem.

Theorem 2. Consider linear system (1) with static output feedback (2) and cost function (4). The following statements are equivalent:

(i) Closed loop system (3) is asymptotically stable with guaranteed cost with respect to cost function (4)

(ii) There exist positive definite matrices P,R,Q, positive (semi) definite matrix S and matrix F such that

(10)

where k > 0 is some positive constant.

(iii) There exist positive definite matrices P,R,Q, positive (semi) definite matrix S and matrices F and M such that

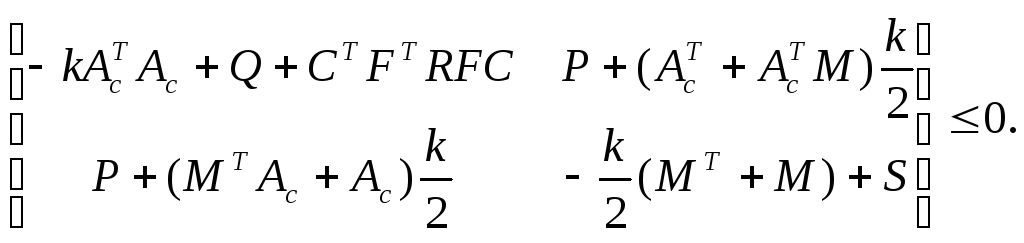(11)

P r o o f . Suppose(11) holds. Equation (11) can be rewritten as follows

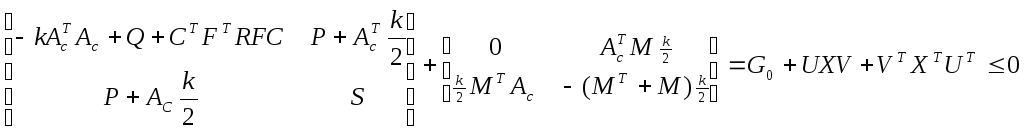(12)

where

Using Elimination lemma [12] for

one obtains (10). If is positive definite matrix then there exists suchk that second inequality of (10) is negative definite which proves that second and third statements are equivalent. For time derivative of Lyapunov function one obtains

(13)

Due to (10) for (13)

. (14)

Equation (14) implies that closed loop system (3) with control law (2) is asymptotically stable. Furthermore, by integrating both sides of (14) from to and using state initial condition x0 one obtains

(15)

As the closed loop system is asymptotically stable if then . Hence we have obtained the condition i) of Theorem 2 which proves that all statements are equivalent.

For discrete-time system inequalities (10) and (11) read as follows

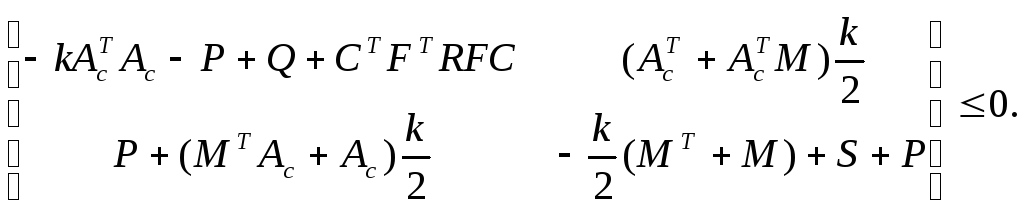. (16)

Proof of similar Theorem for discrete-time system goes the same way as for Theorem 2. Non-iterative LMI procedure to design of static output feedback is based on (11) for continuous and (16) for discrete-time systems when matrix M is . For this case the conditions “if and only if” reduces to conditions “if”. Substitute control law (2) in (11) after some manipulation the following LMI is obtained.

(17)

and . If matrix

(18)

is positive definite then inequality (17) is LMI. Similar result can be obtained for linear discrete-time systems.

R e m a r k 1 .

• Matrices R and Q can be chosen by designer. Note that obtained performance for closed loop system is determined by the ratio of matrices R and Q entries

• If for some reason (18) does not hold, in this case the linearization approach [4] may be used with respect to (8) and term

(19)

where , and second term of (17)

(20)

• Note that there exists such linear transformation to transform (1)

where for which the obtained static output feedback F (2) does not change.

For the case of (20) the LMI condition of (17) reads as follows

(21)

and where and

For the case of LMI (17) reduces to the

following LMI

4 Examples

In the first example the design techniques developed in this paper are applied to a realistic missile example [2]. In the original paper purpose is to determine the maximum admissible uncertainty level for which stability of the closed loop system with guaranteed cost is preserved. In the field of robust control example [2] serves as a benchmark example. In this paper the goal is defined as a stabilization of nominal model with static output feedback.

Table 1. The results of calculation for example 1.

Gain matrix
0.0022	-0.00918	0.0009	-1.66	-2.19	-1.85
-0.0071	0.0007	-0.0031

The dynamics of the controlled missile roll axis nominal model is described by the following matrices

The results of calculation are summarized in Table 1. , , , , , , , where , i = 1, 2, 3 is the maximum eigenvalue of the closed-loop system for the cases of (17), (19) and (21) respectively.

The second example has been borrowed from [1]. It concerns the design of static output feedback controller with a guaranteed cost for stabilizing the lateral axis nominal model dynamics for an aircraft L-1011. Let matrices A,B,C be defined