ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.05.2024
Просмотров: 71
Скачиваний: 0
Построение графиков вTurbo Pascal Общие сведения
Экран монитора делится на отдельные маленькие квадраты, которые называются пикселями. Каждый пиксель может иметь свой цвет. За счет окрашивания пикселя в различные цвета получается изображение. Положение пикселя определяется двумя координатами x и y в собственной системе координат, которую мы назовем «экранной». Начало экранной системы координат находится в левом верхнем углу экрана. Направление осей показано на рисунке.
Пиксели образуют матрицу (размер экрана) 640×480 точек (пикселей). Курсор выделяет один пиксель, но не отображается на экране. Начальное положение курсора – пиксель с координатами (0, 0).
Модуль Graph содержит описание типов, констант, процедур и функций, обеспечивающих графические возможности Turbo Pascal. Перечислим основные процедуры и функции модуля Graph.
Initgraph(var grdriver, grmode: integer; path: string) Инициализирует графический режим. Если grdriver=0, тогда драйвер выбирается по умолчанию. Grmode – значение кода этого драйвера в процедуре. Path – путь к драйверу.
Detectgraph(var graphdriver, graphmode: integer). Проверяет аппаратуру и определяет, какой графический драйвер, и в каком режиме используется.
Closegraph -Закрывает графический режим.
|
Moveto(x,y) |
курсор перемещается в координату (x,y) |
|
Lineto(x,y) |
рисует прямую от курсора до координаты (x,y) |
|
Setcolor(c) |
c – код цвета. Меняет цвет изображений. |
|
Setbkcolor(c) |
c – код цвета. Меняет цвет фона |
Здесь код цвета - выражение типа WORD, задающее текущий цвет символов или фона; в модуле GRAPH определены следующие константы для задания цвета:
|
Black |
0 |
черный |
DarcGray |
8 |
тёмно-серый |
|
Blue |
1 |
синий |
LigthBlue |
9 |
ярко-синий |
|
Green |
2 |
зеленый |
LigthGreen |
10 |
ярко-зеленый |
|
Сауп |
3 |
голубой |
LigthCyan |
11 |
ярко-голубой |
|
Red |
4 |
красный |
LigthRed |
12 |
розовый |
|
Magenta |
5 |
фиолетовый |
LigthMagenta |
13 |
малиновый |
|
Brown |
6 |
коричневый |
Yellow |
14 |
желтый |
|
LightGray |
7 |
светло-серый |
White |
15 |
белый |
Setlinestyle(x, y, z)(вид, образец, толщина) - устанавливает стиль вычерчиваемых линий.
Где x - вид - выражение типа word, означающее вид линии. Вид линии определяется следующими константами:
SolidLn = 0 ; {сплошная линия}
DottedLn = 1 ; {точечная линия}
CenterLn = 2 ; {штрих пунктирная линия}
DashedLn = 3 ; { пунктирная линия }
UserBitLn = 4 ; { вид линии определяется пользователем }
y - образец - выражение типа word, указывающее образец линии; для всех видов линий от 0 до 3 это значение задается равным нулю; для пользовательского вида задается собственный шаблон. z - толщина - выражение типа word, задающее толщину линии. Параметр толщина может принимать одно из двух значений:
NormWidth = 1 ;{толщина в одну точку}
ThickWidth = 3 ; {толщина в три точки}
Floodfill(x, y, c) – закрашивает в текущий цвет область экрана, ограниченную непрерывной линией цвета с. Текущий цвет и стиль задается с помощью SetFillStyle(p,c). (x, y) – координаты точки, начиная с которой, начинается закраска.
Setfillstyle(p,c) – задает текущий цвет и стиль. р – стиль (штриховка), с – код цвета.
Штриховка:
|
0 - фоном 1 -сплошная 2 - _ _ _ 3 - //// 4 - толстыми/// 5 - \\\\ 6 - толстыми \\\ |
7 - ++++ 8 - x x x 9- квадратами 10 - редкими точками 11 - частыми точками 12 - пользовательские
|
Arc(x, y: integer; startangle, endangle, radius: word). Рисует дугу от начального угла к конечному, (x, y) — центр.
Bar(x1, y1, x2, y2: integer). Рисует прямоугольник, используя текущий стиль и цвет.
Bar3d(x1,y1,x2,y2: integer; depth: word; top: boolean). Рисует параллелепипед, используя текущий стиль и цвет.
Circle(x, y: integer; radius: word) Рисует окружность, (x, y) — центр.
Cleardevice Очищает графический экран, устанавливая текущей точку (0,0).
Ellipse(x, y: integer; startangle, endangle, xradius, yrRadius : word). Рисует эллиптическую дугу от начального угла к конечному, (x, y) — центр.
Line(x1, y1, x2, y2: integer). Рисует прямую линию от точки (x1, y1) до точки (x2, y2).
Outtextxy(x, y: integer; textstring: string). Выводит текст на экран, начиная с точки (x, y).
Putpixel(x, y: integer; colorpixel: word). Высвечивает на экране точку (пиксель) с координатами (x, y) цветом colorpixel.
Rectangle(x1, y1, x2, y2: integer) Рисует рамку текущим цветом и типом линий.
Getmaxx: integer Возвращает максимальную горизонтальную координату x.
Getmaxy: integer Возвращает максимальную вертикальную координату y.
Построение графика
Требуется составить программу построения на экране дисплея графика функции y = F(x).
Решение этой задачи удобно проводить в следующем порядке:
Определим границы значений аргумента в декартовых координатах, в пределах которых будет строиться график X
 [Xmin,
Xmax].
[Xmin,
Xmax].
Для данной области значений аргумента определим предельные значения функции: Y
 [Ymin,
Ymax].
Эти значения необязательно должны
быть точными. Они могут быть оценочными
снизу и сверху соответственно.
[Ymin,
Ymax].
Эти значения необязательно должны
быть точными. Они могут быть оценочными
снизу и сверху соответственно.Зададим границы графического окна в графических координатах, в пределах которого будет рисоваться график: [Xgmin, Xgmax] – по горизонтали, [Ygmin, Ygmax] – по вертикали.
Учесть, что Ygmin > Ygmax, поскольку в графических координатах вертикальная ось направлена вниз.
Таким образом, имеем две системы координат [x, y] – математическая или декартова система координат и [xg, yg] – экранная система координат.
Получим формулы связи между этими системами.
Нетрудно получить формулу, связывающую экранные и математические координаты:
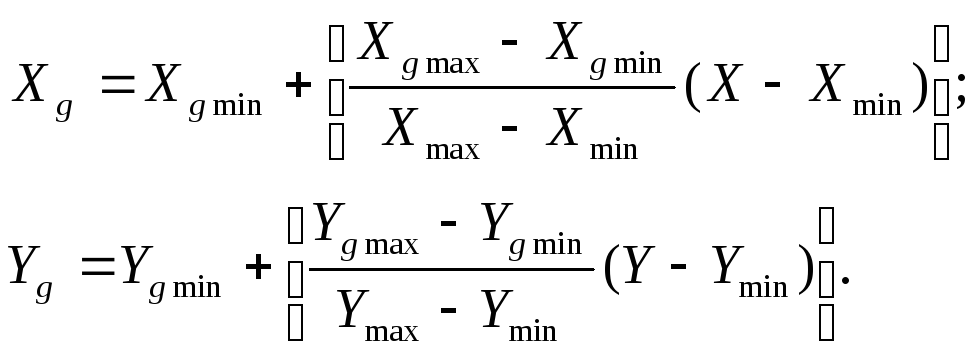 (*)
(*)
Здесь квадратные скобки означают округление до целого значения (функция Round).
Построение графика функции может производиться либо точечным методом, либо кусочно-линейным. При первом способе график строится как последовательность точек, расположенных максимально близко. Производится «попикселевый» перебор значений аргумента xg в интервале [Xgmin , Xgmax] с выставлением точек с соответствующими координатами Yg.
При кусочно-линейном методе задается шаг ΔX и рассчитывается последовательность значений (Xi , Yi):
![]()
Данный расчет производится в декартовой системе координат.
График строится в виде отрезков прямых, проведенных через точки (Хi, Yi), (Xi+1, Уi+1).
Точечный метод построения графика
Составим программу
построения графика функции у
= cos(x)
для х![]() [0; 2π], используя
точечный метод.
[0; 2π], используя
точечный метод.
Из условия задачи следует, что Xmin = 0, Хтax= 2π. В этих пределах функция cos х меняется от -1 до 1. Поэтому Ymin = -1, Ymax = 1.
Выберем следующие границы графического окна:
Xgmin=10; Xgmax=400; Ygmin= 300; Ygmax=40.
График строится в виде последовательности точек с математическими координатами
Xi = Xmin + i ∙ h; Yi =cos(Xi); i = 0, ...,390.
Шаг h выбирается минимально возможным, соответствующим шагу графической сетки:
![]()
Приведенные выше формулы перевода декартовых координат в экранные примут вид:
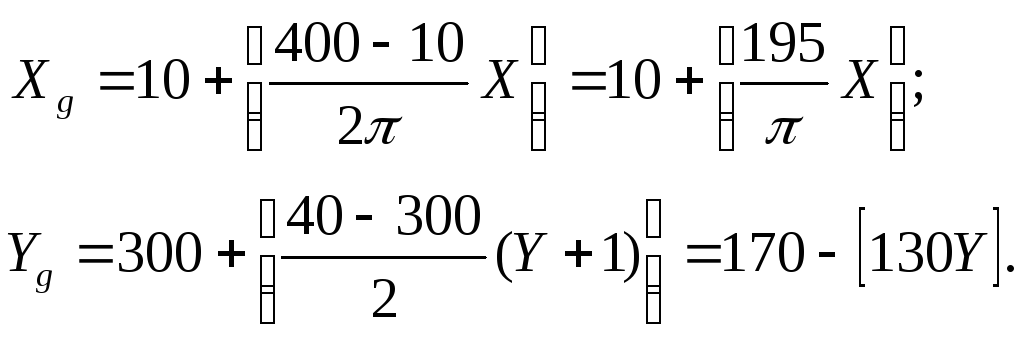
Вместе с графиком функции строятся оси координат. Строить их будем с помощью команды рисования линии line. Ось X имеет координату Yg= 170, ось Y — координату Xg = 10.
Uses Graph;
Var Driver,Mode: Integer;
X: Real; Xg,Yg,I: Integer;
Begin {Инициализация графического режима}
Driver:=Detect;
InitGraph(Driver,Mode,'C:\TP\BGI');
SetColor(White);{белый цвет линий}
SetBkColor(DarcGray);{задан темно-серый цвет фона}
Line(10,170,400,170); {строит ось X}
Line(10,20,10,320); {строит ось Y}
{Построение графика функции желтыми точками}
x:=0;
For I:=0 To 390 Do
Begin
Xg:=10+Round(195/(Pi)*(X));
Yg:=170-Round(130*cos(X));
PutPixel(Xg,Yg,Yellow);
X:=X+Pi/195
End;
{Разметка осей, запись функции}
OutTextXY(15,30,'Y');
OutTextXY(405,170,'X');
OutTextXY(190,40,'Y=COS(X)');
ReadLn; {задержка экрана}
CloseGraph; {выход из графики}
End.
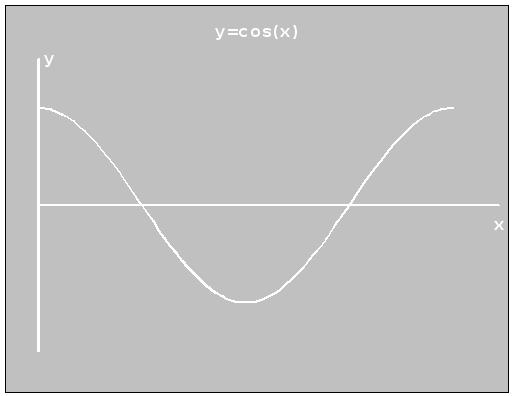
Рисунок 1