Файл: Lab_1_1_marina.docx

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования  "Ковровская государственная технологическая академия имени В.А.Дегтярева"

Кафедра физики

ОТЧЁТ

по лабораторному практикуму дисциплины

«ФИЗИКА»

Руководитель: Кузнецов Н.А.

Исполнил: ст. гр. ВП-112

Хименкова М.А.

Ковров 2013

Лабораторная работа № 1.1

Определение объема цилиндра

Цель работы: научиться производить измерения с помощью штангенциркуля и микрометра, а также освоить способы обработки результатов измерений.

Задание к работе:

К работе допущен:

Работу выполнил:

Работу защитил:

Введение

При выполнении лабораторных работ студент должен овладеть мето­дами измерения физических величин и математической обработки результа­тов измерений.

Измерение физической величины заключается в сравнении ее с другой однородной физической величиной, принятой за единицу. Различают два вида измерений: прямые и косвенные.

1. Прямые измерения - это такие измерения, когда искомая величина определяется непосредственно с помощью инструмента или прибора, шкала которого проградуирована в единицах измерения определяемой величины. Прямые измерения бывают двух типов:

а) прямые единичные (однократные) измерения - это такие измерения, при которых их повторение дает один и тот же результат или, по условиям опыта, повторить измерение невозможно;

б) прямые многократные измерения — это такие измерения, при кото­рых их повторение дает разные результаты. Число повторных измерений и называется выборкой.

2. Косвенные измерения — это такие измерения, когда искомая величи­на вычисляется по данным прямых измерений по соответствующим функ­циональным зависимостям, устанавливающим связь между искомой величи­ной и этими прямыми измерениями.

---

Измерить абсолютно точно принципиально невозможно по следую­щим причинам:

а) невозможно изготовить абсолютно точный прибор в связи с по­грешностями изготовления;

б) приборы изнашиваются, стареют, в результате чего их точность уменьшается;

в) силы взаимодействия (силы трения, тяжести и т.д.) и внешние фак­торы (температура окружающей среды, давление, влажность, электрические и магнитные поля) изменяют измеряемые параметры тол, сред и влияют ни характеристики прибором;

г) измеряемые параметры часто изменяются н пространстве и во вре­мени. Например, диаметр проволоки или температура помещения;

д) точность измерения зависит от квалификации экспериментатора.

Влияние этих факторов приводит к возникновению погрешностей из­мерений. Все погрешности делятся на две группы:

а) систематические погрешности - это такие погрешности, когда при повторении измерений величина и знак погрешности остаются неизменны­ми. Например, часы каждые сутки «уходят вперед» на 10 секунд^-

б) случайные погрешности - это такие погрешности, когда при повто­рении измерений величина и знак погрешности изменяются хаотически. Случайные погрешности возникают вследствие неоднозначности измеряе­мых параметров в пространстве и времени, а также влияния внешних факто­ров. Например, диаметр проволоки случайно изменяется по ее длине в обе стороны относительно среднего значения.

Для оценки точности выполненных измерений рассчитываются абсо­лютная и относительная погрешности.

Абсолютной погрешностью измерения ∆х_и называется разница между истинным и измеренным значениями искомой величины, измеряемая в тех же единицах, что и измеряемая величина:

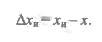
Однако абсолютная погрешность недостаточно полно характеризует точность измерения. Если расстояние между городами и длину карандаша измерить одним и тем же прибором, то точность измерений в первом случае будет намного выше. В связи с этим вводится понятие относительной по­грешности.

Относительной погрешностью называется отношение абсолютной по­грешности к измеренной величине, измеряется в процентах:

---

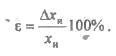
Так как истинное значение физической величины определить невоз­можно, то за результат измерений принимается действительное значение физической величины х_а, которое определяется тем или иным способом в зависимости от вида измерений и объёма выборки. Действительное значение физической величины будет сколь угодно близко приближаться к истинному значению только при бесконечно большой выборке (п —►∞). Поскольку практически выборки содержат конечное (и, как правило, небольшое число измерений п) между действительным и истинным значениями существует различие, определить которое невозможно. Однако возможно определить интервал значений измеряемой величины х_д ± ∆х, называемый доверитель­ным интервалом, в который истинное значение измеряемой величины попа­дав! с известной вероятностью а, называемой надежностью доверительно­го интервала. Величина ∆х называется границей доверительного интервала.

Определение погрешностей прямых единичных измерений

1. За действительное значение принимается измеренное значение фи­зической величины:

x_д=х.

2) В качестве границ доверительного интервала принимается абсолют­ная погрешность, которая вычисляется:

а) по классу точности прибора. Класс точности к является технической характеристикой прибора и указывается на панели прибора или в его техни­ческом паспорте: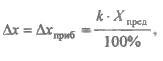

где - предел измерения прибора, т.е. наибольшая величина, которую прибор способен измерить;

б) по цене деления прибора. Если у прибора не указан класс точности (например, линейка, термометр), то в качестве абсолютной погрешности берут иену деления прибора.

3) Относительная погрешность определяется по формуле: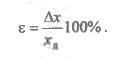

4) Надежность доверительного интервала принимаем равной единице:

а = 1

5. Окончательный ответ записывается в виде: х = (х_д± ∆х) единицы измерения с ɛ% (α = 1).

Определение погрешностей прямых многократных измерений

1. За действительное значение принимается среднее значение физиче­ской величины:

---

x_я=x

Пусть неизвестную величину измерили n раз:

Тогда среднее значение определяется по формуле:

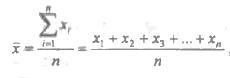
где n - число измерений.

2. Определяют абсолютную погрешность каждого измерения:

3. Вычисляют среднеквадратичную погрешность среднего арифметического значения (стандарт):

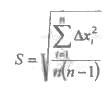
4. Надежность доверительного интервала принимаем равной 0,9. По числу измерений и надежности определяют коэффициент Стьюдента t_a(n).

Число измерений	2	3	4	5	6	7	8	9	10	ОС
Коэффициент Стьюдента	6,3	2,9	2,4	2.1.	2,0	1,9	1,9	1,9	1,8	1,6

5. Вычисляют случайную ошибку измерений:

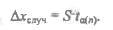
6. Определяют приборную ошибку (см. первый способ п.2 (а,б)).

7. Вычисляют абсолютную суммарную погрешность по формуле:

которую принимают за границу доверительного интервала.

8. Относительная погрешность определяется по формуле:

---

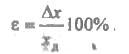
9. Окончательный ответ записывается в виде: x = (x_д ± ∆х) единицы измерения с ɛ % (α = 0,9).

Определение погрешностей косвенных измерений

Погрешность косвенного измерения складывается из погрешностей прямых измерений. Определение погрешностей косвенных измерений мож­но проводить двумя способами.

Первый способ.

1. За действительное значение принимается рассчитанное по формуле значение физической величины:

где a_д,b_д - действительные значения прямых измерений.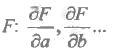

2. Вычисляют частные производные функции г:

3. Вычисляют абсолютные погрешности прямых измерений, входящих в исходную функцию F: ∆а, ∆b...

Если в расчетной формуле для х_а используется величина, взятая из таблицы, или округленная математическая константа, то при расчете ∆х сле­дует учитывать погрешность табличной величины. За погрешность табличной величины принимают половину разряда последней значащей цифры числа.

Например:

Табличное значение величины	Разряд последней значащей цифры	Погрешность табличной величины
π = 3,14	0,01	∆x = ∆х табл = ∆π = 0,005
ρ = 9860 кг*м-3	1	∆x = ∆х табл = ∆ρ= 0,5 кг-м'3
R3 = 6,4*106 м	0,1*106	∆x = ∆х табл = ∆R3 = 0,05 106м

4. Гринины доверительного интервала косвенного измерения вычис­ляют по соотношению:

---