Файл: Электричество и магнетизм.doc

10. Законы Кирхгофа

Значения токов и напряжений для сложных разветвленных цепей можно находить при помощи законов Кирхгофа.

П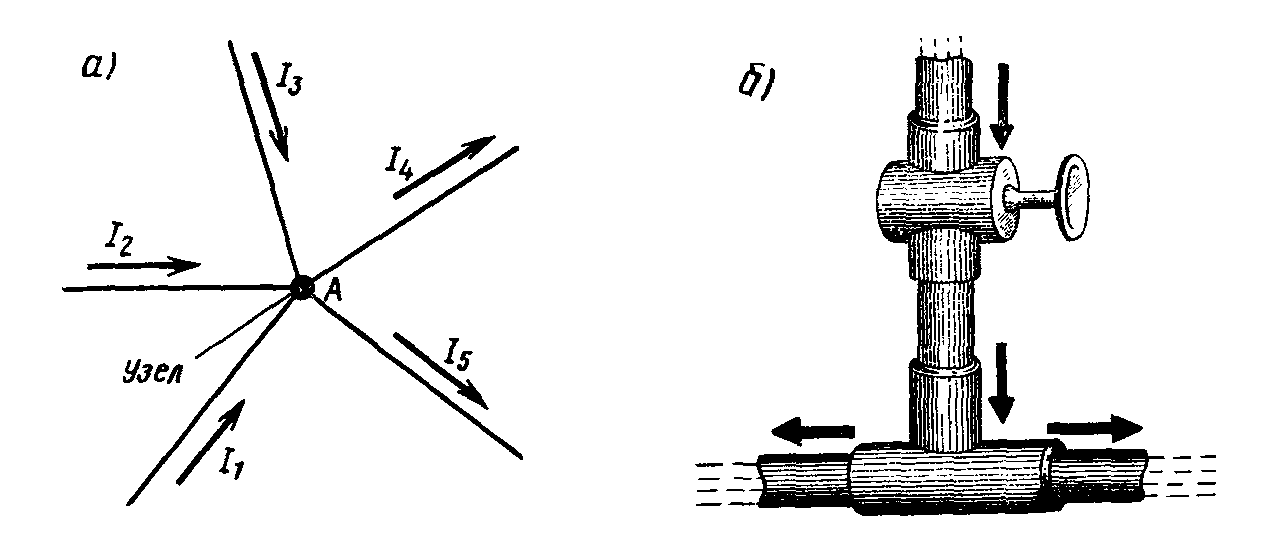ервый закон Кирхгофа устанавливает зависимость между токами для узлов электрической цепи, к которым подходит несколько ветвей. Согласно этому закону алгебраическая сумма токов ветвей, сходящихся в узле электрической цепи, равна нулю:

ΣI=0

При этом токи, направленные к узлу, берут с одним знаком (например, положительным), а токи, направленные от узла, - с про-тивоположным знаком (отрицатель-ным). Например, для узла А (рис. 17,а)

I₁ + I₂+ I₃- I₄- I ₅ = 0

Преобразуя это уравнение, получим, что сумма токов, направленных к узлу электрической цепи, равна сумме токов, направленных от этого узла:

I₁ + I₂+ I₃= I₄+ I ₅

Второй закон Кирхгофа устанавливает зависимость между э. д. с. и напряжением в замкнутой электрической цепи. Согласно этому закону во всяком замкнутом контуре алгебраическая сумма э. д. с. равна алгебраической сумме падений напряжения на сопротивлениях, входящих в этот контур:

ΣE = Σ IR

При составлении формул, характеризующих второй закон Кирхгофа, значения э. д. с. E и падений напряжений IR считают положительными, если направления э. д. с. и токов на соответствующих участках контура совпадают с произвольно выбранным направлением обхода контура. Если же направления э. д. с. и токов на соответствующих участках контура противоположны выбранному направлению обхода, то такие э. д. с. и падения напряжения считают отрицательными.

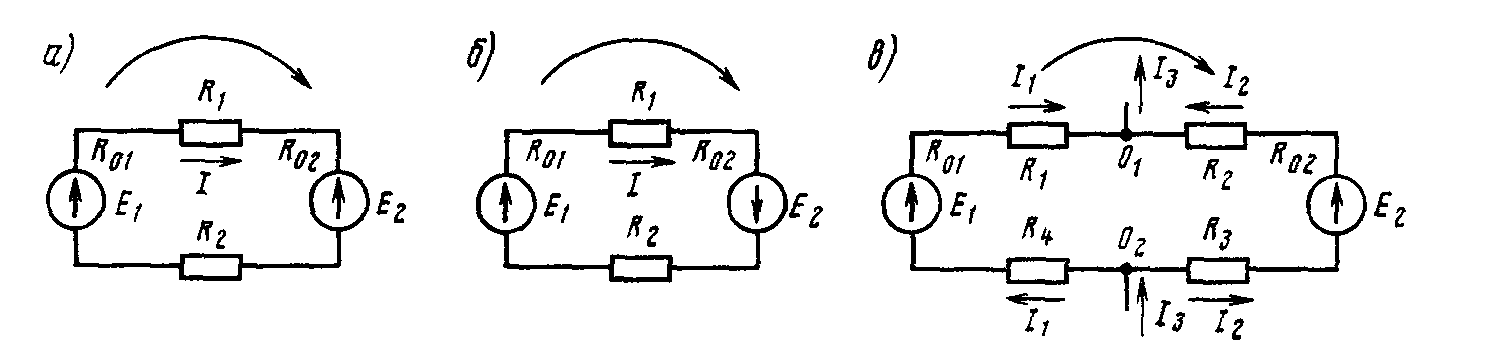
Рассмотрим в качестве примера электрическую цепь, в которой имеются два источника с электродвижущими силами Е₁ и Е₂ (рис. 18,а), внутренними

сопротивлениями и два приемника с сопротивлениями R₁ и R₂. Применяя второй закон Кирхгофа для этой цепи и выбирая направление ее обхода по часовой стрелке, получим:

Е₁ - Е₂ = IR₀₁ + IR₀₂ + IR₁ + IR₂

При этом э. д. с. E₁ и ток I совпадают с выбранным направлением обхода контура и считаются положительными, а э. д. с. Е₂, противоположная этому направлению, считается отрицательной.

Если в электрической цепи э. д. с. источников электрической энергии при обходе соответствующего контура направлены навстречу друг другу (см. рис. 18, а), то такое включение называют встречным. В этом случае на основании второго закона Кирхгофа ток

I = (Е₁ - Е₂)/( R₁ + R₂ + R₀₁+R₀₂).

Если же э. д. с. источников электрической энергии имеют по контуру одинаковое направление (рис. 24, б), то такое включение называют согласным и ток

I = (Е₁ +Е₂)/( R₁ + R₂ + R₀₁+R₀₂)

В некоторых случаях такое включение недопустимо, так как ток в цепи резко возрастает.

Если в электрической цепи имеются ответвления (рис. 18,в), то по отдельным ее участкам проходят различные токи I₁ и I₂. Согласно второму закону Кирхгофа

(Е₁ - Е₂) = I₁R₀₁ + I₁R₁ - I₂R₂ -I₂R₀₂ - I₂R₃+ I₁R₄

При составлении этого уравнения э. д. с. Е₁ и ток I₁ считаются положительными, так как совпадают с принятым направлением обхода контура, э. д. с. Е₂ и ток I₂— отрицательными.

11. Последовательное, параллельное и смешанное соединения резисторов.

Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление. Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов (приемников электрической энергии): последовательное, параллельное и смешанное.

Последовательное соединение. При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго, конец второго - с

началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит один и тот же ток I.

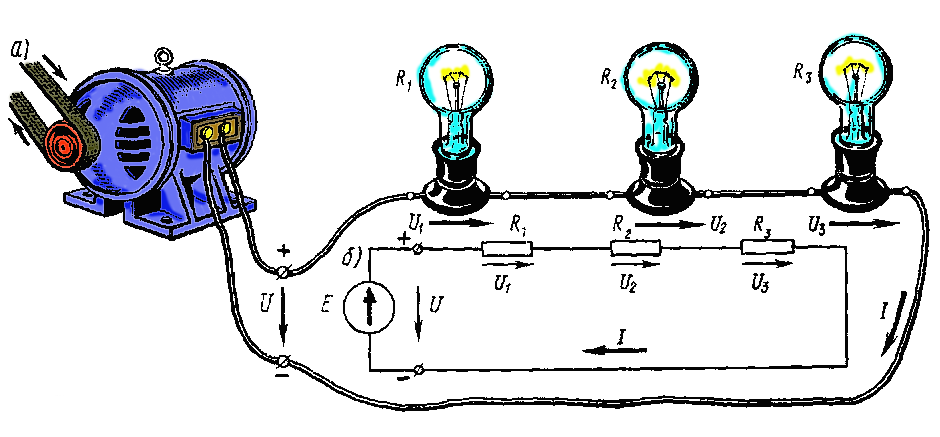
Последовательное соединение приемников поясняет рис. 19,а. Заменяя лампы резисторами с сопротивлениямиR₁, R₂ и R₃ получим схему, показанную на рис. 19,б.Если принять, что в источнике R₀ = 0, то для трех последова-тельно соединенных резисторов согласно второму Кирхгофа можно написать:

E = IR₁ +IR₂ +IR₃ = I( R₁+ R₂+ R₃ ) = IR_общ ;

где: R_общ = R₁+ R₂+ R₃

Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов.

Напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.

Соединять последовательно целесообразно только приемники с одинаковыми сопротивлениями. В противном случае приложенное напряжение источника электрической энергии распределяется между ними неравномерно и отдельные приемники могут оказаться под недопустимо высоким для них напряжением.

При последовательном соединении приемников изменение сопротивления одного из них влечет за собой изменение напряжения на других связанных с ним приемниках. При обрыве электрической цепи в одном из приемников в остальных прекращается ток.

П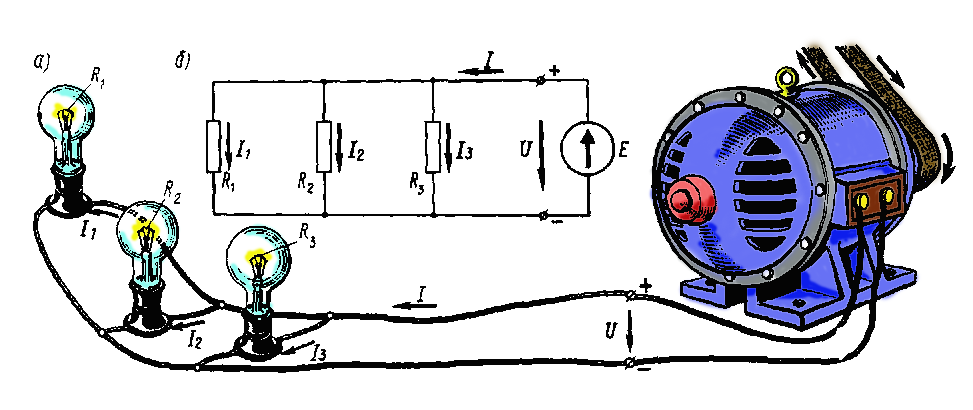ри параллельном соединении приемники включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 20,а). Заменяя лампы резисторами с сопро-тивлениями R₁, R₂ и R₃, получим схему, показанную на рис. 20,б.

При параллельном соединении ко всем резисторам приложено одинаковое напряжениеU. Поэтому согласно закону Ома:

I₁ = U/R₁, I₂ =U/R₂ , I₃ = U/R₃

Ток в неразветвленной части цепи согласно первому закону Кирхгофа I=I₁+I₂ +I₃ или

I= U/R₁ + U/R₂ + U/R₃ = U (1/ R₁ + 1/ R₂+ 1/ R₃) = U/R_экв

Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой

1/ R_экв= 1/ R₁ + 1/ R₂+ 1/ R₃

При увеличении числа параллельно включаемых резисторов результирующее сопротивление уменьшается.

При параллельном соединении приемников все они находятся под одним и тем же напряжением и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными.

С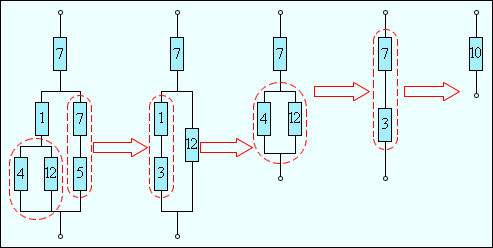мешанным соединением называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом