Добавлен: 29.10.2018
Просмотров: 492
Скачиваний: 10
СОДЕРЖАНИЕ
Использование гистограмм для отображения характера распределения случайной величины
Алгоритм построения гистограммы:
Генератор дискретно-распределенных значений:
Генерация дискретных распределений с заданным характером распределения вероятностей
Генерация непрерывных распределений вещественных величин
Использование гистограмм для отображения характера распределения случайной величины
Пусть имеется генератор случайных чисел в диапазоне от a до b. Для простоты пусть это будет генератор равномерно распределенных числовых значений. Такое распределение можно получить, например, следующей языковой конструкцией VFP:
x = a + (b-a)*rand().
Гистограмма представляет собой множество узких, одинаковой ширины и равноудаленных друг от друга, вертикальных прямоугольников. Количество прямоугольников гистограммы соответствует количеству отрезков, на которые разбивается отрезок (a,b), высота прямоугольников соответствует количеству случайных значений попавших в данный отрезок.
Алгоритм построения гистограммы:
A = левая граница
B = правая граница
N = кол-во разбиений
M = кол-во испытаний
Массив AN(N)
** AN(i) элемент массива – соответствует количеству попаданий в i-ый элементарный
** отрезок
H = (B-A)/N && ширина элементарного отрезка
Цикл по L от 1 до N
AN(L)=0
КонецЦикла
Цикл по k от 1 до M && цикл ипытаний
X = ГенераторСлучайнойВеличины(a,b)
Цикл по L от 1 до N
LB = A + (L-1)*H && левая граница элементарного отрезка
RB = LB + H
Если x>=LB и x< RB тогда
AN(L) = AN(L) + 1
Выход из цикла
КонецЕсли
КонецЦикла
КонецЦикла
Цикл по L от 1 до N
ОтрисовкаСтолбца(L, AN(L))
КонецЦикла
Функция ГенераторСлучайнойВеличины
Параметры a,b
Возврат a + (b-a)*rand()
* Здесь rand() – системная функция возвращающая
* равномерно-распределенное случайное число от 0 до 1.
КонецФункции
Функция ОтрисовкаСтолбца
Параметры NS, HS
** NS – номер столбца
** HS – высота столбца
** ЛевоеПоле = значение левого поля в точках
** ШиринаСтолбца = Значение ширины столбца в точках
** Зазор = Значение зазора между столбцами в точках
x1= ЛевоеПоле + (ШиринаСтолбца + Зазор) * (NS-1)
** вычисляем левую границу столбца NS
x2 = x1 + ШиринаСтолбца
Отрисовка столбца номер NS и высоты HS
КонецФункции
Приведенный алгоритм построения гистограммы можно оптимизировать. Вместо цикла:
X = ГенераторСлучайнойВеличины(a,b)
Цикл по L от 1 до N
LB = A + (L-1)*H && левая граница элементарного отрезка
RB = LB + H
Если x>=LB и x< RB тогда
AN(L) = AN(L) + 1
Выход из цикла
КонецЕсли
КонецЦикла
в котором определяется номер диапазона можно использовать более простой способ: L = ОкруглитьВверх((x-A)/h)
Для построения гистограммы из N столбцов по результатам M испытаний генератора случайных чисел в диапазоне от A до B можно использовать следующий фрагмент программы на VFP:
h=(B-A)/N
For k = 1 to M && цикл ипытаний
X = ГенераторСлучайнойВеличины()
L=ceiling((x-a)/h)
IF L>=1 AND L<=N
AN(L)=AN(L)+1
ELSE
IF L=0
AN(1)=AN(1)+1
ELSE
? x,L
ENDIF
ENDIF
EndFor
Генератор дискретно-распределенных значений:
Построим генератор дискретных случайных величин с заданными вероятностями на основе системного генератора равномерно-распределенной величины от 0 до 1: Пусть величина xi может принимать N-значений с вероятностями pi:
|
Xi |
Pi |
|
1 |
0.1 |
|
2 |
0.2 |
|
3 |
0.3 |
|
4 |
0.1 |
|
5 |
0.2 |
|
6 |
0.1 |
Алгоритм основывается на свойстве равномерного распределения равномерно заполнять отрезок от 0 до 1, причем вероятность попадания случайного значения в подинтервал отрезка (0,1) шириной D равна ширине этого подинтервала. Например, если отрезок (0,1) разбить на два подинтервала (0,0.2) и (0.2, 1), то вероятность попадания в подинтервал (0? 0.2) будет равна 0.2, а вероятность попадания в отрезок (0.2, 1) будет равна 0.8. Таким образом, для вышеприведенной таблицы необходимо разбить отрезок (0,1) на 6 подинтервалов.
|
Xi |
Pi |
Wi Ширина |
LBi Левая граница |
RBi Правая граница |
|
1 |
0.1 |
0.1 |
0 |
0.1 |
|
2 |
0.2 |
0.2 |
0.1 |
0.3 |
|
3 |
0.3 |
0.3 |
0.3 |
0.6 |
|
4 |
0.1 |
0.1 |
0.6 |
0.7 |
|
5 |
0.2 |
0.2 |
0.7 |
0.9 |
|
6 |
0.1 |
0.1 |
0.9 |
1 |
LB(1)=0, RB(1) = LB(1) + P(1)
Остальные элементы массивов левых и правых границ можно вычислить в цикле
Цикл по I от 2 до N
LB(i) = LB(i-1) + W(i-1)
RB(i) = LB(i) + P(i)
КонецЦикла
Первый вариант алгоритма
Функция ГенераторДискретныхЗначений
N=6
Массив P(N), LB(N), RB(N),W(N)
СчитываемМассив(@P,N)
LB(1)=0
RB(1) = LB(1) + P(1)
Цикл по I от 2 до N
LB(i) = LB(i-1) + W(i-1)
RB(i) = LB(i) + P(i)
КонецЦикла
XR = rand()
LB = 0
Если XR>=LB(1) и XR<RB(1)
Возврат X(1)
ИначеЕсли XR >=LB(2) и XR <RB(2)
Возврат X(2)
ИначеЕсли XR >=LB(3) и XR <RB(3)
Возврат X(3)
ИначеЕсли XR >=LB(4) и XR <RB(4)
Возврат X(4)
ИначеЕсли XR >=LB(5) и XR <RB(5)
Возврат X(5)
ИначеЕсли XR >=LB(6) и XR <=RB(6)
Возврат X(6)
КонецЕсли
КонецФункции
Функция ГенераторДискретныхЗначений
N=6
Массив P(N), X(N)
XR = rand()
LB = 0
Цикл по i=1 до N
Если xr>=LB и xr<LB+P(i)
Возврат X(i)
КонецЕсли
LB = LB + P(i)
КонецЕсли
Возврат 0
КонецФункции
Генерация дискретных распределений с заданным характером распределения вероятностей
Рассмотрим ситуацию, когда известны не вероятности событий Xi, а количества их реализации или другие величины пропорциональные вероятностям Pi.
Пусть необходимо построить генератор дискретных величин X(1), X(2), … X(N), N=10, вероятности реализации которых, пропорциональны величинам PR(1), PR(2), … PR(N).
Для реализации такого алгоритма необходимо найти вероятности P(i) реализации i-ой величины X(i). Затем, на основе массива P(i) рассчитать левые LB(i), правые RB(i) границы i-ых подинтервалов на отрезке (0,1). Можно не вычислять массив RB(i), поскольку RB(i) = LB(i)+P(i)
|
X(i) |
PR(i) |
P(i) |
LB(i) |
RB(i) |
|
1 |
10 |
|
0 |
|
|
2 |
32 |
|
|
|
|
3 |
120 |
|
|
|
|
4 |
220 |
|
|
|
|
5 |
100 |
|
|
|
|
6 |
56 |
|
|
|
|
7 |
45 |
|
|
|
|
8 |
30 |
|
|
|
|
9 |
70 |
|
|
|
|
10 |
120 |
|
|
|
Найдем массив вероятностей P(i). Найдем сумму всех PR(i):
![]()
Тогда массив вероятностей P(i) = PR(i)/S.
Левая граница первого отрезка должна быть равна нулю: LB(1) =0, соответственно правую границу первого отрезка находим как:
RB(1)= LB(1)+P(1)
Остальные элементы массивов LB(i) и RB(i) можно определить в цикле:
Цикл по i=2 до N
LB(i) =LB(i-1)
RB(i) = LB(i)+P(i)
Конец Цикла
Xr = rnd
Цикл по i=1 до N
Если xr>= LB(i) и xr < RB(i) тогда
Возврат X(i)
Конец Если
Конец Цикла
Генерация непрерывных распределений вещественных величин
Псевдо нормальное распределение
Рассмотрим очень простой метод генерации колоколообразного распределения вещественной величины. Этот метод основан на следующем факте: если сложить результаты N независимых экспериментов возвращающих равномерно распределенные случайные величины от о до 1, тогда вероятность получения близких к нулю величин и близких к N будет низка, а вероятность получения значений близких к N/2 – велика. Само распределение будет иметь вид колокола и если N устремить к бесконечности, тогда получится так называемое «Нормальное» распределение.
Функция ГенераторПсевдоНормальногоРаспределения
n=10
x=0
Цикл по I от 1 до n
x=x+RAND()
КонецЦикла
Возврат x/10
КонецФункции
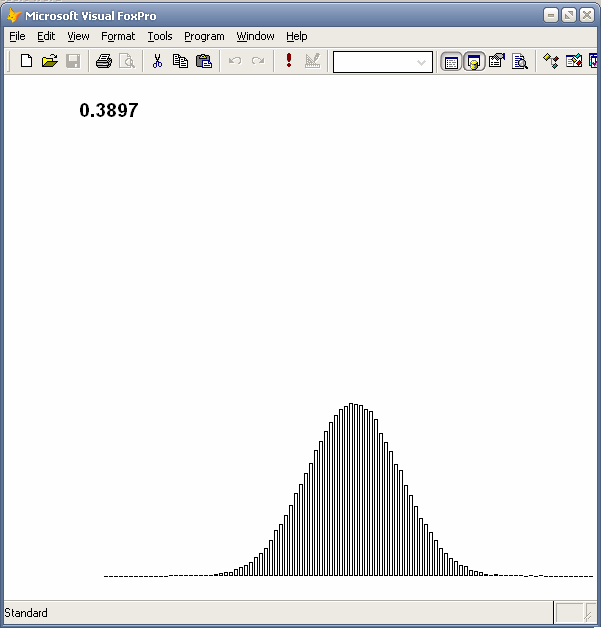
Вид гистограммы нормального распределения. Количество испытаний 100000, интервалов – 100.
Генерация линейно возрастающего распределения
Распределение непрерывной вещественной величины с вероятностью линейно-возрастающей от 0 до 1 дает следующий, очень простой алгоритм
Функция ГенераторЛинейноВозрастающегоРаспределения
x=RAND()
Возврат x^0.5
КонецФункции
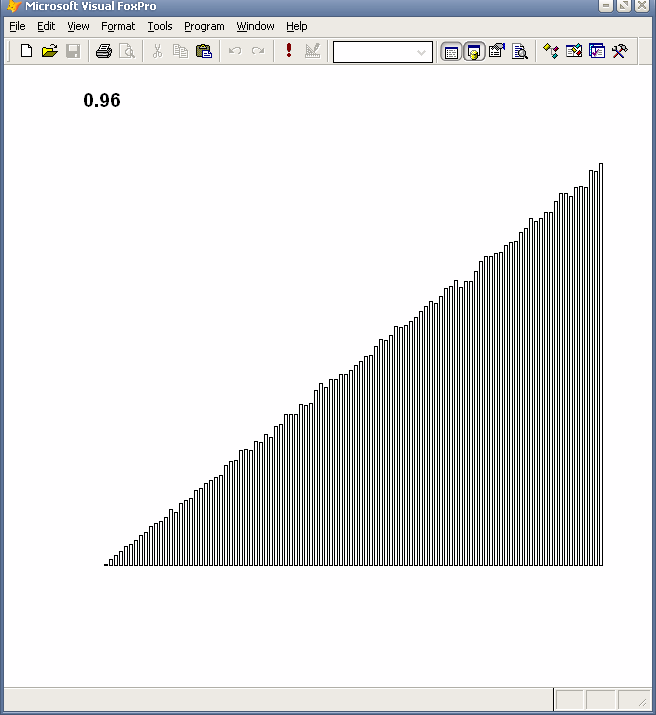
Гистограмма результатов 400000 испытаний линейно-возрастающего генератора непрерывных случайных величин от 0 до 1 (количество разбиений интервала (0,1) - 100)
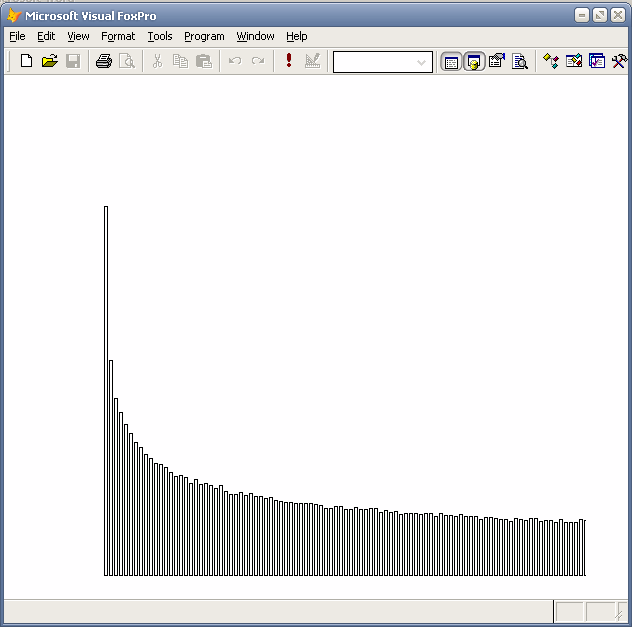
Гистограмма распределения x^1.5
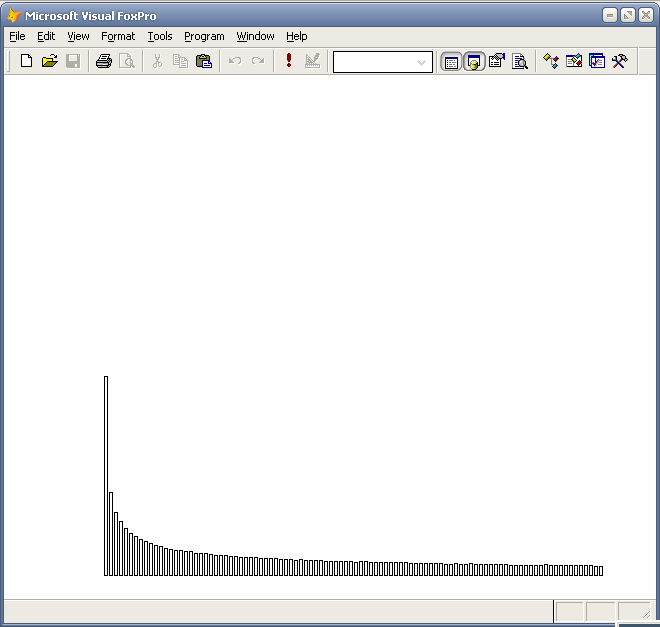
Гистограмма распределения x^2
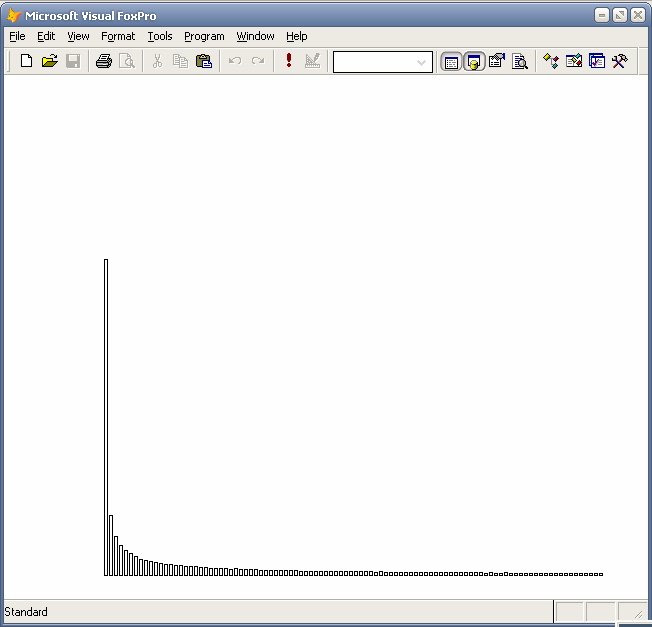
Гистограмма распределения x^4
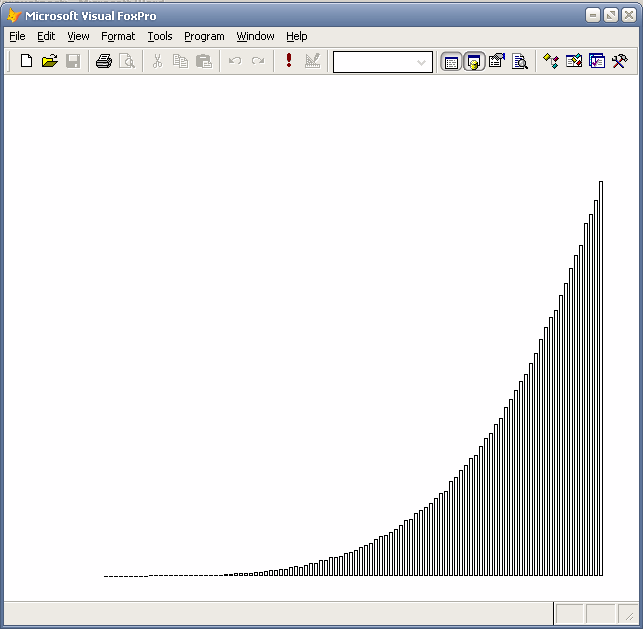
Гистограмма распределения x^0.2
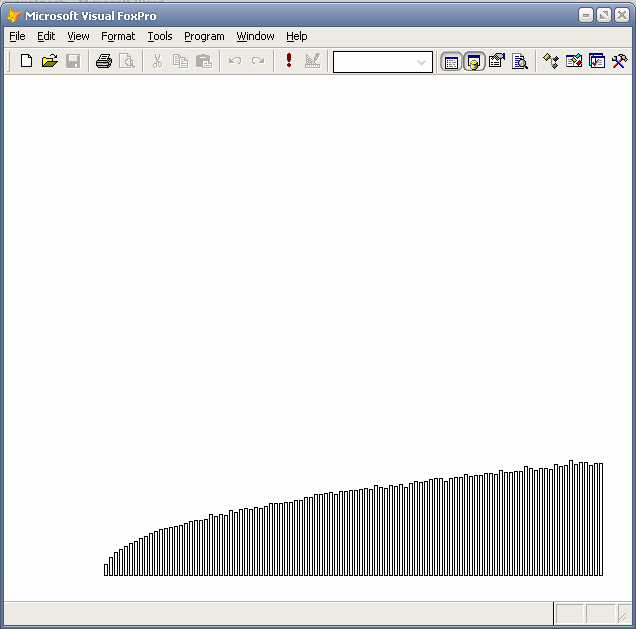
Гистограмма распределения x^0.7
Комбинированные распределения
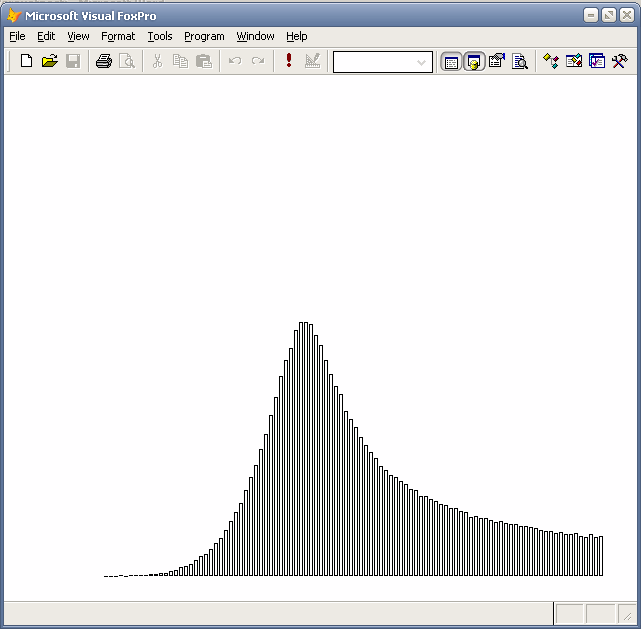
Гистограмма распределения (x^0.2 + x^4)/2