Построение сетевых моделей

Важнейшими этапами сетевого планирования являются следующие:

1. расчленение комплекса работ на отдельные части и их закрепление за ответственными исполнителями;

2. выявление и описание каждым исполнителем всех событий и работ, необходимых для достижения поставленной цели;

3. построение первичных сетевых графиков и уточнение содержания планируемых работ;

4. сшивание частных сетей и построение сводного сетевого графика выполнения комплекса работ;

5. обоснование или уточнение времени выполнения каждой работы в сетевом графике.

При построении сетевого графика необходимо соблюдать ряд правил.

1. В сетевой модели не должно быть "тупиковых" событий, т.е. событий, из которых не выходит ни одна работа, за исключением завершающего события.

2. В сетевом графике не должно быть "хвостовых" событий (кроме исходного), которым не предшествует хотя бы одна работа-событие

3. В сети не должно быть замкнутых контуров и петель, т.е. путей, соединяющих некоторые события с ними же самими.

4. Любые два события должны быть непосредственно связаны не более чем одной работой стрелкой.

5. В сети рекомендуется иметь одно исходное событие и одно завершающее событие.

Фиктивные работы и события необходимо вводить и в ряде других случаев. Один из них - отражение зависимости событий, не связанных с реальными работами. Другой случай - неполная зависимость работ.

Важным элементом построения сетевой модели является упорядочение сетевого графика. Упорядочение сетевого графика заключается в таком расположении событий и работ, при котором для любой работы предшествующее ей событие расположено левее и имеет меньший номер по сравнению с завершающим эту работу событием. Другими словами в упорядоченном сетевом графике все работы-стрелки направлены слева направо: от событий с меньшими номерами к событиям с большими номерами.

Расчет плановых параметров сетевых графиков

Временные параметры сетевых графиков приведены в следующей таблице.

Элемент сети, характеризуемый параметром	Наименование параметра	Условное обозначение параметра
Событие i	Ранний срок свершения события Поздний срок свершения события Резерв времени события	tР(i) tП(i) R(i)
Работа j	Продолжительность работы Ранний срок начала работы Ранний срок окончания работы Поздний срок начала работы Поздний срок окончания работы Полный резерв времени работы Частный резерв времени работы первого вида Частный резерв времени работы второго вида или свободный резерв времени работы Независимый резерв времени работы	t(i; j) tрн(i; j) tро(i; j) tпн(i; j) tпо(i; j) RП(i; j) R1(i; j) RС(i; j) Rн(i; j)
Путь L	Продолжительность пути Продолжительность критического пути Резерв времени пути	t(L) tКР К(L)

---

Рассмотрим содержание и расчет указанных в таблице параметров.

Начнем с параметров событий.

Как уже отмечалось, событие не может наступить прежде, чем совершаться все предшествующие работы. Поэтому ранний (или ожидаемый) срок t_p(i) свершения i-го события определяется продолжительностью максимального пути, предшествующего этому событию:

,

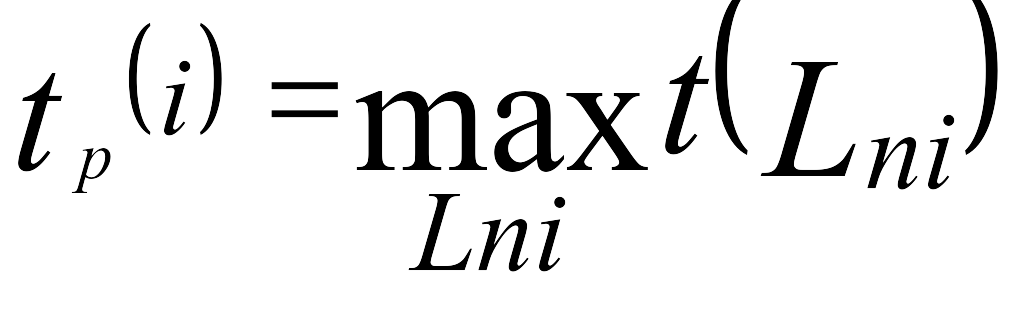где L_ni - любой путь, предшествующий i-му событию, т.е. от исходного до i-го события сети.

Если событие j имеет несколько предшествующих путей, а, следовательно, несколько предшествующих событий i, то ранний срок свершения события j находится по формуле:

.

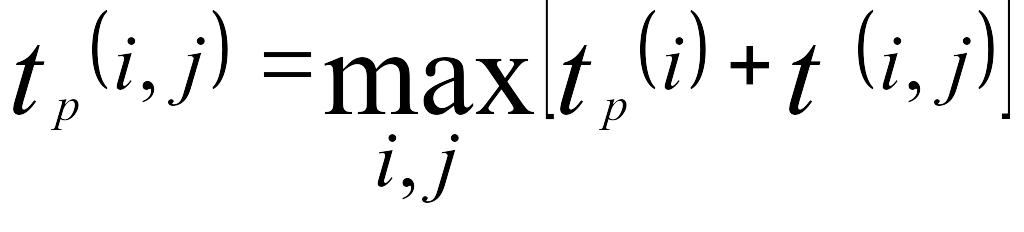Задержка совершения события i по отношению к своему раннему сроку не отразится на сроке свершения завершающего события (а значит, и на сроке выполнения комплекса работ) до тех пор, пока сумма срока свершения этого события и продолжительности (длины) максимального из последующих за ним путей не превысит длины критического пути.

Поэтому поздний (или предельный) срок t_П (i) свершения i-го события равен:

,

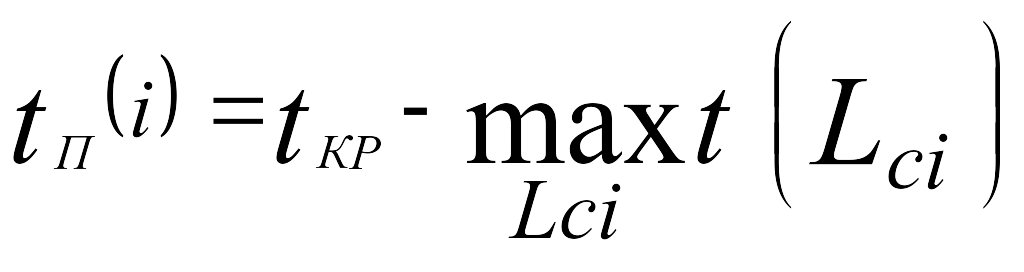где L_ci - любой путь, следующий за i-м событием, т.е. путь от i-го до завершающего события сети.

Если событие i имеет несколько последующих путей, а следовательно, несколько последующих событий j, то поздний срок свершения события i можно найти по следующей формуле:

.

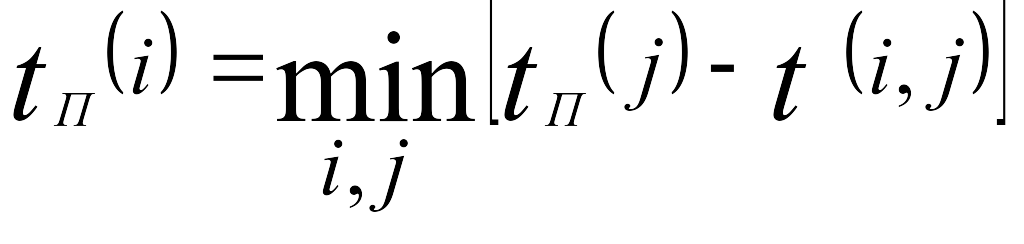Резерв времени R(i) i-го события определяется как разность между поздним и ранним сроками его свершения

.

Резерв времени события показывает, на какой допустимый период времени можно задержать наступление этого события, не вызывая при этом увеличения срока выполнения комплекса работ.

Критические события резервов времени не имеют, так как любая задержка в свершении события, лежащего на критическом пути, вызовет такую же задержку в свершении завершающего события.

Из этого следует, что для того, чтобы определить длину и топологию критического пути, вовсе не обязательно перебирать все полные пути сетевого графика и определять их длины. Определив ранний срок наступления завершающего события сети, мы тем самым определяем длину критического пути, а, выявив события с нулевыми резервами времени, определяем его топологию.

Теперь можно перейти к параметрам работ.

Отдельная работа может начаться (и окончиться) в ранние, поздние или другие промежуточные сроки. В дальнейшем при оптимизации графика возможно любое размещение работы в заданном интервале.

Очевидно, что ранний срок t_рн(i, j) начала работы (i, j) совпадает с ранним сроком наступления начального события i, т.е.:

Тогда ранний срок t_ро(i, j) окончания работы (i, j) определяется по формуле:

.

Ни одна работа не может окончиться позже позднего допустимого срока своего конечного события i. Поэтому поздний срок t_по(i, j) окончания работы

(i, j) определяется соотношением,

,

а поздний срок t_пн(i, j) начала этой работы - соотношением:

.

Таким образом, в рамках сетевой модели моменты начала и окончания работы тесно связаны с соседними событиями ограничениями.

---

Прежде чем рассматривать резервы времени работ, обратимся к резерву времени пути. Такие резервы имеют все некритические пути. Резерв времени пути R(L) определяется как разность между длиной критического и рассматриваемого пути:

.

Он показывает, на сколько в сумме могут быть увеличены продолжительности всех работ, принадлежащих этому пути. Если затянуть выполнение работ, лежащих на этом пути, на время большее чем R(L), то критический путь переместится на путь L.

Отсюда можно сделать вывод, что любая из работ пути L на его участке, не совпадающем с критическим путем (замкнутым между двумя событиями критического пути), обладает резервом времени.

Среди резервов времени работ выделяют четыре разновидности.

Полный резерв времени R_П (i, j) работы (i, j) показывает, на сколько можно увеличить время выполнения данной работы при условии, что срок выполнения комплекса работ не изменится. Полный резерв времени определяется по формуле:

.

Полный резерв времени работы равен резерву максимального из путей, проходящего через данную работу. Этим резервом можно располагать при выполнении данной работы, если ее начальное событие свершится в самый ранний срок, и можно допустить свершение конечного события в его самый поздний срок.

Важным свойством полного резерва времени работы является то, что он принадлежит не только этой работе, но и всем полным путям, проходящим через нее. При использовании полного резерва времени только для одной работы резервы времени остальных работ, лежащих на максимальном пути, проходящим через нее, будут полностью исчерпаны. Резервы времени работ, лежащих на других (немаксимальных по длительности) путях, проходящих через работу, сократятся соответственно на величину использованного резерва.

Остальные резервы времени работы являются частями ее полного резерва.

Частный резерв времени первого вида R₁ работы (i, j) есть часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом позднего срока ее начального события. Этим резервом можно располагать при выполнении данной работы в предположении, что ее начальное и конечное события свершаются в свои самые поздние сроки.

Частный резерв времени первого вида находится по формуле:

или

.

Частный резерв времени второго вида, или свободный резерв времени R_C работы (i, j) представляет часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом раннего срока ее конечного события. Этим резервом можно располагать при выполнении данной работы в предположении, что ее начальное и конечное события свершаются в свои самые ранние сроки. Свободный резерв времени находится по формуле:

или

.

Свободным резервом времени можно пользоваться для предотвращения случайностей, которые могут возникнуть в ходе выполнения работ. Если планировать выполнение работ по ранним срокам их начала и окончания, то всегда будет возможность при необходимости перейти на поздние сроки начала и окончания работ.

---

Независимый резерв времени R_Н работы (i, j) - часть полного резерва времени, получаемая для случая, когда все предшествующие работы заканчиваются в поздние сроки, а все последующие работы начинаются в ранние сроки.

или

.

Использование независимого резерва времени не влияет на величину резервов времени других работ. Независимые резервы стремятся использовать тогда, когда окончание предыдущей работы произошло в поздний допустимый срок, а последующие работы хотят выполнить в ранние сроки. Если величина независимого резерва равна нулю или положительна, то такая возможность есть. Если же величина R_Н (i, j) отрицательна, то этой возможности нет, так как предыдущая работа еще не оканчивается, а последующая уже должна начаться. Поэтому отрицательное значение независимого резерва времени не имеет реального смысла. А фактически независимый резерв имеют лишь те работы, которые не лежат на максимальных путях, проходящих через их начальные и конечные события.

Следует отметить, что резервы времени работы (i, j) могут состоять из двух временных отрезков, если интервал продолжительности работы t(i, j) занимает промежуточную позицию между двумя его крайними положениями, изображенными на графиках.

Таким образом, если частный резерв времени первого вида может быть использован на увеличение продолжительности данной и последующих работ без затрат резерва времени предшествующих работ, а свободный резерв времени - на увеличение продолжительности данной и предшествующих работ без нарушения резерва времени последующих работ, то независимый резерв времени может быть использован для увеличения продолжительности только данной работы.

Работы, лежащие на критическом пути, так же как и критические события резервов времени не имеют.

Если на критическом пути лежит начальное событие i, то:

.

Если на критическом пути лежит конечное событие j, то:

.

Если на критическом пути лежат начальное и конечное события i и j, но сама работа не принадлежит этому пути, то:

.

Эти соотношения можно использовать при проверке правильности расчетов резервов времени отдельных работ.

Анализ и оптимизация сетевых планов

После нахождения критического пути и резервов времени работ должен быть проведен всесторонний анализ сетевого графика и приняты меры по его оптимизации. Это весьма важный этап в разработке сетевых графиков раскрывает основную идею СПУ. Он заключается в приведении сетевого графика в соответствие с заданными сроками и возможностями организации, разрабатывающей проект.

В практике стратегического планирования в зависимости от конкретных условий, оптимизация сетевых графиков подразделяется на частную и комплексную. Основными видами частной оптимизации являются:

1. Минимизация времени выполнения комплекса планируемых работ при заданной стоимости проекта.

2. Минимизация стоимости всего комплекса работ при заданном времени выполнения проекта.

---

Комплексная оптимизация сетевых моделей состоит в нахождении наилучших соотношений показателей затрат экономических ресурсов и сроков выполнения планируемых работ. В условиях рыночной системы в качестве критерия оптимальности сетевых систем планирования могут быть выбраны такие важные экономические показатели, как максимальная прибыль, минимальный расход ресурсов и т.п.

В первую очередь, следует рассмотреть анализ и оптимизацию сетей, в которых заданы только оценки продолжительности работ. В этом случае главной задачей является минимизация затрат времени на выполнение как отдельных процессов, так и всего комплекса работ.

Анализ сетевого графика начинается с анализа топологии сети, включающего контроль построения сетевого графика, установление целесообразности выбора работ, степени их расчленения.

Затем проводятся классификация и группировка работ по величинам резервов. Следует отметить, что величина полного резерва времени далеко не всегда может достаточно точно характеризовать, насколько напряженным является выполнение той или иной работы некритического пути. Все зависит от того, на какую последовательность работ распространяется вычисленный резерв, какова продолжительность этой последовательности.

Определить степень трудности выполнения в срок каждой группы работ некритического пути можно с помощью коэффициента напряженности работ.

Коэффициентом напряженности К_Н работы (i, j) называется отношение продолжительности несовпадающих (заключенных между одними и теми же событиями) отрезков пути, одним из которых является путь максимальной продолжительности, проходящий через данную работу, а другим - критический путь:

,

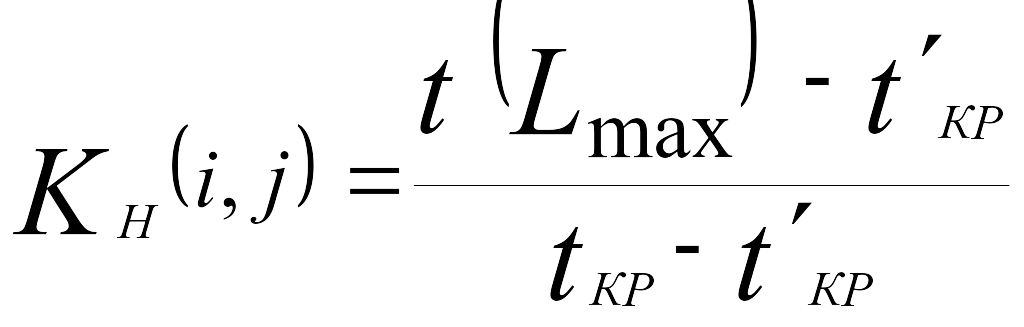где t(L_max) - продолжительность максимального пути, проходящего через работу (i, j);

t_КР - продолжительность (длина) критического пути;

t'_КР - продолжительность отрезка рассматриваемого пути, совпадающего с критическим путем [9, стр.317].

Формулу нахождения коэффициента напряженности легко можно привести к виду:

,

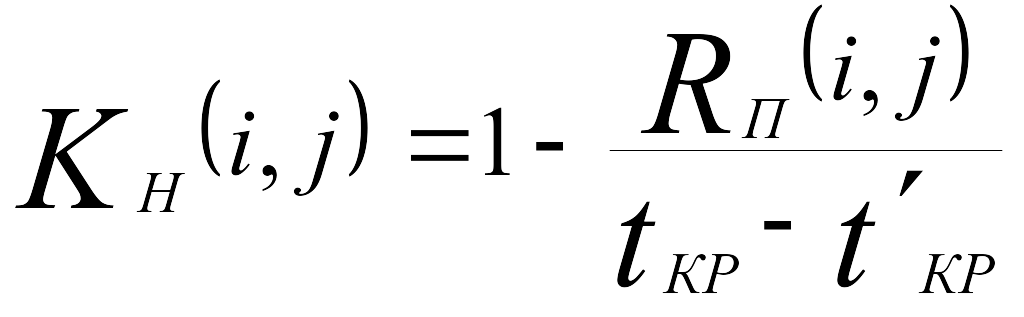где R_П (i, j) - полный резерв времени работы (i, j).

Коэффициент напряженности К_Н(i, j) может изменяться в пределах от 0 (для работ, у которых отрезки максимального из путей, не совпадающие с критическим путем, состоят из фиктивных работ нулевой продолжительности) до 1 (для работ критического пути).

Чем ближе к единице коэффициент напряженности, тем сложнее выполнить данную работу в установленные сроки. Чем ближе К_Н (i, j) к нулю, тем большим относительным резервом обладает максимальный путь, проходящий через данную работу.

Работы могут обладать полными одинаковыми резервами, но степень напряженности сроков их выполнения, выражаемая коэффициентом напряженности К_Н (i, j), может быть различна. И наоборот, полным различным резервам могут соответствовать одинаковые коэффициенты напряженности. Другими словами, следует учитывать, что больший полный резерв одной работы (по сравнению с другой) не обязательно свидетельствует о меньшей степени напряженности ее выполнения. Это объясняется разным удельным весом полных резервов работ в продолжительности отрезков максимальных путей, не совпадающих с критическим путем.

---

Смотрите также файлы

• Пример инновационного проекта.docx

• Отбор и оценка проектов.pdf

• Организационные структуры проектно ориентированных организаций.docx

• Методические рекомендации по оценке эфективности инвестиционных проектов.doc

• Американ. стандарт 4-е издание.pdf