ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 15.06.2020
Просмотров: 240
Скачиваний: 2
, (2.56)
.
Определяем максимальное усилие, приходящееся на крайние болты
Условие прочности не выполняется. Добавляем по одному вертикальному ряду болтов с каждой стороны стыка.
Условие прочности выполнено.

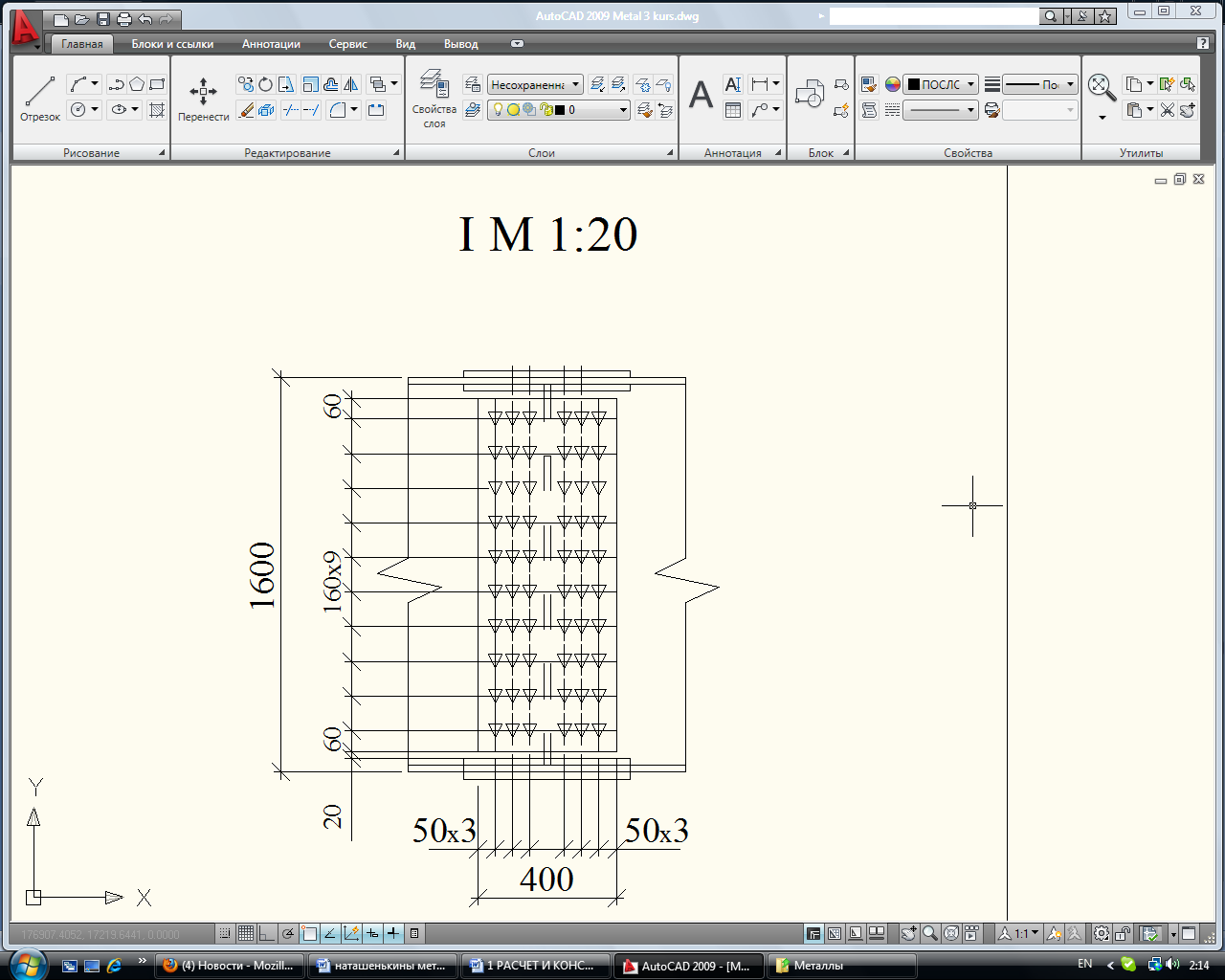
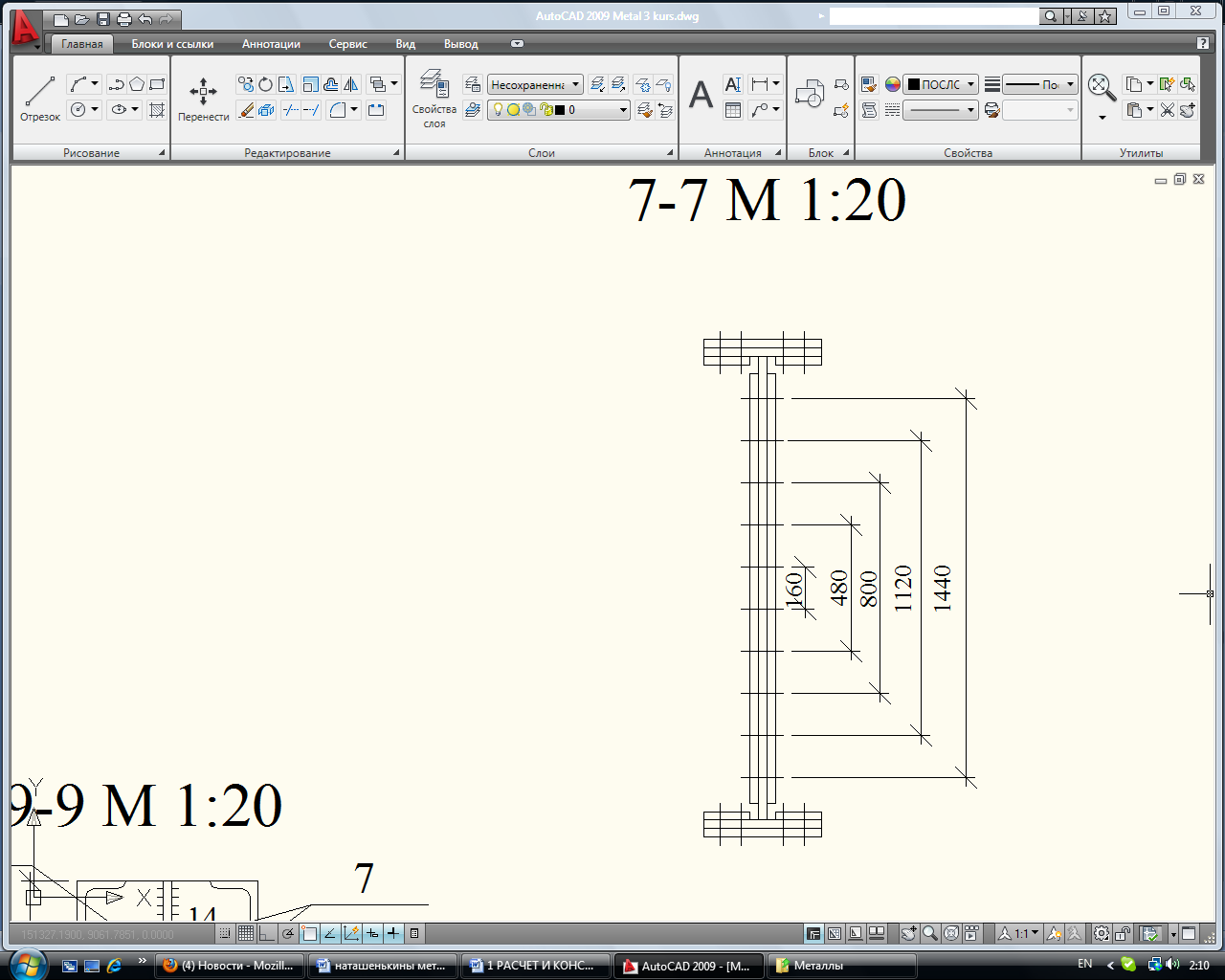
Рисунок 12 – Размещение болтов на монтажном стыке главной балки
3 РАСЧЕТ И КОНСТРУИРОВАНИЕ ЦЕНТРАЛЬНО СЖАТОЙ КОЛОННЫ
Колонна проектируется сквозного сечения, состоящая из двух ветвей, соединенных между собой планками. Сечение одной ветви – прокатный двутавр.
Рисунок 13 –Колонна
3.1 Определение расчетной нагрузки
Определяем расчетную нагрузку на колонну
, (3.1)
где G- вес главной балки;
Qmax – максимальная нагрузка от поперечной силы главной балки.
, (3.2)
где А- площадь поперечного сечения главной балки, м2;
= 78,2 кН/м3
– плотность стали;
l – пролет главной балки.
А=38*2,5*2+160*1,5=430 см2=0,043 м2 .
Тогда по формуле (3.2) получим:
кН.
По формуле (3.1) получим:
=2590,79
кН.
Определяем расчетные длины колонны в плоскости и из плоскости конструкции:
, (3.3)
.
-
коэффициенты защемления балки
.
Фактическая длина колонны:
, (3.4)
где
- отметка верха настила;
-
толщина настила;
- высота главной балки;
- глубина защемления колонны.
м.
3.2. Подбор сечения колонны
Требуемая площадь сечения
,
(3.5)
где
- предельное значение продольного
изгиба,
=0,7
– 0,8
Требуемая площадь одной ветви
(3.6)
Рисунок 14 – Геометрические характеристики колонны
Рисунок 15 - Соединение двух ветвей колонны планками
Принимаем двутавр № 40 со следующими характеристиками:
,
,
,
,
,
.
Определяем гибкость относительно материальной оси
(3.7)
-
предельная гибкость
Требуемая гибкость относительно свободной оси:
,
(3.8)
где λ1
– гибкость одной ветви
Также λу определяется следующим образом:
, (3.9)
Отсюда требуемый радиус инерции сечения
Требуемая ширина сечения
, (3.10)
- коэффициент, зависящий от формы сечения.
Принимаем ширину сечения кратной 10 мм b=350 мм и проверяем возможность размещения на ней минимального зазора между ветвями 150 мм.
Что достаточно, оставляем сечение шириной 35 см.
Определяем геометрические характеристики подобранного сечения:
(3.11)
Определяем радиус инерции относительно материальной оси
(3.12)
По формуле (3.9) получаем:
<
λx=57.64
Проверку производим по большей гибкости λx.
Проверка устойчивости:
По
и
находим требуемое значение
(3.13)
- условие выполняется.
3.3. Расчет соединительных планок
Ветви колонны
соединяем при помощи листовых планок
шириной
см. Для сварки применяем электроды Э
46.
Расстояние между
планками определяем по предельной
гибкости ветви :
, (3.14)
.
Принимаем расстояние между планками равным 60 см.
(3.15)
Определяем условную поперечную силу, которая приходится на 2 плоскости планок:
, (3.16)
.
Определяем усилия, действующие на 1 планку:
, (3.17)
, (3.18)
, (3.19)
.
Определяем касательное напряжение в сварном шве:
, (3.20)
где
- катет сварного шва;
-
коэффициент сварки;
кН/см2
-расчетное сопротивление углового
сварного шва по металлу шва.
кН/см2
Определяем нормальные напряжения в сварном шве:
, (3.21)
.
Определяем приведенные напряжения в шве:
, (3.22)
.
Прочность шва обеспечена
3.4 Расчет и конструирование базы колонны
Нагрузку на базу принимаем с учетом веса двух ветвей колонны.
(3.23)
кН.
Требуемая площадь опорной плиты:
, (3.24)
где Rф – расчетное сопротивление фундамента, кН/см2, для В15;
ζ – коэффициент, учитывающий влияние металлической плиты (1,1…1,3);
Rб – расчетное сопротивление бетона на сжатие, 0,85 кН/см2.
.
Рисунок 16 – Геометрические параметры траверсы
Конструктивно принимаем толщину траверсы равной 12 мм. Определяем длину плиты:
мм. (3.25)
Определяем ширину плиты:
см.
Принимаем
см.
Проверяем достаточность этого размера для размещения ветвей колонны:
, (3.26)
где
- высота двутавра;
мм- толщина траверсы.
Колонна размещается на плите.
Разбиваем плиту на участки в зависимости от их защемления и определяем моменты на этих участках.
Напряжение под плитой:
(3.27)
Определяем требуемую толщину плиты
(3.28)
Принимаем
.
Из условия прочности на срез угловых сварных швов определяем высоту траверсы:
(3.29)
Принимаем
см.
3.5. Расчет оголовка колонны
Рисунок 16 – Оголовок колонны
Толщину ребра оголовка определяем из условия смятия ребра опорной реакцией главной балки:
, (3.30)
где Rр
–расчетное сопротивление стали на
смятие,
,
Run – нормальное сопротивление по пределу прочности, кН/см2.
.
Тогда принимаем
толщину ребра оголовка колонны
=20
мм.
Определяем высоту ребра по формуле (3.29):
Принимаем высоту ребра 80 см, толщину плиты оголовка tпл=30 мм.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. СНиП II-23-81 Стальные конструкции. Нормы проектирования. М. ЦИТП. 1990.
2. Губенко Л. А. Справочные материалы к расчету и подбору сечений элементов металлических конструкций / Л. А. Губенко, В. А. Катаев, Е. А. Мошникова. – Архангельск: Изд-во АГТУ, 2007. – 44 с.
3. Губенко Л.А. Расчет конструкций балочной клетки / Губенко Л.А.,
Никитина Т.А. - Архангельск: Изд-во АГТУ, 2011.