ВУЗ: Санкт-Петербургский государственный технологический институт (технический университет)
Категория: Методичка
Дисциплина: Автоматизированное проектирование
Добавлен: 15.11.2018
Просмотров: 3209
Скачиваний: 6

16
Оценить влияние на выход целевого компонента:
- изменения концентрации метана от 1 до 5 моль/л
- изменения температуры реакции от Т = 900 К до Т = 1400 К.
Вариант 8
В газофазном реакторе непрерывного действия происходит процесс
получения ацетона (CH
3
COCH
3
) из окиси пропилена (С
3
Н
6
О) по следующему
механизму:
С
3
Н
6
О
1
К
CH
3
COCH
3
С
3
Н
6
О
2
К
CH
3
CH
2
CHO
Разработать математическую модель кинетики процесса и получить
решение при следующих условиях:
- объем аппарата составляет 1м
3
; расход реагентов – 0,05 м
3
/мин;
- интервал времени τ = 100 мин; шаг по времени Δt = 1 мин;
- начальная концентрация С
С3Н6О
= 1,0 Кмоль/м
3
;
- предэкспоненциальные множители: К
01
=2; К
02
=2;
- энергия активации Е
1
= 20000 Дж/моль, Е
2
= 24000 Дж/моль;
- температура Т = 700 K.
Частные порядки по компонентам в реакциях равны единице.
Оценить влияние на выход целевого компонента:
- изменения температуры в реакторе от 700 до 1000 K с шагом 100 K;
-
изменения объема реактора от 1 до 3 м
3
.
Выбрать наилучший вариант проведения процесса с точки зрения получения
максимального выхода целевого продукта.
Вариант 9
В
периодическом реакторе идеального смешения происходит процесс
получения ацетона (CH
3
COCH
3
) из окиси пропилена (С
3
Н
6
О) по следующему
механизму:
С
3
Н
6
О
1
К
CH
3
COCH
3
С
3
Н
6
О
2
К
CH
3
CH
2
CHO
Разработать математическую модель кинетики процесса и получить
решение при следующих условиях:
- интервал времени τ= 100 мин; шаг по времени Δt = 1 мин;
- начальная концентрация С
С3Н6О
= 1,0 Кмоль/м
3
;
- предэкспоненциальные множители: К
01
=2; К
02
=2;
- энергия активации Е
1
= 20000 Дж/моль, Е
2
= 24000 Дж/моль;
- температура Т = 700 K.
Частные порядки по компонентам в реакциях равны единице.
Оценить влияние на выход целевого компонента:
- изменения концентрации окиси пропилена от 1 до 5 моль/м
3
;

17
- изменения температуры реакции от Т = 500 К до Т = 900 К.
Определить время пребывания τ
опт
, обеспечивающее максимально возможный
выход целевого продукта (ацетона) для всех вариантов исследования процесса.
Рассчитать рабочий объем реактора V для производительности аппарата
G = 0,2 м
3
/мин.
V = τ
опт
·G
Вариант 10
В
периодическом реакторе идеального смешения происходит процесс
получения аммиачной селитры (NH
4
NO
3
) по следующему механизму:
NH
3
+ НNO
3
1
К
NH
4
NO
3
NH
4
NO
3
2
К
NO
2
+ 2H
2
O
Разработать математическую модель кинетики процесса и получить
решение при следующих условиях:
- интервал времени τ = 300 мин; шаг по времени Δt = 1 мин;
- начальные концентрации С
NH3
= 1,0 моль/л;
С
HNO3
= 1,0 моль/л;
- предэкспоненциальные множители: К
01
=5530; К
02
=2∙10
13
;
- энергия активации Е
1
= 48650 Дж/моль, Е
2
= 137000 Дж/моль;
- температура Т = 200 ºС.
Частные порядки по компонентам во всех реакциях равны единице.
Оценить влияние на выход целевого компонента:
- изменения концентрации аммиака от 1 до 5 моль/л;
- изменения температуры реакции от Т = 170 ºС до Т = 230 ºС.
Определить время пребывания τ
опт
, обеспечивающее максимально возможный
выход целевого продукта для всех вариантов исследования процесса.
Рассчитать рабочий объем реактора V для производительности аппарата
G =200 л/мин.
V = τ
опт
·G
1.6 Пример выполнения контрольной работы № 1
В реакторе периодического действия протекает процесс получения
продукта «В», для которого предложен следующий механизм реакций:
A
C
B
E
D
B
C
B
A
K
K
K
3
2
1
2
2
Разработать математическую модель кинетики процесса и получить
решение при следующих условиях:
- интервал времени τ = 50 мин; шаг по времени Δt = 0,5 мин;

18
- начальные концентрации С
OA
= 0,800 моль/л;
- предэкспоненциальные множители:
к
0i
={0,2·10
14
1/мин; 9·10
15
1/мин; 0,5·10
14
л
2
/(моль
2
·мин)};
- энергия активации Е
1
= 74 кДж/моль, Е
2
= 89 кДж/моль, Е
3
= 80
кДж/моль;
- температура Т = -3ºС.
Решение примера показано на рисунке 2.1.
Прежде чем записать решение данной задачи в MathCad, необходимо
сформировать структуру математической модели кинетики. Для этого
составляются матрицы стехиометрических коэффициентов и частных порядков,
а также уравнения для скоростей реакций и уравнения для скоростей изменения
концентраций компонентов. Для
рассматриваемого
примера
матрица
стехиометрических коэффициентов будет иметь следующий вид:
0
0
1
2
1
1
1
0
1
0
0
0
1
2
1
S
.
Матрица частных порядков примет следующую форму:
0
0
1
2
0
0
0
0
1
0
0
0
0
0
1
P
.
В соответствии с матрицами записываются уравнения для скоростей
реакций:
A
1
C
k
w
1
;
B
2
C
k
w
2
;
C
B
3
C
C
k
w
2
3
.
Уравнения для скоростей изменения концентраций компонентов
выглядят следующим образом:
2
2
3
1
3
2
1
3
1
2
2
w
dt
dC
w
dt
dC
w
w
dt
dC
w
w
w
dt
dC
w
w
dt
dC
E
D
C
B
A

19
При записи уравнений в MathCad концентрация компонента A
обозначается буквой c
0
, компонента B − c
1
, компонента C − c
2
. Для решения
системы
обыкновенных
дифференциальных
уравнений
используется
встроенная функция Rkadapt (метод Рунге − Кутты с переменным шагом),
аргументами которой являются вектор-столбец начальных концентраций c0,
начальное и конечное значение диапазона времени исследования (в данном
случае от 0 до 50 минут), количество шагов по времени (в данном случае 100
шагов) и название решаемой системы (в данном случае она называется D).
Рисунок 1.1 – Расчет примера для контрольной работы № 1
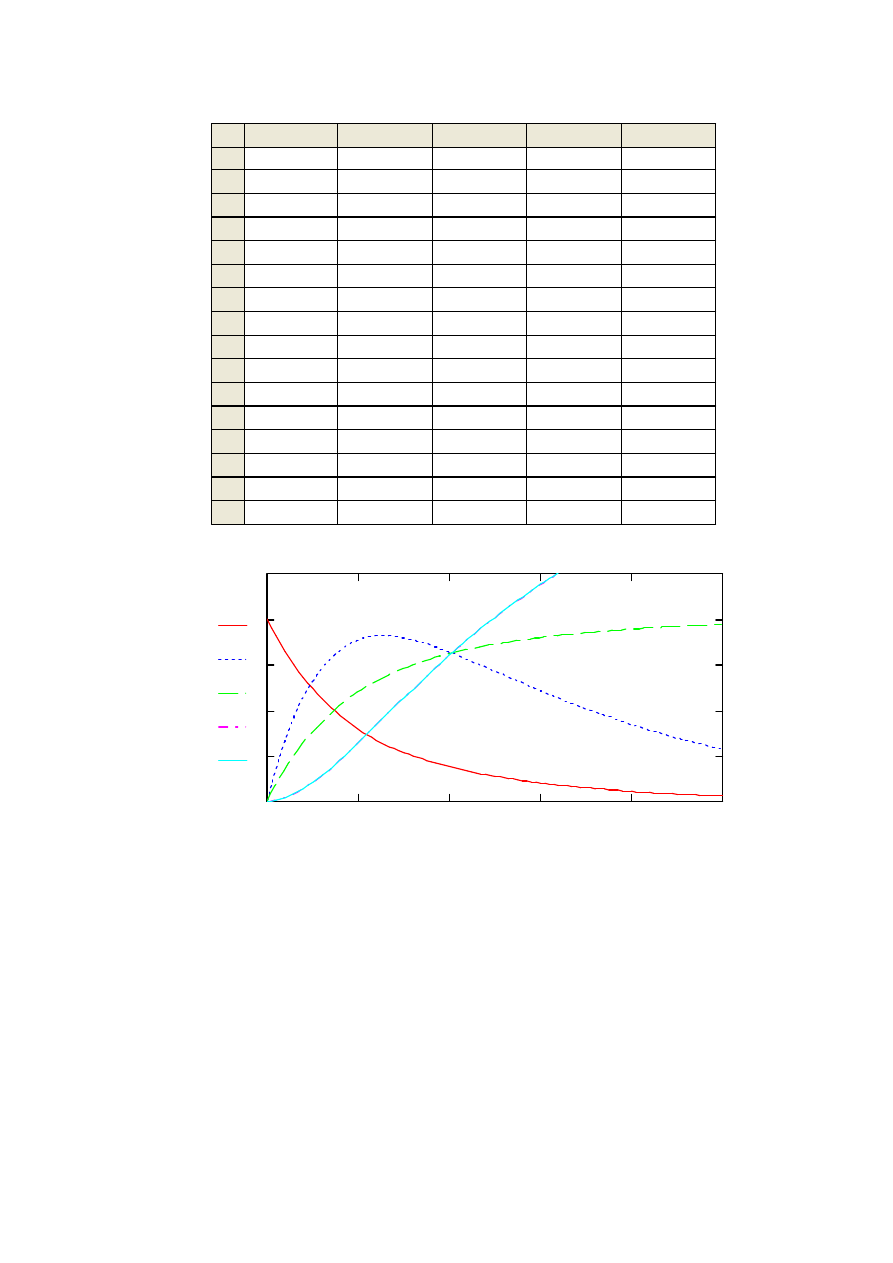
На рисунке 1.2 представлены результаты расчета рассмотренной задачи.
В нулевом столбце таблицы находятся значения текущего времени (поэтому
время на оси абсцисс графика концентраций обозначено как u
<0>
); в остальных
столбцах выводятся расчетные концентрации компонентов реакционной
системы. В соответствии с содержимым этих столбцов строятся графики,
приведенные на рисунке 1.2.
k01
0.2 10
14
k02
9 10
15
k03
0.5 10
14
E1
74000
E2
89000
E3
80000
R
8.31
T
3
273.15
n
100
c0
0.8
0
0
0
0
k1
k01 e
E1
R T
k2
k02 e
E2
R T
k3
k03 e
E3
R T
k3
0.017
D t c
(
)
k1
c
0
k3 c
1
2
c
2
2k1 c
0
k2 c
1
2
k3 c
1
2
c
2
k1 c
0
k3
c
1
2
c
2
k2 c
1
k2 c
1
k1
0.097
k2
0.055
u
Rkadapt c0 0
50
n
D
(
)
20
Рисунок 1.2 – Результаты расчета примера для контрольной работы № 1
u
0
1
2
3
4
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0
0.8
0
0
0
0.5
0.762
0.074
0.038
-3
1.029·10
1
0.726
0.143
0.074
-3
4.013·10
1.5
0.692
0.207
0.108
-3
8.806·10
2
0.659
0.266
0.141
0.015
2.5
0.628
0.32
0.172
0.023
3
0.599
0.369
0.201
0.033
3.5
0.571
0.415
0.229
0.043
4
0.544
0.456
0.256
0.055
4.5
0.519
0.493
0.281
0.068
5
0.495
0.527
0.305
0.082
5.5
0.473
0.558
0.327
0.097
6
0.451
0.585
0.349
0.113
6.5
0.431
0.609
0.369
0.129
7
0.412
0.631
0.388
0.146
7.5
0.394
0.649
0.406
...
0
10
20
30
40
50
0
0.2
0.4
0.6
0.8
u
1
u
2
u
3
u
4
u
5
u
0