Файл: 4.2. Принципы и подходы к построению математических моделей. Этапы построения математических моделей.docx
ВУЗ: Смоленский областной казачий институт промышленных технологий и бизнеса
Категория: Лекция
Дисциплина: Моделирование систем
Добавлен: 19.11.2018
Просмотров: 693
Скачиваний: 12
-
ПРИНЦИПЫ И ПОДХОДЫ К ПОСТРОЕНИЮ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
Математическое моделирование многие считают скорее искусством, чем стройной и законченной теорией. Здесь очень велика роль опыта, интуиции и других интеллектуальных качеств человека. Поэтому невозможно написать достаточно формализованную инструкцию, определяющую, как должна строиться модель той или иной системы. Тем не менее отсутствие точных правил не мешает опытным специалистам строить удачные модели. К настоящему времени уже накоплен значительный опыт, дающий основание сформулировать некоторые принципы и подходы к построению моделей. При рассмотрении порознь каждый из них может показаться довольно очевидным. Но совокупность взятых вместе принципов и подходов далеко не тривиальна. Многие ошибки и неудачи в практике моделирования являются прямым следствием нарушения этой методологии.
Принципы определяют те общие требования, которым должна удовлетворять правильно построенная модель. Рассмотрим эти принципы.
1. Адекватность. Этот принцип предусматривает соответствие модели целям исследования по уровню сложности и организации, а также соответствие реальной системе относительно выбранного множества свойств. До тех пор, пока не решен вопрос, правильно ли отображает модель исследуемую систему, ценность модели незначительна.
2. Соответствие модели решаемой задаче. Модель должна строиться для решения определенного класса задач или конкретной задачи исследования системы. Попытки создания универсальной модели, нацеленной на решение большого числа разнообразных задач, приводят к такому усложнению, что она оказывается практически непригодной. Опыт показывает, что при решении каждой конкретной задачи нужно иметь свою модель, отражающую те аспекты системы, которые являются наиболее важными в данной задаче. Этот принцип связан с принципом адекватности.
3. Упрощение при сохранении существенных свойств системы. Модель должна быть в некоторых отношениях проще прототипа - в этом смысл моделирования. Чем сложнее рассматриваемая система, тем по возможности более упрощенным должно быть ее описание, умышленно утрирующее типичные и игнорирующее менее существенные свойства. Этот принцип может быть назван принципом абстрагирования от второстепенных деталей.
4. Соответствие между требуемой точностью результатов моделирования и сложностью модели. Модели по своей природе всегда носят приближенный характер. Возникает вопрос, каким должно быть это приближение. С одной стороны, чтобы отразить все сколько-нибудь существенные свойства, модель необходимо детализировать. С другой стороны, строить модель, приближающуюся по сложности к реальной системе, очевидно, не имеет смысла. Она не должна быть настолько сложной, чтобы нахождение решения оказалось слишком затруднительным. Компромисс между этими двумя требованиями достигается нередко путем проб и ошибок. Практическими рекомендациями по уменьшению сложности моделей являются:
• изменение числа переменных, достигаемое либо исключением несущественных переменных, либо их объединением. Процесс преобразования модели в модель с меньшим числом переменных и ограничений называют агрегированием. Например, все типы ЭВМ в модели гетерогенных сетей можно объединить в четыре типа - ПЭВМ, рабочие станции, большие ЭВМ (мейнфреймы), кластерные ЭВМ;
• изменение природы переменных параметров. Переменные параметры рассматриваются в качестве постоянных, дискретные - в качестве непрерывных и т.д. Так, условия распространения радиоволн в модели радиоканала для простоты можно принять постоянными;
• изменение функциональной зависимости между переменными. Нелинейная зависимость заменяется обычно линейной, дискретная функция распределения вероятностей - непрерывной;
• изменение ограничений (добавление, исключение или модификация). При снятии ограничений получается оптимистичное решение, при введении – пессимистичное. Варьируя ограничениями, можно найти возможные граничные значения эффективности. Такой прием часто используется для нахождения предварительных оценок эффективности решений на этапе постановки задач;
• ограничение точности модели. Точность результатов модели не может быть выше точности исходных данных.
5. Баланс погрешностей различных видов. В соответствии с принципом баланса необходимо добиваться, например, баланса систематической погрешности моделирования за счет отклонения модели от оригинала и погрешности исходных данных, точности отдельных элементов модели, систематической погрешности моделирования и случайной погрешности при интерпретации и осреднении результатов.
6. Многовариантность реализации элементов модели. Разнообразие реализации одного и того же элемента, отличающихся по точности (а следовательно, и по сложности), обеспечивает регулирование соотношения «точность/ сложность».
7. Блочное строение. При соблюдении принципа блочного строения облегчается разработка сложных моделей и появляется возможность использования накопленного опыта и готовых блоков с минимальными связями между ними. Выделение блоков производится с учетом разделения модели по этапам и режимам функционирования системы. К примеру, при построении модели для системы радиоразведки можно выделить модель работы излучателей, модель обнаружения излучателей, модель пеленгования и т.д.
В зависимости от конкретной ситуации возможны следующие подходы к построению моделей
• непосредственный анализ функционирования системы;
• проведение ограниченного эксперимента на самой системе;
• использование аналога;
• анализ исходных данных.
Имеется целый ряд систем, которые допускают проведение непосредственных исследований по выявлению существенных параметров и отношений между ними. Затем либо применяются известные математические модели, либо они модифицируются, либо предлагается новая модель. Таким образом, например, можно вести разработку модели для направления связи в условиях мирного времени.
При проведении эксперимента выявляются значительная часть существенных параметров и их влияние на эффективность системы. Такую цель преследуют, например, все командно-штабные игры и большинство учений.
Если метод построения модели системы не ясен, но ее структура очевидна, то можно воспользоваться сходством с более простой системой, модель для которой существует.
К построению модели можно приступить на основе анализа исходных данных, которые уже известны или могут быть получены. Анализ позволяет сформулировать гипотезу о структуре системы, которая затем апробируется. Так появляются первые модели нового образца иностранной техники при наличии предварительных данных об их технических параметрах.
Разработчики моделей находятся под действием двух взаимно противоречивых тенденций: стремления к полноте описания и стремления к получению требуемых результатов возможно более простыми средствами. Достижение компромисса ведется обычно по пути построения серии моделей, начинающихся с предельно простых и восходящих до высокой сложности (существует известное правило: начинай с простых моделей, а далее усложняй). Простые модели помогают глубже понять исследуемую проблему. Усложненные модели используются для анализа влияния различных факторов на результаты моделирования. Такой анализ позволяет исключать некоторые факторы из рассмотрения.
Сложные системы требуют разработки целой иерархии моделей, различающихся уровнем отображаемых операций. Выделяют такие уровни, как вся система, подсистемы, управляющие объекты и др.
Рассмотрим один конкретный пример - модель развития экономики (модель Харрода). Эта упрощенная модель развития экономики страны предложена английским экономистом Р. Харродом. В модели учитывается один определяемый фактор - капитальные вложения, а состояние экономики оценивается через размер национального дохода.
Для математической постановки задачи введем следующие обозначения:
• Yt - национальный доход в год t;
• Кt - производственные фонды в год t;
• Сt - объем потребления в год t;
• St - объем накопления в год t;
• Vt - капитальные вложения в год t .
Будем предполагать, что функционирование экономики происходит при выполнении следующих условий:
• условие баланса доходов и расходов за каждый год
Yt = Сt + St ;
• условие исключения пролеживания капитала
St = Vt ;
• условие пропорционального деления национального годового дохода
St = aVt .
Два условия принимаются для характеристики внутренних экономических процессов. Первое условие характеризует связь капитальных вложений и общей суммы производственных фондов, второе - связь национального годового дохода и производственных фондов.
Капитальные вложения в год t могут рассматриваться как прирост производственных фондов или производная от функции производственные фонды принимается как капитальные годовые вложения:
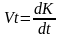
Национальный доход в каждый год принимается как отдача производственных фондов с соответствующим нормативным коэффициентом фондоотдачи:
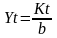
Соединяя условия задачи, можно получить следующие соотношения:
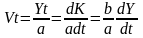
Отсюда следует итоговое уравнение Харрода:
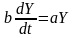
Его решением является экспоненциальное изменение национального дохода по годовым интервалам:
Yt = Y0 eat/b
Несмотря на упрощенный вид математической модели, ее результат может быть использован для укрупненного анализа национальной экономики. Параметры а и b могут стать параметрами управления при выборе плановой стратегии развития в целях максимального приближения к предпочтительной траектории изменения национального дохода или для выбора минимального интервала времени достижения заданного уровня национального дохода.
2. ЭТАПЫ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
Сущность построения математической модели состоит в том, что реальная система упрощается, схематизируется и описывается с помощью того или иного математического аппарата. Можно выделить следующие основные этапы построения моделей.
1. Содержательное описание моделируемого объекта. Объекты моделирования описываются с позиций системного подхода. Исходя из цели исследования устанавливаются совокупность элементов, взаимосвязи между элементами, возможные состояния каждого элемента, существенные характеристики состояний и соотношения между ними. Например, фиксируется, что если значение одного параметра возрастает, то значение другого - убывает и т.п. Вопросы, связанные с полнотой и единственностью набора характеристик, не рассматриваются. Естественно, в таком словесном описании возможны логические противоречия, неопределенности. Это исходная естественно-научная концепция исследуемого объекта. Такое предварительное, приближенное представление системы называют концептуальной моделью. Для того чтобы содержательное описание служило хорошей основой для последующей формализации, требуется обстоятельно изучить моделируемый объект. Нередко естественное стремление ускорить разработку модели уводит исследователя от данного этапа непосредственно к решению формальных вопросов. В результате построенная без достаточного содержательного базиса модель оказывается непригодной к использованию.
На этом этапе моделирования широко применяются качественные методы описания систем, знаковые и языковые модели.
2. Формализация операций. Формализация сводится в общих чертах к следующему. На основе содержательного описания определяется исходное множество характеристик системы. Для выделения существенных характеристик необходим хотя бы приближенный анализ каждой из них. При проведении анализа опираются на постановку задачи и понимание природы исследуемой системы. После исключения несущественных характеристик выделяют управляемые и неуправляемые параметры и производят символизацию. Затем определяется система ограничений на значения управляемых параметров. Если ограничения не носят принципиальный характер, то ими пренебрегают.
Дальнейшие действия связаны с формированием целевой функции модели. В соответствии с известными положениями выбираются показатели исхода операции и определяется примерный вид функции полезности на исходах. Если функция полезности близка к пороговой (или монотонной), то оценка эффективности решений возможна непосредственно по показателям исхода операции. В этом случае необходимо выбрать способ свертки показателей (способ перехода от множества показателей к одному обобщенному показателю) и произвести саму свертку. По свертке показателей формируются критерий эффективности и целевая функция.
Если при качественном анализе вида функции полезности окажется, что ее нельзя считать пороговой (монотонной), прямая оценка эффективности решений через показатели исхода операции неправомочна. Необходимо определять функцию полезности и уже на ее основе вести формирование критерия эффективности и целевой функции.
В целом замена содержательного описания формальным - это итеративный процесс.
3. Проверка адекватности модели. Требование адекватности находится в противоречии с требованием простоты, и это нужно учитывать при проверке модели на адекватность. Исходный вариант модели предварительно проверяется по следующим основным аспектам:
• Все ли существенные параметры включены в модель?
• Нет ли в модели несущественных параметров?
• Правильно ли отражены функциональные связи между параметрами?
• Правильно ли определены ограничения на значения параметров?
Для проверки рекомендуется привлекать специалистов, которые не принимали участия в разработке модели. Они могут более объективно рассмотреть модель и заметить ее слабые стороны, чем ее разработчики. Такая предварительная проверка модели позволяет выявить грубые ошибки. После этого приступают к реализации модели и проведению исследований. Полученные результаты моделирования подвергаются анализу на соответствие известным свойствам исследуемого объекта. Для установления соответствия создаваемой модели оригиналу используются следующие пути:
• сравнение результатов моделирования с отдельными экспериментальными результатами, полученными при одинаковых условиях;
• использование других близких моделей;
• сопоставление структуры и функционирования модели с прототипом.
Главным путем проверки адекватности модели исследуемому объекту выступает практика. Однако она требует накопления статистики, которая далеко не всегда бывает достаточной для получения надежных данных. Для многих моделей первые два пути приемлемы в меньшей степени. В этом случае остается один путь: заключение о подобии модели и прототипа делать на основе сопоставления их структур и реализуемых функций. Такие заключения не носят формального характера, поскольку основываются на опыте и интуиции исследователя.