Основные термины математического моделирования. Прежде чем начать рассматривать конкретные математические модели процессов принятия решений, необходимо определить основные термины, такие, как:

 - компоненты системы - части системы, которые могут быть вычленены из нее и рассмотрены отдельно;

 - независимые переменные – они могут изменяться, но это внешние величины, не зависящие от проходящих в системе процессов;

 - зависимые переменные - значения этих переменных есть результат (функция) воздействия на систему независимых внешних переменных;

 - управляемые (управляющие) переменные - те, значения которых могут изменяться исследователем;

 - эндогенные переменные – их значения определяются в ходе деятельности компонент системы (т.е. «внутри» системы);

 - экзогенные переменные - определяются либо исследователем, либо извне, т.е. в любом случае действуют на систему извне.

 При построении любой модели процесса принятия решения желательно придерживаться следующего плана действий:

 1) Сформулировать цели изучения системы;

 2) Выбрать те факторы, компоненты и переменные, которые являются наиболее существенными для данной задачи;

 3) Учесть тем или иным способом посторонние, не включенные в модель факторы;

 4) Осуществить оценку результатов, проверку модели, оценку полноты модели.

 Модели можно делить на следующие виды:

 1) Функциональные модели - выражают прямые зависимости между эндогенными и экзогенными переменными.

 2) Модели, выраженные с помощью систем уравнений относительно эндогенных величин. Выражают балансовые соотношения между различными экономическими показателями (например, модель межотраслевого баланса).

 3) Модели оптимизационного типа. Основная часть модели - система уравнений относительно эндогенных переменных. Но цель - найти оптимальное решение для некоторого экономического показателя (например, найти такие величины ставок налогов, чтобы обеспечить максимальный приток средств в бюджет за заданный промежуток времени).

 4) Имитационные модели - весьма точное отображение экономического явления. Математические уравнения при этом могут содержать сложные, нелинейные, стохастические зависимости.

 С другой стороны, модели можно делить на управляемые и прогнозные. Управляемые модели отвечают на вопрос: “Что будет, если ...?”; “Как достичь желаемого?”, и содержат три группы переменных: 1) переменные, характеризующие текущее состояние объекта; 2) управляющие воздействия - переменные, влияющие на изменение этого состояния и поддающиеся целенаправленному выбору; 3) исходные данные и внешние воздействия, т.е. параметры, задаваемые извне, и начальные параметры.

 В прогнозных моделях управление не выделено явно. Они отвечают на вопросы: “Что будет, если все останется по-старому?”

---

  Далее, модели можно делить по способу измерения времени на непрерывные и дискретные. В любом случае, если в модели присутствует время, то модель называется динамической. Чаще всего в моделях используется дискретное время, т.к. информация поступает дискретно: отчеты, балансы и иные документы приходят периодически. Но с формальной точки зрения непрерывная модель может оказаться более простой для изучения. Отметим, что в физической науке продолжается дискуссия о том, является ли реальное физическое время непрерывным или дискретным.

 Обычно в достаточно крупные социально-экономические модели входят материальный, финансовый и социальный разделы. Материальный раздел - балансы продуктов, производственных мощностей, трудовых, природных ресурсов. Это раздел, описывающий основополагающие процессы, это уровень, обычно слабо подвластный управлению, особенно быстрому, поскольку весьма инерционен.

 Финансовый раздел содержит балансы денежных потоков, правила формирования и использования фондов, правила ценообразования и.т.п. На этом уровне можно выделить много управляемых переменных. Они могут быть регуляторами. Социальный раздел содержит сведения о поведении людей. Этот раздел вносит в модели принятия решений много неопределенностей, поскольку трудно точно правильно учесть такие факторы как трудоотдача, структура потребления, мотивация и.т.п.

 При построении моделей, использующих дискретное время, часто применяют методы эконометрики. Среди них популярны регрессионные уравнения и их системы. Обычно используют уравнения не выше второго порядка, линейные по параметрам:

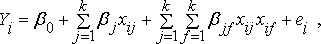
где    - переменная отклика;

    - факторы, от которых зависит  ;

    - коэффициенты, которые характеризуют взаимодействие между   и  ;

    - отражают взаимодействие между   и     ;

    - ошибка модели,

 i – номер наблюдения (измерения, опыта, анализа, испытания), i= 1, 2, , n

 j – номер фактора (независимой переменной), j = 1,2,…, k.

 Коэффициенты  ,   находят эконометрическими методами, например, методом наименьших квадратов. Различные системы регрессионных уравнений, построенные для решения практически важных задач, рассмотрены далее. Часто используют лаги (запаздывания в реакции). Для систем, нелинейных по параметрам, применение метода наименьших квадратов встречает трудности.

Классификация математических моделей

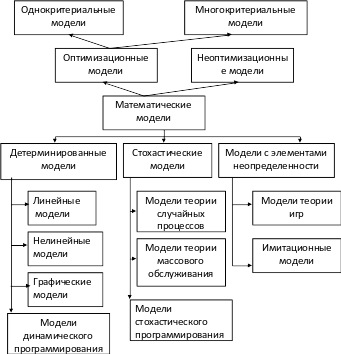В различных источниках приводятся разные варианты классификации математических моделей. Далее приводится наиболее удачная на наш взгляд классификация математических моделей, взятая из учебного пособия Л. Э. Хазанова «Моделирование экономических процессов» см. рис. 1 с некоторыми авторскими дополнениями.

Рис. 1.

По возможностям оптимизации процессов или поведения объектов, для которых они разработаны, математические модели бывают оптимизационные и неоптимизационные.

---

Оптимизационные математические модели по числу критериев эффективности делятся на однокритериальные и многокритериальные. Многок­ритериальные математические модели содержат два и более кри­терия.

По учету неизвестных факторов при разработке модели математические модели делят­ся на детерминированные, стохастические и модели с элементами неопределенности.

В стохастических моделях неизвестные факторы — это слу­чайные величины, для которых известны функции распределения и различные статистические характеристики (математическое ожи­дание, дисперсия, среднеквадратическое отклонение и т. п.). Сре­ди стохастических можно выделить:

- модели стохастического программирования, в которых либо в целевую функцию, либо в ограничения входят слу­чайные величины;

- модели теории случайных процессов, предназначенные для изучения процессов, состояние которых в каждый момент време­ни является случайной величиной;

- модели теории массового обслуживания, в которой изучает­ся многоканальные системы, занятые обслуживанием требований. Также к стохастическим моделям можно отнести модели теории полезности, поиска и принятия решений.

Для моделирования ситуаций, зависящих от факторов, для ко­торых невозможно собрать статистические данные и значения ко­торых не определены, используются модели с элементами неоп­ределенности. В моделях теории игр задача представляется в виде игры, в которой участвуют несколько игроков, преследующих раз­ные цели, например организацию предприятия в условиях конку­ренции.

В имитационных моделях реальный процесс разворачивает­ся в машинном времени, и прослеживаются результаты случайных воздействий на него, например организация производственного процесса.

В детерминированных моделях неизвестные факторы не учи­тываются. Несмотря на кажущуюся простоту этих моделей, к ним сводятся многие практические задачи, в том числе большинство экономических задач. По виду целевой функции и ограничений детерминированные модели делятся на линейные, нелинейные, динамические и графические. Для подбора модели оптимизации рациона больных сахарным диабетом более детально рассмотрим детерминированные математические модели, т.к. будем полагать, что на процесс формирования меню больного сахарным диабетом случайные факторы не будет оказывать влияния. Действительно, набор продуктов для приготовления блюд определяется больным, он является неслучайным, блюда, которые можно приготовить из заданных компонентов, выбираются в соответствии с рецептами, хранящимися в базе данных. На этот процесс также случайные факторы или прочие неопределённости не оказывают влияния. Далее должен выполняться расчёт калорийности блюд, их гикемического индекса и показателя, равного количеству хлебных единиц в них. Калорийность, гликемический индекс и показатель наличия углеводов в пище - хлебные единицы являются линейными функциями для блюд по отношению к исходным компонентам, из которых они приготавливаются.

---

В линейных моделях целевая функция и ограничения линей­ны по управляющим переменным. Построение и расчет линейных моделей являются наиболее развитым разделом математического моделирования, поэтому часто к ним стараются свести и другие задачи либо на этапе постановки, либо в процессе решения.

В общем виде задача линейного программирования ставится следующим образом.

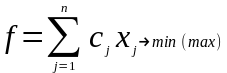(2.1)

при ограничениях:

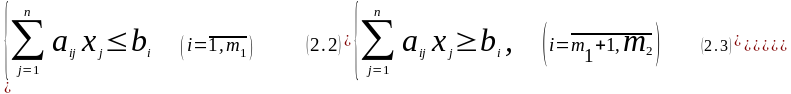
где x_i, j=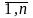 - управляющие переменные или решения задачи (2.1)-(2.4),

b_i, а_ij, i=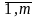 , j=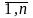 - параметры,

f - целевая функция или критерий эффективности задачи.

Функция (2.1) – линейная, ограниченная (2.2)-(2.4) - линейные. В данной формулировке задача линейного программирования содержит n переменных и m ограничений.

Решить задачу линейного программирования – это значит найти значения управляющих переменных x_i, j=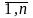 , удовлетворяющих ограничениями (2.2)-(2.4), при которых целевая функция (2.1) принимает минимальное или максимальное значение.

В зависимости от вида целевой функции (2.1) и ограничений (2.2)-(2.4) можно выделить несколько типов задач линейного программирования или линейных моделей: общая линейная задача, транспортная задача, задача о назначениях.

Задача о диете – одна из исторически наиболее ранних сформулированных прикладных задач. Задача о диете возникает при составлении наиболее экономного (т.е. наиболее дешевого) рациона питания животных, удовлетворяющего определенным медицинским требованиям.

Предположим, что в нашем распоряжении имеется n продуктов питания (сено, зерно, комбикорм, соль и т.д.). Обозначим эти продукты через 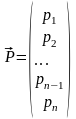. Предположим, что  есть стоимость единицы веса (например, стоимость одного килограмма) продукта .

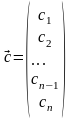Рациональная диета должна доставлять животному определенные компоненты (белки, жиры, углеводы, витамины, микроэлементы и т.д.). Обозначим эти компоненты через 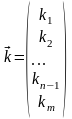 . Тогда можно составить таблицу - справочник см. табл. 2.1, указывающую, какое количество каждого компонента имеется в единице веса каждого продукта.

Таблица 2.1

Продукты Компоненты	Р1	Р2	Р3	….	Рn-1	Pn
k1	a11	a12	a13	….	a1n-1	an
k2	a21	a22	a23	….	a2n-1	a2n
…..	….	….	….	….	….	….
km-1	am-11	am-12	am-13	….	am-1n-1	am-1n
km	am1	am2	am3	….	amn-1	amn

Таким образом, величина a_ij есть количество i-го компонента, содержащегося в единице веса j-го продукта. Матрица 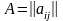 ,  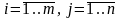называется матрицей питательности.

Рацион кормления должен указать, какое количество х_i i-го продукта должно быть скормлено животному за определенный срок (скажем, за месяц). Он означает, что за этот срок животное должно получить единиц первого продукта x₁, единиц второго продукта – х₂, ….., единиц n-го продукта – х_n.

---

Рассмотрим, какие требования предъявляются к рациону. Во-первых, должны быть выполнены определенные медицинские требования, которые заключаются в том, что за указанный срок животное должно получить не менее определенного количества каждого компонента (не менее определенного количества белков, жиров, витаминов и т.д.). Обозначим через b_j то минимальное количество j-го компонента, которое должно получить животное. Тогда рацион кормления должен удовлетворять ограничениям:

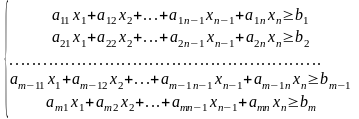  (2.5)

Кроме того очевидно, что все переменные x_i неотрицательны, т.е. x₁0, x₂0,  ... x_n0 (2.6).

Пусть стоимость единицы веса i-го продукта равна с_i. Тогда весь наш рацион будет стоить: с₁х₁ + с₂х₂ + …..+ с_n-1x_n-1 + c_nx_n.

Целесообразно понести минимальные затраты на содержание животных. Поэтому задача о рациональном кормлении животных приобретает вид: найти рацион минимальной стоимости 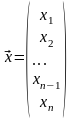при выполнении медицинских ограничений (2.5) и естественных ограничений (2.6). Математически формулировка задачи выглядит следующим образом:

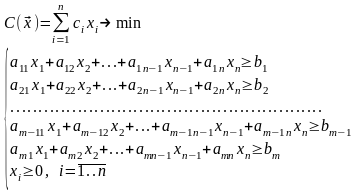(2.7)

Для решения задач линейного программирования общего вида, в том числе и сформулированной выше, можно использовать:

- графический метод (для решения задач размерностью не более 3),

- симплекс-метод,

- современные пакеты прикладных программ – Mathcad, пакет «Поиск решения» табличного процессора MS Excel и другие.

Реальные линейные модели, как правило, имеют размерность гораздо более 3, поэтому для их решения на практике применяют современные прикладные программы, выполняющиеся на ПЭВМ. Это позволяет сократить время нахождения решения и повысить точность получаемых результатов.

Нелинейные модели — это модели, в которых либо целевая фун­кция, либо какое-нибудь из ограничений (либо все ограничения) нелинейны по управляющим переменным. Для нелинейных моде­лей нет единого метода расчета. В зависимости от вида нелиней­ности, свойств функции и ограничений можно предложить различ­ные способы решения. Однако может случиться и так, что для поставленной нелинейной задачи вообще не существует метода решения.

В общем виде задача нелинейного программирования формулируется следующим образом:

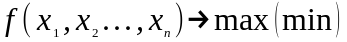
при ограничениях:

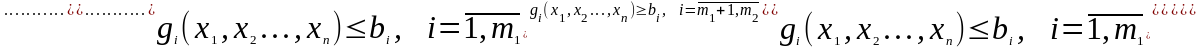(2.8)

где х_j – управляющие переменные или решения задачи нелинейного программирования, ,

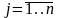b_i – фиксированные параметры, ,

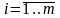f, g_i, 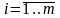- заданные нелинейные функции n переменных.

В динамических моделях в отличие от статических линейных и нелинейных моделей учитывается фактор времени. Критерий оптимальности в динамических моделях может быть самого обще­го вида (и даже вообще не быть функцией), однако для него долж­ны выполняться определенные свойства. Расчет динамических моделей сложен, и для каждой конкретной задачи необходимо раз­рабатывать специальный алгоритм решения.

---

Смотрите также файлы

• 3.3. Дополнение к классификации видов моделирования систем.docx

• 3.2. Классификация видов моделирования систем.docx

• 3.1. Классификация видов моделирования систем и моделей.doc

• 2.4. Принципы и структура системного анализа.docx

• 2.3. Термины и определения системного анализа и теории систем.docx