ВУЗ: Смоленский областной казачий институт промышленных технологий и бизнеса
Категория: Лекция
Дисциплина: Моделирование систем
Добавлен: 19.11.2018
Просмотров: 818
Скачиваний: 8
Для облегчения процесса моделирования используют классификацию СМО по различным признакам, для которых пригодны определенные группы методов и моделей теории массового обслуживания, упрощающие подбор адекватных математических моделей к решению задач обслуживания в коммерческой деятельности.
СМО с ожиданием —
в общем случае многоканальная система
в которую поступает поток заявок с
интенсивностью λ; интенсивность
обслуживания μ
(т. е. в среднем
непрерывно занятый канал будет выдавать
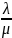 обслуженных заявок в единицу (времени).
Заявка, поступившая в момент, когда
канал занят, становится в очередь и
ожидает обслуживания.
обслуженных заявок в единицу (времени).
Заявка, поступившая в момент, когда
канал занят, становится в очередь и
ожидает обслуживания.
Система с ограниченной длиной очереди. Предположим сначала, что количество мест в очереди ограничено числом m, т. е. если заявка пришла в момент, когда в очереди уже стоят m заявок, она покидает систему необслуженной. В дальнейшем, устремив m к бесконечности, мы получим характеристики одноканальной СМО без ограничений длины очереди.
Будем нумеровать состояния СМО по числу заявок, находящихся в системе (как обслуживаемых, так и ожидающих обслуживания):
 —канал
свободен;
—канал
свободен;
 —канал
занят, очереди нет;
—канал
занят, очереди нет;
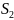 —
канал занят, одна
заявка стоит в очереди;
—
канал занят, одна
заявка стоит в очереди;
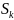 —канал
занят, k - 1 заявок стоят в очереди;
—канал
занят, k - 1 заявок стоят в очереди;
 —
канал занят, k
заявок стоят в очереди.
—
канал занят, k
заявок стоят в очереди.
Граф системы показан на рис. 1.2. Все интенсивности потоков событий, переводящих в систему по стрелкам слева направо, равны λ, а справа налево —μ. Действительно, по стрелкам слева направо систему переводит поток заявок (как только придет заявка, система переходит в следующее состояние), справа же налево — поток «освобождений» занятого канала, имеющий интенсивность μ (как только будет обслужена очередная заявка, канал либо освободится, либо уменьшится число заявок в очереди).
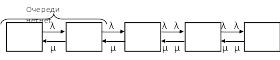
Рис. 1.2. Одноканальная СМО с ожиданием
Изображенная на рис. 1.2 схема представляет собой схему размножения и гибели. Используя общее решение (1.1)—(1. 4), напишем выражения для предельных вероятностей состояний:
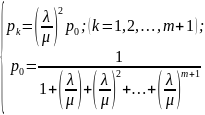 (1.1)
(1.1)
или с использованием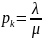 :
:
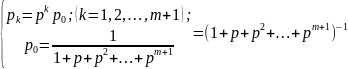 (1.2)
(1.2)
Последняя строка в (1.2) содержит геометрическую прогрессию с первым членом 1 и знаменателем р; откуда получаем:
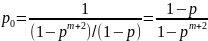 (1.3)
(1.3)
в связи с чем предельные вероятности принимают вид:
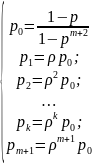 (1.4)
(1.4)
Выражение (1.4)
справедливо только при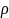 <
1 (при
<
1 (при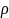 = 1 она дает неопределенность вида 0/0).
Сумма геометрической прогрессии со
знаменателем
= 1 она дает неопределенность вида 0/0).
Сумма геометрической прогрессии со
знаменателем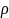 = 1 равна m + 2, и в этом случае
= 1 равна m + 2, и в этом случае

Определим
характеристики СМО: вероятность отказа ,
относительную пропускную способность
q, абсолютную пропускную способность
А, среднюю длину очереди
,
относительную пропускную способность
q, абсолютную пропускную способность
А, среднюю длину очереди ,
среднее число заявок, связанных с
системой
,
среднее число заявок, связанных с
системой
 ,среднее
время ожидания в очереди
,среднее
время ожидания в очереди
 ,
среднее время пребывания заявки в СМО
,
среднее время пребывания заявки в СМО
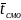 .
.
Вероятность отказа. Очевидно, заявка получает отказ только в случае, когда канал занят и все т мест в очереди тоже:
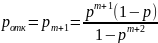 (1.5)
(1.5)
Относительная пропускная способность:
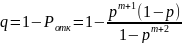 (1.6)
(1.6)
Абсолютная пропускная способность:
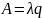
Средняя длина
очереди. Найдем среднее число заявок,
находящихся в очереди, как математическое
ожидание дискретной случайной величины
R — числа заявок, находящихся в очереди:
заявок,
находящихся в очереди, как математическое
ожидание дискретной случайной величины
R — числа заявок, находящихся в очереди:
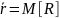
С вероятностью в
очереди стоит одна заявка, с вероятностью
в
очереди стоит одна заявка, с вероятностью —
две заявки, вообще с вероятностью
—
две заявки, вообще с вероятностью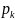 в
очереди стоят k - 1 заявок, и т. д., откуда:
в
очереди стоят k - 1 заявок, и т. д., откуда:
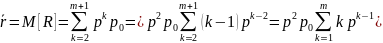 (1.7)
(1.7)
Поскольку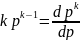 ,
сумму в (1.7) можно трактовать как
производную по
,
сумму в (1.7) можно трактовать как
производную по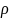 от
суммы геометрической прогрессии:
от
суммы геометрической прогрессии:
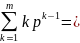
Подставляя данное
выражение в (1.7) и используя из
(1.4), окончательно получаем:
из
(1.4), окончательно получаем:
 (1.8)
(1.8)
Среднее число
заявок, находящихся в системе. Получим
далее формулу для среднего числа
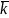 заявок, связанных с системой (как стоящих
в очереди, так и находящихся на
обслуживании). Поскольку
заявок, связанных с системой (как стоящих
в очереди, так и находящихся на
обслуживании). Поскольку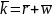 ,
где
,
где —
среднее число заявок, находящихся под
обслуживанием, а k известно, то остается
определить
—
среднее число заявок, находящихся под
обслуживанием, а k известно, то остается
определить .
Поскольку канал один, число обслуживаемых
заявок может равняться 0 (с вероятностью
.
Поскольку канал один, число обслуживаемых
заявок может равняться 0 (с вероятностью )
или 1 (с вероятностью 1 -
)
или 1 (с вероятностью 1 - ),
откуда:
),
откуда:
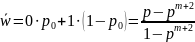
и среднее число заявок, связанных с СМО, равно
 (1.9)
(1.9)
Среднее время
ожидания заявки в очереди. Обозначим
его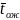 ;
если заявка приходит в систему в какой-то
момент времени, то с вероятностью
;
если заявка приходит в систему в какой-то
момент времени, то с вероятностью канал
обслуживания не будет занят, и ей не
придется стоять в очереди (время ожидания
равно нулю). С вероятностью
канал
обслуживания не будет занят, и ей не
придется стоять в очереди (время ожидания
равно нулю). С вероятностью она
придет в систему во время обслуживания
какой-то заявки, но перед ней не будет
очереди, и заявка будет ждать начала
своего обслуживания в течение
времени
она
придет в систему во время обслуживания
какой-то заявки, но перед ней не будет
очереди, и заявка будет ждать начала
своего обслуживания в течение
времени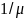 (среднее
время обслуживания одной заявки). С
вероятностью
(среднее
время обслуживания одной заявки). С
вероятностью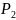 в
очереди перед рассматриваемой заявкой
будет стоять еще одна, и время ожидания
в среднем будет равно
в
очереди перед рассматриваемой заявкой
будет стоять еще одна, и время ожидания
в среднем будет равно ,
и т. д.
,
и т. д.
Если же k = m + 1, т.
е. когда вновь приходящая заявка застает
канал обслуживания занятым и m заявок
в очереди (вероятность этого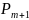 ),
то в этом случае заявка не становится
в очередь (и не обслуживается), поэтому
время ожидания равно нулю. Среднее время
ожидания будет равно:
),
то в этом случае заявка не становится
в очередь (и не обслуживается), поэтому
время ожидания равно нулю. Среднее время
ожидания будет равно:

если подставить сюда выражения для вероятностей (1.4), получим:
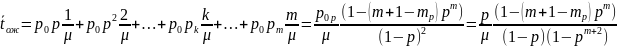 (1.10)
(1.10)
Здесь использованы
соотношения (1.7), (1.10) (производная
геометрической прогрессии), а также из
(1.4). Сравнивая это выражение с (1.10),
замечаем, что иначе говоря, среднее
время ожидания равно среднему числу
заявок в очереди, деленному на интенсивность
потока заявок.
из
(1.4). Сравнивая это выражение с (1.10),
замечаем, что иначе говоря, среднее
время ожидания равно среднему числу
заявок в очереди, деленному на интенсивность
потока заявок.
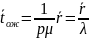 (1.11)
(1.11)
Среднее время
пребывания заявки в системе.
Обозначим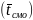 матожидание
случайной величины — время пребывания
заявки в СМО, которое складывается из
среднего времени ожидания в очереди
матожидание
случайной величины — время пребывания
заявки в СМО, которое складывается из
среднего времени ожидания в очереди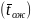 и
среднего времени обслуживания
и
среднего времени обслуживания .
Если загрузка системы составляет 100 %,
очевидно,
.
Если загрузка системы составляет 100 %,
очевидно, , в противном же случае
, в противном же случае

Отсюда