Файл: 9.1. Постановка и методы решения задач стохастического программирования.doc
ВУЗ: Смоленский областной казачий институт промышленных технологий и бизнеса
Категория: Лекция
Дисциплина: Моделирование систем
Добавлен: 19.11.2018
Просмотров: 3101
Скачиваний: 71
СОДЕРЖАНИЕ
10. Стохастическое программирование
10.1. Понятие о стохастическом программировании
10.4. Примеры задач стохастического программирования
10.4.1. Задача планирования добычи угля в априорных решающих правилах
10.4.2. Стохастическая транспортная задача
10.5. Задачи с построчными вероятностными ограничениями
10.6. Одноэтапные стохастические задачи с линейными решающими правилами
10. Стохастическое программирование
10.1. Понятие о стохастическом программировании
В моделях математического программирования некоторые или все параметры, показатели качества и ограничения могут оказаться неопределенными или случайными.
Стохастическое программирование (СП) – раздел математики, занимающийся условными экстремальными задачами, в которых параметры условий или составляющие решений являются случайными.
Случаи, когда опыт, статистика или исследование процесса позволяют устанавливать вероятностные характеристики задач, называются ситуациями, связанными с риском.
Случаи, когда неизвестны статистические особенности процесса, называются неопределенными ситуациями.
Стохастическое программирование используется для решения задач двух типов.
1. В задачах первого типа прогнозируются статистические характеристики множества одинаковых экстремальных систем. Это задачи пассивного СП.
2. В задачах второго типа строятся алгоритмы планирования и управления в условиях неполной информации. Это задачи активного СП.
В зависимости от постановки задачи стохастического программирования её решения или планы могут вычисляться в двух видах:
-
в чистых стратегиях, когда результатом будет вектор оптимального плана или решения задачи. Решения в чистых стратегиях называются решающими правилами;
-
в смешанных стратегиях, когда определяется вероятностное распределение компонент оптимального плана или решения, которые в этом случае называются решающими распределениями.
При построении моделей управления в условиях неполной информации существует два подхода к использованию информации:
-
в первом случае решение предшествует наблюдению, тогда решающие правила и решающие распределения зависят только от детерминированных параметров и статистических характеристик случайных параметров условий задачи, т. е. являются априорной информацией,
-
во втором случае наблюдения предшествуют решению, тогда решающие правила и решающие распределения определяются апостериорной информацией, появляющейся в результате наблюдения за конкретной реализацией параметров условий задачи.
Решающие распределения представляют собой функции, таблицы или инструкции, устанавливающие зависимость решения от некоторой априорной или апостериорной информации.
10.2. Постановка задач СП
Большое число военных, экономических, технических задач записывается в виде задачи ЛП:
![]()
В конкретных случаях коэффициенты Cj, aij, bi могут быть случайными величинами. Простая замена случайных параметров их усредненными характеристиками не всегда возможна по двум причинам:
-
может исказиться модель самой исследуемой операции и не отражать реальных условий;
-
решение усредненной задачи может при конкретных реализациях не удовлетворять ограничениям.
Задачи СП могут формулироваться в трех видах
1. Формулировка задачи, при которой требуется соблюдение ограничений при всех реализациях случайных параметров и любое их нарушение приводит к таким большим штрафам, что сводит на нет эффект от оптимизации целевой функции, называется жесткой постановкой.
Жесткая постановка задачи требует расширения гиперплоскостей ограничений, и в результате ОДР может оказаться вырожденной, а сама задача потеряет смысл. Таким образом, замена случайных параметров их средними значениями при жесткой постановке не всегда приводит к правильному решению задачи СП.
2. Во многих задачах нет необходимости удовлетворять ограничениям при каждой реализации случайного изменения параметра.
Если в конкретной задаче требуется только чтобы вероятность попадания решения в допустимую область превышала некоторое заранее заданное число >0 (обычно >1/2), то такая постановка задач СП называется моделью с вероятностными ограничениями.
Если коэффициент cj детерминирован, то целевая функция задачи с вероятностными ограничениями не изменяется. Если сj случайно, то в качестве целевой функции задачи с вероятностными ограничениями берут математическое ожидание целевой функции
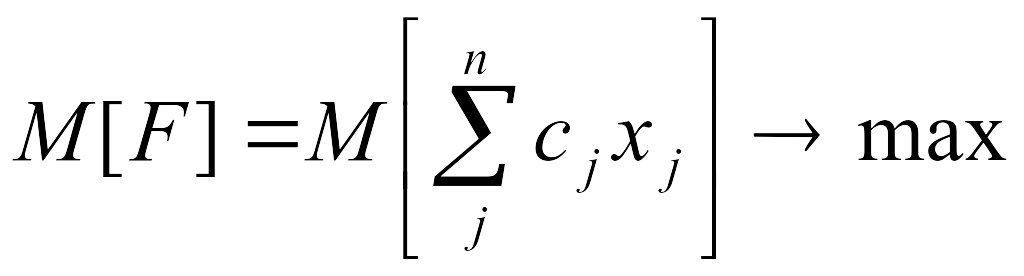 (10.1)
(10.1)
или вероятность превышения целевой функции некоторого фиксированного порога F0 :
P(F>F0).
В некоторых задачах её условия позволяют заменить ограничения со случайными параметрами неравенствами, ограничивающими первые или вторые моменты распределения левых частей условий:
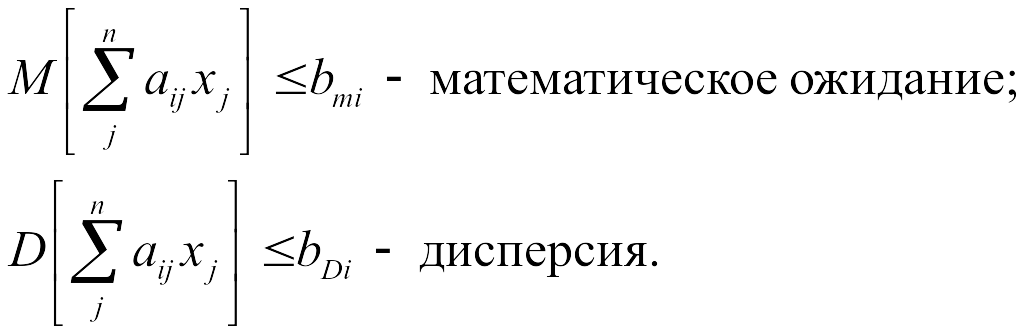
(10.2)
(10.3)
3. Если ограничения представляют собой не просто вторые моменты распределения условий, а вторые моменты некоторых функций S от невязок условий
![]()
![]() (10.4)
(10.4)
такая постановка задач СП называется моделью со статистическими условиями.
В этом случае невязки в ограничениях задач со статистическими условиями исключены не во всех случаях (как в жесткой постановке) и не в большинстве случаев (как в задачах с вероятностными ограничениями), а в среднем, т. е. средняя величина невязки условий равна нулю.
Если в задачах присутствуют как вероятностные, так и статистические и жесткие условия, такие модели называются моделями со смешанными условиями.
10.3. Модели задач СП
Задачи СП различаются по трем признакам.
1. По характеру решений (детерминированный или случайный вектор, чистые или смешанные стратегии).
2. По выбору показателя качества, т. е. целевой функции. Если находится:
а) математическое ожидание от целевой функции, т.е.
![]() ,
то такие задачи называются М-моделями;
,
то такие задачи называются М-моделями;
б) если минимизируется дисперсия целевой функции
![]() то
такие задачи называются V-моделями;
то
такие задачи называются V-моделями;
в)
если определяется вероятность превышения
целевой функцией некоторого порога F0,
т. е.
![]() ,
то такие задачи называются Р-моделями.
,
то такие задачи называются Р-моделями.
3. По способу расчленения ограничений задачи могут быть:
а) С построчными вероятностными ограничениями, когда учитываются стохастические связи только в одной строке:
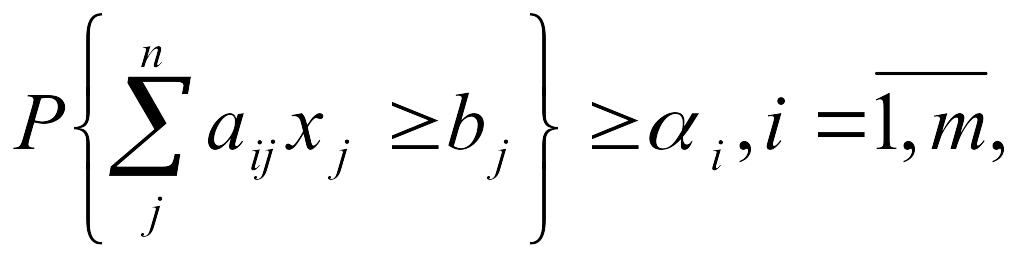
где i - вероятность соблюдения условий,
0i =1 – i вероятность несоблюдения условий.
б) С общими вероятностными ограничениями Р[АХ ≥ В] ≥ , когда могут быть коррелированы параметры не только строки, но и между строками. В такой модели не учитывается сравнительная важность отдельных ограничений.
10.4. Примеры задач стохастического программирования
10.4.1. Задача планирования добычи угля в априорных решающих правилах
В угольной промышленности технико-экономические показатели сильно зависят от природных факторов, которые не всегда могут быть предсказаны заранее. Это:
-
мощность и угол падения пластов,
-
обводнённость участков,
-
склонность к выбрасыванию газов,
-
физико-механические свойства угля и пород,
-
надежность оборудования, эксплуатационные расходы.
Природные условия сказываются на надежности оборудования, эксплуатационных расходах и т. д. и, в конечном счете, на области определения допустимых решений. Поэтому выбор оптимального проекта плана (решения) – это задача стохастического программирования.
Для простоты допускается:
-
показатель плана определяется средним значением суммарных затрат,
-
область определения плана задается спросом на добываемый уголь (требуемый объем добычи) и фондом заработной платы.
Задача планирования угледобычи следующая.
Для i шахты заранее разрабатывается несколько вариантов развития. Требуется установить наиболее рациональный, с точки зрения объединения шахт, вариант развития каждой шахты.
Пусть
![]() ,
если для i
-й шахты принят j-й
вариант, иначе
,
если для i
-й шахты принят j-й
вариант, иначе![]() По каждой шахте реализуется только один
вариант, т.
е.
По каждой шахте реализуется только один
вариант, т.
е.
![]() .
.
![]() -
годовые затраты на добычу угля в i-й
шахте по j-му
варианту при реализации w
случайных параметров, зависящих от
природных факторов.
-
годовые затраты на добычу угля в i-й
шахте по j-му
варианту при реализации w
случайных параметров, зависящих от
природных факторов.
![]() -
годовой объем добычи угля в i-й
шахте по j-му
варианту при реализации w
случайных
природных факторов.
-
годовой объем добычи угля в i-й
шахте по j-му
варианту при реализации w
случайных
природных факторов.
![]() -
годовой фонд зарплаты i
-й шахты по j-му
варианту развития при реализации w
случайных природных факторов.
-
годовой фонд зарплаты i
-й шахты по j-му
варианту развития при реализации w
случайных природных факторов.
d — требуемая в соответствии с планом более высокого уровня годовая добыча угля по объединению в целом.
k - общий фонд зарплаты по объединению.
d ,k - заданные вышестоящей организацией вероятности соблюдения ограничений по обеспечению спроса и по фонду зарплаты соответственно. В этом случае целевая функция соответствует М-модели
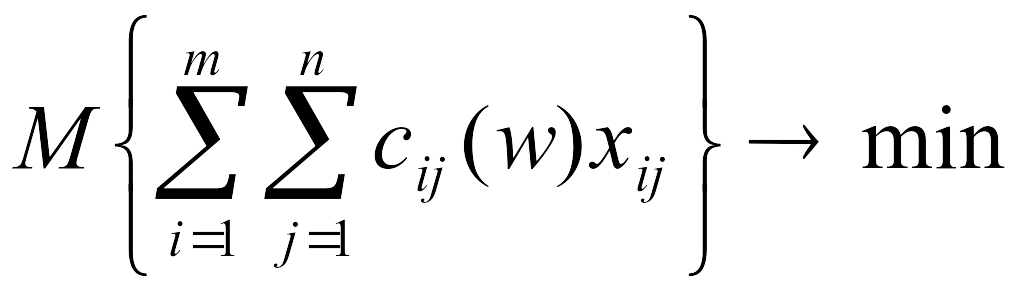 . (10.5)
. (10.5)
Ограничения имеют характер построчных вероятностных ограничений по соблюдению спроса и фонда заработной платы
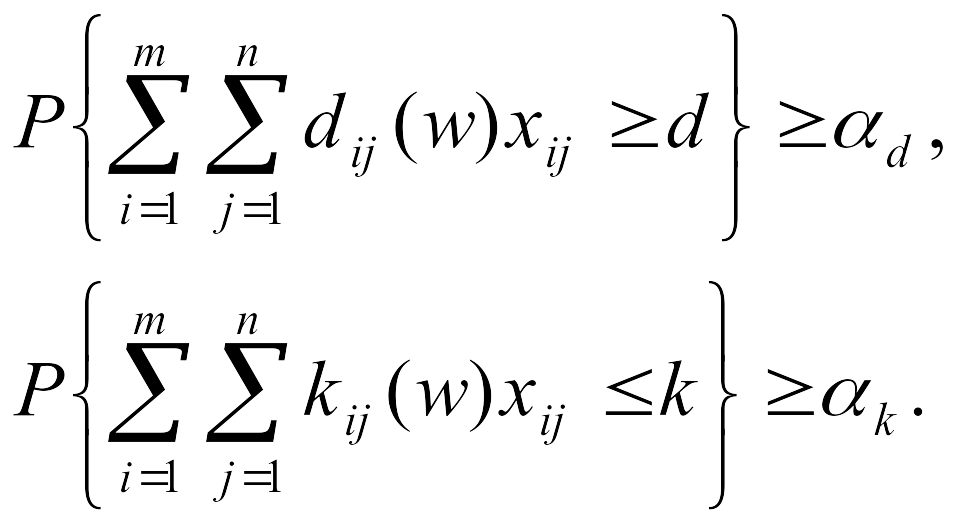
(10.6)
(10.7)
В целом это типичная модель задачи стохастического программирования.
10.4.2. Стохастическая транспортная задача
Обычная транспортная задача имеет целевую функцию и ограничения в виде
![]() .
.
Будем рассматривать задачу при различном характере спроса, который является случайной величиной, т. е. зависит от случайных параметров w,
bj=bj(w) . (10.8)
При этом возможны два варианта формулировки модели задачи.
Вариант
1. Пусть спрос
bj
непрерывно распределен с плотностью
вероятности
![]() .
Примем
.
Примем
![]() – это общий объем продукта, предназначенный
в соответствии с планом, составленным
до реализации bj
(w),
для j-го
пункта потребления.
– это общий объем продукта, предназначенный
в соответствии с планом, составленным
до реализации bj
(w),
для j-го
пункта потребления.
После определения спроса может оказаться, что yj < bj(w), тогда спрос не будет удовлетворен, и ущерб за невыполнение потребности будет пропорционален величине невыполнения с некоторым коэффициентом qj, где qj - штраф за невыполнение заявки за каждую единицу недовезенного продукта. Общий ущерб определяется как
![]() (10.9)
(10.9)
В
случае избытка, аналогично, возрастают
затраты на хранение пропорционально
величине избытка с коэффициентом
![]() (коэффициент штрафа за избыток). Общий
ущерб от избытка при
(коэффициент штрафа за избыток). Общий
ущерб от избытка при
![]() будет
будет
![]() .
(10.10)
.
(10.10)
Математическое ожидание суммарных потерь, связанных с перевозкой продукта, ущерба от неудовлетворенного спроса и затрат на хранение избыточных продуктов определяется следующей целевой функцией
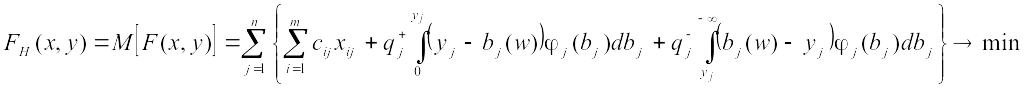 ,
(10.11) где пределы интегрирования очевидны
и определяются на рис. 10.1 избыточным
(1) или недовезенным грузом (2) функции
плотности распределения j
(bj).
,
(10.11) где пределы интегрирования очевидны
и определяются на рис. 10.1 избыточным
(1) или недовезенным грузом (2) функции
плотности распределения j
(bj).
В общем виде целевая функция может быть
представлена как
общем виде целевая функция может быть
представлена как
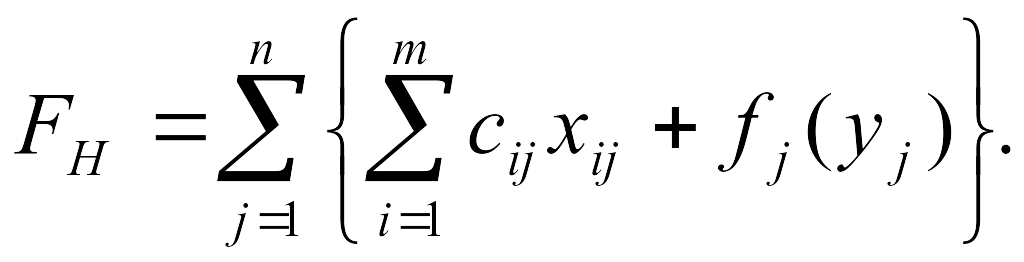 (10.12)
(10.12)
Продифференцируем
![]() дважды по
дважды по
![]() ,
,
![]()
Это
означает, что
![]() ,
а вместе с ней и F
(x,y)
будут функцией, выпуклой вниз относительно
,
а вместе с ней и F
(x,y)
будут функцией, выпуклой вниз относительно
![]() .
.
Таким образом, детерминированный эквивалент стохастической транспортной задачи с непрерывно распределенным спросом представляет собой задачу выпуклого программирования с нелинейной целевой функцией и линейной системой ограничений.
Вариант
2. Пусть спрос
bj(w)
распределен дискретно и в j-м
пункте потребления принимает значения
bik
с вероятностями: pjk
(k=1…s).
Аналогично ранее рассмотренной задаче
![]() ,
,
![]() - коэффициенты
штрафа за дефицит и издержки хранения
единицы продукции.
- коэффициенты
штрафа за дефицит и издержки хранения
единицы продукции.
Введем вспомогательные переменные vjk, иjk - величины избытка и дефицита в j-м пункте потребления при реализации k-го варианта спроса, т.е. при bj(w)=bjk . Целевая функция – математическое ожидание суммарных затрат – будет включать общую стоимость перевозок и штрафы за дефицит и избыток:
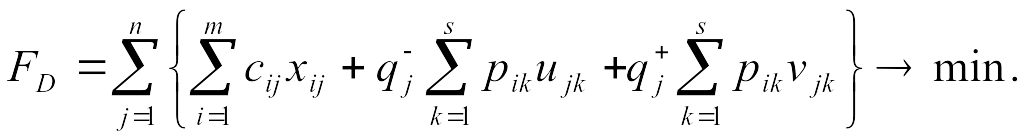 (10.13)
(10.13)
Всегда
имеет место равенство
![]() ,
которое означает, что спрос bjk
удовлетворяется привезенным продуктом
,
которое означает, что спрос bjk
удовлетворяется привезенным продуктом
![]() и
дефицитом иjk
за вычетом
избытка vik.
Подставляя
полученное значение bjk
в целевую функцию после преобразования,
получаем:
и
дефицитом иjk
за вычетом
избытка vik.
Подставляя
полученное значение bjk
в целевую функцию после преобразования,
получаем:
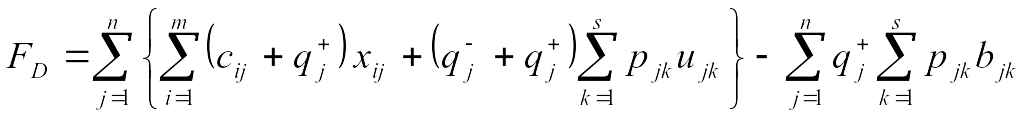 .
(10.14)
.
(10.14)
Второе слагаемое не содержит параметра управления, поэтому формально в модели может не учитываться.
Таким образом, детерминированный эквивалент стохастической транспортной задачи с дискретно распределенным спросом представляется моделью линейного программирования с целевой функцией fd и линейными ограничениями:
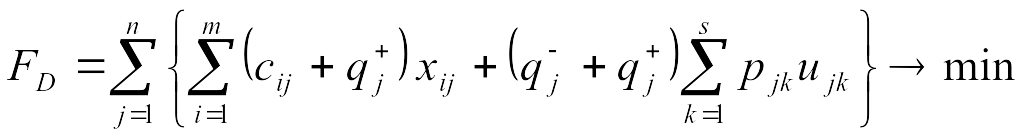 ,
,
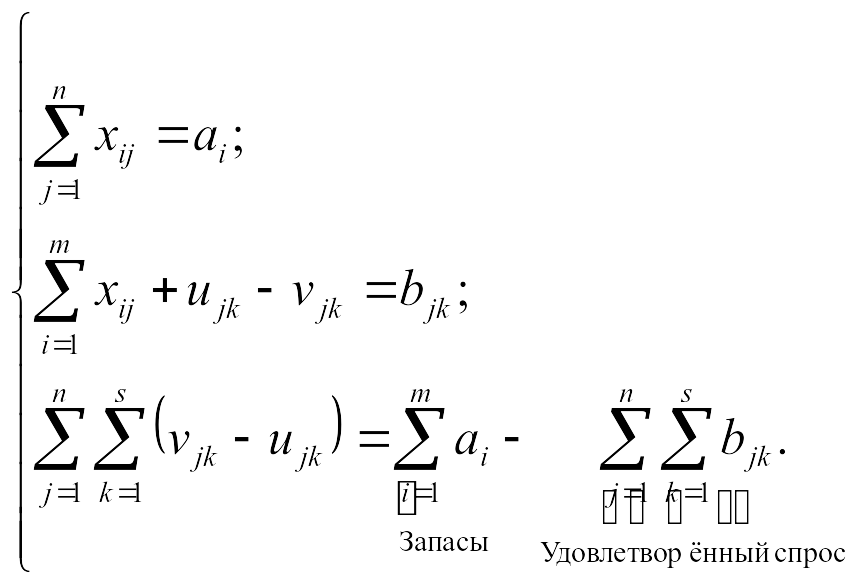
(10.15)
Последнее ограничение означает, что разница между запасами и удовлетворенным спросом определяется дефицитом или избытками.
Аналогично могут быть сформулированы и другие стохастические транспортные задачи, у которых случайным может быть, например, объем производства аi = ai(w).
Эти задачи могут быть также сведены к задачам выпуклого или линейного программирования.
10.5. Задачи с построчными вероятностными ограничениями
Типовая задача стохастического программирования представляет собой М-модель с построчными вероятностными ограничениями и имеет вид:
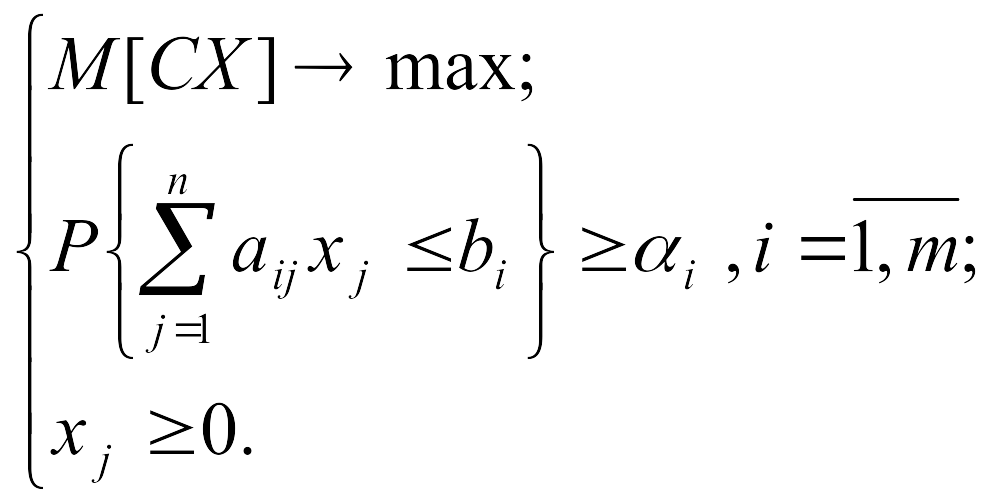 (10.16)
(10.16)
В зависимости от того, какие коэффициенты модели представляют собой случайные величины, выделяется несколько типов задач.
Вариант А. А =||aij|| - детерминированная матрица,
![]() -
случайная матрица-столбец,
-
случайная матрица-столбец,
![]() -
случайные величины.
-
случайные величины.
Считается,
что задана совместная плотность
распределения составляющих bi
случайного
вектора
В:
![]()
Чтобы
определить плотность распределения
одной компоненты, необходимо
проинтегрировать совместную плотность
распределения
![]() по всем параметрам, за исключением
по всем параметрам, за исключением
![]()
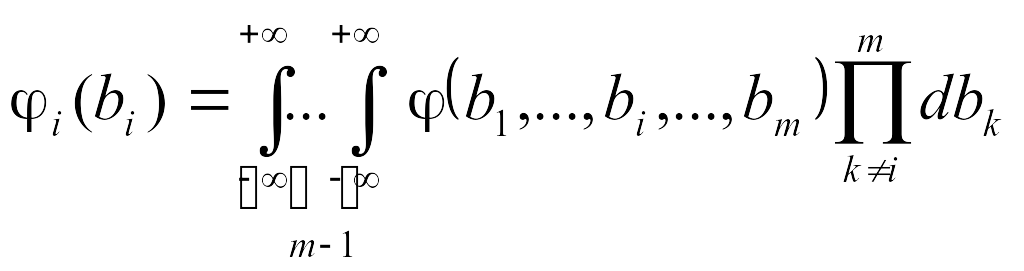 .
.
Зная
распределение одной случайной величины
![]() ,
можно определить значение порога
,
можно определить значение порога
![]() из уравнения
из уравнения
![]() ,
(10.17)
,
(10.17)
где
![]() является нижним пределом интегрирования.
является нижним пределом интегрирования.
Она
определяется как заданная вероятность
i
превышения
случайной величиной bi
порога
![]() ,
что иллюстрируется на рис. 10.2.
,
что иллюстрируется на рис. 10.2.
Следовательно, построчные вероятностные ограничения
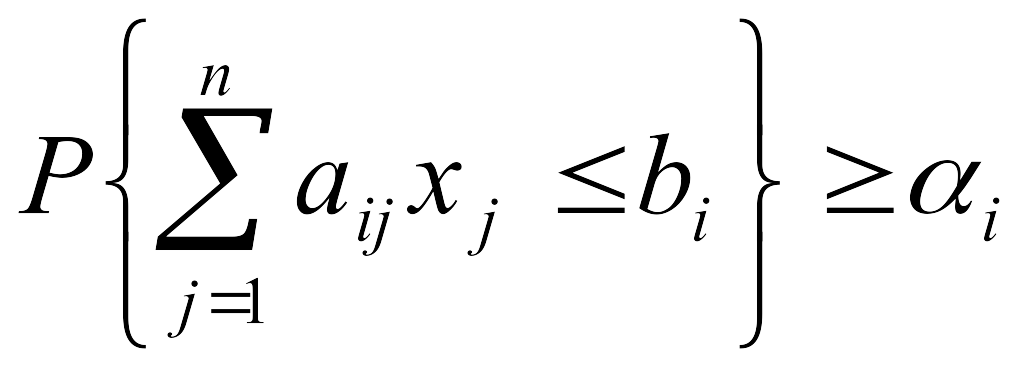 (10.18)
(10.18)
можно записать в виде неравенства
![]() (10.19)
(10.19)
Таким образом, задача для варианта А запишется в матричном виде
![]() (10.20)
(10.20)
где![]() – вычисленные значения порогов для
всех построчных ограничений.
– вычисленные значения порогов для
всех построчных ограничений.
Таким образом, задача при детерминированной матрице А и случайном столбце В будет решаться как детерминированная задача ЛП.
Вариант
В. Принимаются
элементы матрицы А=||аij||
- нормально
распределенные независимые случайные
величины со средним значением
![]() и дисперсией
и дисперсией
![]() .
Составляющие случайного вектора
B=||bj||T
- нормально распределенные независимые
случайные величины со средним значением
.
Составляющие случайного вектора
B=||bj||T
- нормально распределенные независимые
случайные величины со средним значением
![]() и дисперсией
и дисперсией
![]() .
Принимаем, что вероятность соблюдения
построчных ограничений
аi0,5.
.
Принимаем, что вероятность соблюдения
построчных ограничений
аi0,5.
При принятых допущениях невязка i-го вероятностного ограничения из (10.16) будет случайной величиной с нормальным распределением, как линейная комбинация нормально распределенных aij и bi . Таким образом, невязка имеет вид
![]() . (10.21)
. (10.21)
Эта
невязка имеет среднее значение
![]() и
дисперсию
и
дисперсию
![]()
Построчные
вероятностные ограничения можно выразить
через невязку в виде неравенства
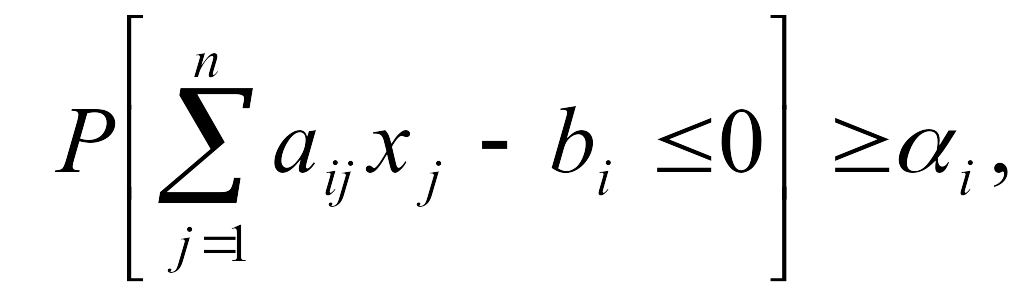 следовательно,
следовательно,
![]() .
Или для нормального распределения
вероятность можно определить по известной
формуле нормального распределения
.
Или для нормального распределения
вероятность можно определить по известной
формуле нормального распределения
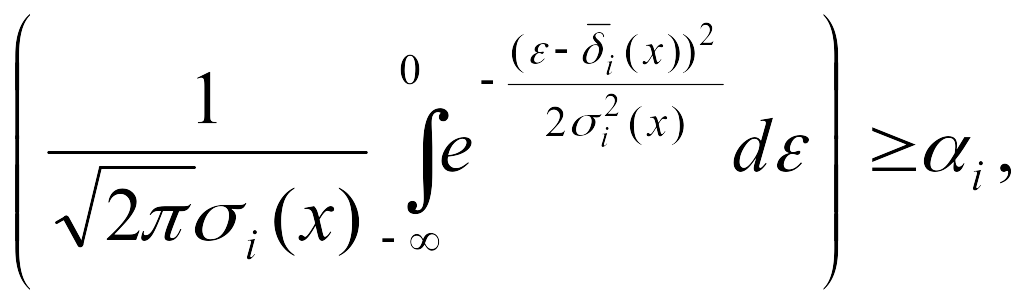 (10.22)
(10.22)
где - параметр интегрирования.
Вводя интеграл вероятности Ф, соотношение (10.22) можно записать в виде
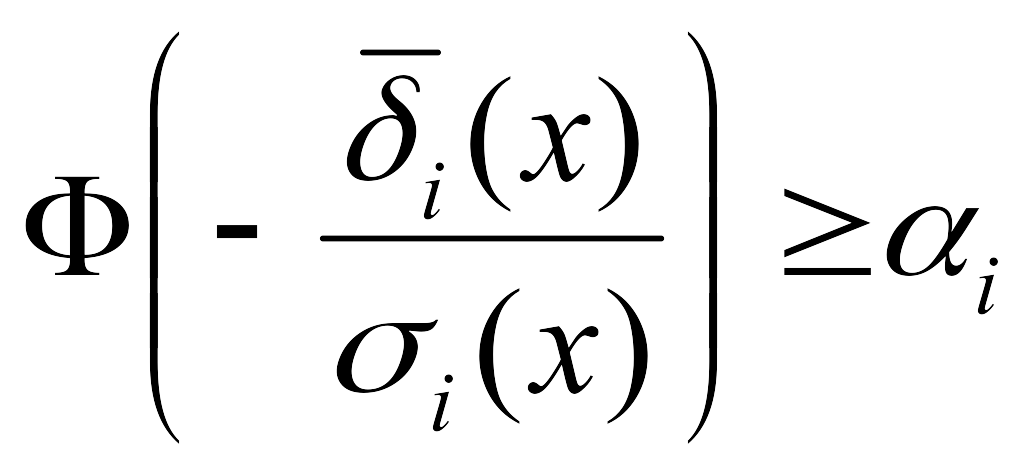 или
или
![]() , (10.23)
, (10.23)
где
![]() -
функция,
обратная интегралу вероятности. Иначе:
-
функция,
обратная интегралу вероятности. Иначе:![]() Подставляя сюда значения
Подставляя сюда значения
![]() ,
,![]() получаем
получаем
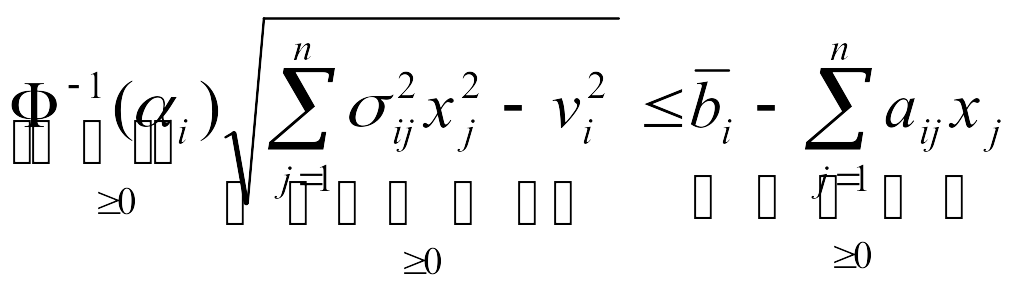 .
(10.24)
.
(10.24)
Ф-1(![]() )0.
Область, ограничиваемая этим соотношением,
выпукла, а сами ограничения квадратичны,
т.к.
)0.
Область, ограничиваемая этим соотношением,
выпукла, а сами ограничения квадратичны,
т.к.
![]() .
.