Файл: 8.1. Постановка задачи динамического программирования. Принцип Беллмана..docx
ВУЗ: Смоленский областной казачий институт промышленных технологий и бизнеса
Категория: Лекция
Дисциплина: Моделирование систем
Добавлен: 19.11.2018
Просмотров: 664
Скачиваний: 12
Динамическое программирование
Динамическое программирование (ДП) – метод оптимизации, приспособленный к операциям, в которых процесс принятия решения может быть разбит на этапы (шаги). Такие операции называются многошаговыми. Начало развития ДП относится к 50-м годам ХХ в. Оно связано с именем американского математика Р. Беллмана.
Если модели линейного программирования можно использовать в экономике для принятия крупномасштабных плановых решений в сложных ситуациях, то модели ДП применяются при решении задач значительно меньшего масштаба, например, при разработке правил управления запасами, устанавливающими момент пополнения запасов и размер пополняющего заказа; при разработке принципов календарного планирования производства и выравнивания занятости в условиях колеблющегося спроса на продукцию; при распределении дефицитных капитальных вложений между возможными новыми направлениями их использования при составлении календарных планов текущего и капитального ремонта сложного оборудования и его замены; при разработке долгосрочных правил замены выбывающих из эксплуатации основных фондов и т.п.
В реально функционирующих больших экономических системах еженедельно требуется принимать микроэкономические решения. Модели ДП ценны тем, что позволяют на основе стандартного подхода с использованием при минимальном вмешательстве человека принимать такие решения. И если каждое взятое в отдельности такое решение малосущественно, то в совокупности эти решения могут оказать большое влияние на прибыль.
Приведем общую постановку задачи ДП. Рассматривается управляемый процесс, например, экономический процесс распределения средств между предприятиями, ресурсов в течение ряда лет, замены оборудования, пополнения запасов и т.п. В результате управления система (объект управления) S переводится из начального состояния s0 в состояние S.
Предположим, что управление можно разбить на п шагов, т.е. решение принимается последовательно на каждом шаге, а управление, переводящее систему S из начального состояния в конечное, представляет собой совокупность п пошаговых управлений.
Обозначим через Хk управление на k-м шаге (k=1, 2, ..., п). Переменные Хk удовлетворяют некоторым ограничениям и в этом смысле называются допустимыми (Хk может быть числом, точкой в п-мерном пространстве, качественным признаком).
Пусть Х (Х1, Х1, ..., Хn) – управление, переводящее систему S из состояния s0 в состояние sn Обозначим через sk состояние системы после k-го шага управления. Получаем последовательность состояний s0, s1,..., sk-1, sk,..., sn-1, sn=Sm, которую изобразим кружками (рис. 1.1).

Рис.1.1.
Показатель эффективности рассматриваемой управляемой операции – целевая функция – зависит от начального состояния и управления:
Z=F(s0,Х) (1.1)
Сделаем несколько предположений.
1. Состояние sk системы в конце k-го шага зависит только предшествующего состояния sk-1 и управления на k-м шаге Хk. (и не зависит от предшествующих состояний и управлений). Это требование называется «отсутствием последействия». Сформулированное положение записывается в виде уравнений:
sk=k(sk-1,Хk),k=1,2,…,n,
(1.2)
которые называются
уравнениями состояний.
2. Целевая функция (1) является аддитивной от показателя эффективности каждого шага. Обозначим показатель эффективности k-го шага через
Zk=fk(sk-1,Хk),k=1,2,…,n, (1.3)
Тогда
Z=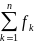 (sk-1,Хk).
(1.4)
(sk-1,Хk).
(1.4)
Задача пошаговой оптимизации
(задача ДП) формулируется так: определить
такое допустимое управление Х, переводящее
систему S из состояния s0
всостояние 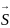 ,
при котором целевая функция (1.4) принимает
наибольшее(наименьшее) значение.
,
при котором целевая функция (1.4) принимает
наибольшее(наименьшее) значение.
Выделим особенности модели ДП:
1. Задача оптимизации интерпретируется как п-шаговый процесс управления
2. Целевая функция равна сумме
целевых функций каждого шага.
З.
Выбор управления на k-м
шаге зависит только от состояния системы
к этому шагу, не влияет на предшествующие
шаги (нет обратной связи).
4.
Состояние sk после k-го
шага управления зависит только от
предшествующего состояния sk-1
и управления Хk (отсутствие
последействия).
5.
На каждом шаге управление Хk
зависит от конечного числа управляющих
переменных, а состояние sk
– от конечного числа параметров.
Смысл замечаний станет ясным из рассмотренных ниже примеров. Существуют различные способы решения подобных задач, применяемые в зависимости от вида функций, ограничений, размерности и т. п. Рассмотрим вычислительную схему ДП, которая окажется безразличной к способам задания функций и ограничений. Вычислительная схема связана с принципом оптимальности и использует рекуррентные соотношения.
Принцип оптимальности впервые был сформулирован Р. Беллманом в 1953г. Каково бы ни было состояние S системы в результате какого-либо числа шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая данный.
Беллманом были сформулированы и условия, при которых принцип верен. Основное требование – процесс управления должен быть без обратной связи, т.е. управление на данном шаге не должно оказывать влияния на предшествующие шаги.
Принцип оптимальности утверждает, что для любого процесса без обратной связи оптимальное управление таково, что оно является оптимальным для любого подпроцесса по отношению к исходному состоянию этого подпроцесса. Поэтому решение на каждом шаге оказывается наилучшим с точки зрения управления в целом. Если изобразить геометрически оптимальную траекторию в виде ломаной линии, то любая часть этой ломаной будет являться оптимальной траекторией относительно начала и конца.
Уравнения Беллмана. Вместо исходной задачи ДП с фиксированным числом шагов п и начальным состоянием s0 рассмотрим последовательность задач, полагая последовательно п=1, 2, ... при различных s – одношаговую, двухшаговую и т.д., – используя принцип оптимальности.
Рассмотрим пример применения
метода динамического программирования
к задаче, которую можно интерпретировать
как задачу распределения ресурсов между
технологическими процессами. Имеется
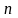 технологических процессов, по которым
надо распределить однородный ресурс
(например деньги, или рабочую силу, или
энергию) так, чтобы максимизировать
общий доход. Пусть использование в i-м
технологическом процессе ресурса в
количестве
технологических процессов, по которым
надо распределить однородный ресурс
(например деньги, или рабочую силу, или
энергию) так, чтобы максимизировать
общий доход. Пусть использование в i-м
технологическом процессе ресурса в
количестве
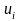 приносит доход
приносит доход
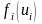 ,
а общее количество ресурса равняется
,
а общее количество ресурса равняется
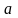 .
Тогда задача состоит в максимизации
функции:
.
Тогда задача состоит в максимизации
функции:
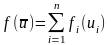 ,
,
при
ограничении
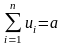 .
.
Рассмотрим наряду с этой
задачей класс аналогичных задач, в
которых может меняться число процессов
и общее количество ресурсов. Обозначим
оптимальное значение в задаче с
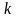 процессами и количеством ресурсов
процессами и количеством ресурсов
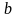 через
через
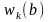 ,
тогда в исходной задаче оптимальное
значение равно
,
тогда в исходной задаче оптимальное
значение равно
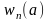 .
Для поставленных задач справедлив
принцип оптимальности, который здесь
можно сформулировать следующим образом:
если для всех процессов в задаче ресурс
распределен оптимально, то для части
процессов доля ресурса, приходящаяся
на них при таком
распределении, также должна быть
распределена оптимально. Если этот
принцип применить к задаче с
.
Для поставленных задач справедлив
принцип оптимальности, который здесь
можно сформулировать следующим образом:
если для всех процессов в задаче ресурс
распределен оптимально, то для части
процессов доля ресурса, приходящаяся
на них при таком
распределении, также должна быть
распределена оптимально. Если этот
принцип применить к задаче с
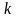 процессами и количеством ресурсов
процессами и количеством ресурсов
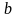 и предположить, что в k-й
процесс вкладывается количество ресурса
и предположить, что в k-й
процесс вкладывается количество ресурса
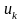 ,
то получаем формулу:
,
то получаем формулу:
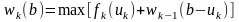 ,
,
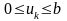
Эта формула справедлива при
любых
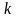 и
и
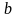 ,
поэтому для исходной задачи имеем
цепочку соотношений:
,
поэтому для исходной задачи имеем
цепочку соотношений:
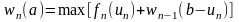 ,
,
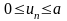
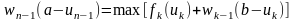 ,
,
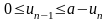
и т.д. Для первого процесса, когда ресурсы по остальным процессам уже распределены, получаем:
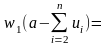
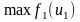 ,
,
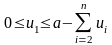
С помощью таких рекуррентных
соотношений можно решить задачу
оптимального распределения ресурсов.
Рассмотрим конкретный пример с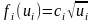 .Итак,
требуется максимизировать:
.Итак,
требуется максимизировать:
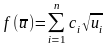 при ограничении
при ограничении
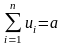 .Имеем
.Имеем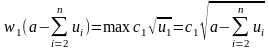 ,
,
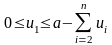 , а
условно оптимальное использование
ресурса в первом процессе есть
, а
условно оптимальное использование
ресурса в первом процессе есть
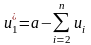 .
.
Далее,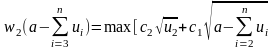 ,
,
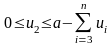
Дифференцируя выражение в
квадратных скобках по
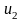 и приравнивая производную к нулю,
получаем соотношение
и приравнивая производную к нулю,
получаем соотношение
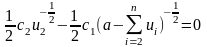 ,
,
откуда
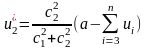 ,
,
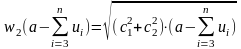 .
.
На следующем шаге
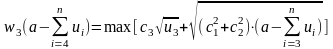 ,
,
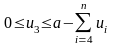 .
.
Решая эту задачу максимизации, как и на предыдущем шаге, получаем
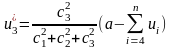 ,
,
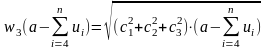 .
.
Продолжая вычисления по
процедуре, получаем общие выражения
для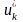 и
и
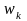 :
:
 ,
,
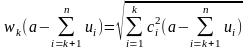 .
.
Так как для последнего
технологического процесса должно
выполняться ограничение
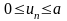 ,
то на n-м шаге находим
просто оптимальное значение задачи
,
то на n-м шаге находим
просто оптимальное значение задачи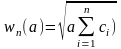 .
.
и оптимальное использование
ресурса в n-м процессе
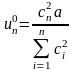 .
.
Подставляя
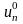 в выражение для
в выражение для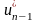 ,
затем в
,
затем в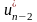 и т.д., получаем решение задачи
и т.д., получаем решение задачи
 .
.