Файл: Задача стохастического программирования для самостоятельного решения.docx
ВУЗ: Смоленский областной казачий институт промышленных технологий и бизнеса
Категория: Задание
Дисциплина: Моделирование систем
Добавлен: 19.11.2018
Просмотров: 391
Скачиваний: 4
Лабораторная работа
Тема: Оптимизация функционально-технологических свойств гетерогенной рецептурной смеси методом имитационного моделирования
Цель: Применение функций и возможностей табличного процессора MS Excel 2010 для решения задач стохастического программирования.
Постановка задачи.
Рассмотрим задачу моделирования модельной молочной колбасы высшего сорта: нахождение массовых долей ингредиентов фарша, для которых его качественные характеристики максимально приближаются к опорным, при заданном целевом критерии.
Итак, технологом были заданы следующие опорные (безразмерные) ФТС фарша: влага – 68,00 5,00; жир – 14,00 5,00; белок – 17,00 2,10; зола – 1,00 0,30; водосвязывающая способность – 58,00 7,00; предельное напряжение сдвига (ПНС) – 1600,00 100,00; показатель активной кислотности pH – 6,50 0,50.
Обозначим массовые доли ингредиентов фарша: M1 содержание говядины 1-го сорта; M2 содержание свинины полужирной; M3 содержание мяса птицы механической обвалки; M4 содержание молока сухого цельного; M5 содержание яйца цельного (или крахмала). При этом естественное условие для массовых долей M1 + M2 + M3 + M4 + M5 = 1.
В таблице 21 приведены ФТС Xnl каждого отдельного компонента смеси.
Запишем задачу в матрично - векторном виде
Y* M X Y** (1)
Ф(М)
= С M
max,
М
0,
 ,
,
где опорные свойства заданы векторами
Y* = (63,00; 9,00; 15,00; 0,70; 51,00; 1500,00; 6,00)T;
Y** = (73,00; 19,00; 19,00; 1,30; 6,50; 1700,00; 7,00)T;
C = (230; 90; 215; 20; 75), где С = БЦ – СБ;
M = (M1, …, М5)T – вектор массовых долей ингредиентов фарша;
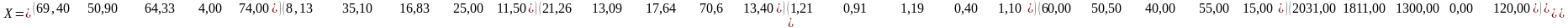 – матрица
ФТС ингредиентов.
– матрица
ФТС ингредиентов.
Таблица 21
Характеристики компонентов смеси
|
Хnl |
l |
||||||
|
Хn1 |
Хn2 |
Хn3 |
Хn4 |
Хn5 |
|||
|
n |
1 |
Влага |
69,40 |
50,90 |
64,33 |
4,00 |
74,00 |
|
2 |
Жир |
8,13 |
35,10 |
16,83 |
25,00 |
11,50 |
|
|
3 |
Белок |
21,26 |
13,09 |
17,64 |
70,60 |
13,40 |
|
|
4 |
Зола |
1,21 |
0,91 |
1,19 |
0,40 |
1,10 |
|
|
5 |
ВСС |
60,00 |
50,50 |
40,00 |
55,00 |
15,00 |
|
|
6 |
ПНС |
2031,00 |
1811,00 |
1300,00 |
0,00 |
120,00 |
|
|
7 |
pH |
6,40 |
6,20 |
6,30 |
5,40 |
6,10 |
|
|
8 |
БЦ |
150,00 |
180,00 |
260,00 |
100,00 |
125,00 |
|
|
9 |
СБ |
80,00 |
90,00 |
45,00 |
80,00 |
50,00 |
|
При моделировании функционально-технологических свойств рецептурных смесей с необходимо учитывать их структурную неоднородность (внутренний фактор) и неопределенности показателей характеристик влаги, жира, белка и т. д.. Ограничения задачи (1) с учетом неопределённости внешних и внутренних факторов примут вид:
Y* M (X + ) Y**, (2)
где = (nl) – матрица помех характеристик смеси.
Степень неполноты исходной информации задачи (2) находит свое отражение в виде закона распределения случайной величины nl , обусловленной как разбросом ФТС ингредиентов, так и структурными факторами, зависящими от параметров технологического процесса.
Методика решения задачи
Используем метод статистического моделирования - метод Монте-Карло, основная идея которого заключается в использовании случайных выборок для получения случайных оценок. Процесс получения случайных выборок предполагает формализацию задачи с учетом соответствующих законов распределений случайных величин. Пусть распределение случайной величины - помех nl описывается равномерным законом распределения. Тогда, алгоритм решения задачи моделирования свойств рецептурной смеси методом имитационного моделирования или методом Монте-Карло следующий:
-
генерируя различные конкретные значения помех nl, получаем i- ое состояние системы, где i=1, 2,…, k;
-
для каждого i-го состояния системы находим решение соответствующей детерминированной задачи линейного программирования, если это возможно;
-
сохраняем полученное решение детерминированной задачи линейного программирования
-
множество решений детерминированных задач Mn = (M1n, M2n,…,МLn), где n = 1, 2,…, N, N ≤ k, используется для оценивания математического ожидания áMñ (см. раздел 1.4);
-
полученные оценки
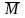 =(
=( ,
,
 ,
…,
,
…,
 )
математического
ожидания áMñ = (áM1ñ, áM2ñ, …, áMLñ)
выбираются в качестве точечной оценки
решения задачи.
)
математического
ожидания áMñ = (áM1ñ, áM2ñ, …, áMLñ)
выбираются в качестве точечной оценки
решения задачи.
Способ решения задачи.
Для решения задачи методом Монте-Карло при помощи электронной таблицы Microsoft Excel выполним следующие действия.
-
Ввод исходных данных.
Введем детерминированные числовые данные (таблица 22).
Таблица 22
Ввод исходных данных
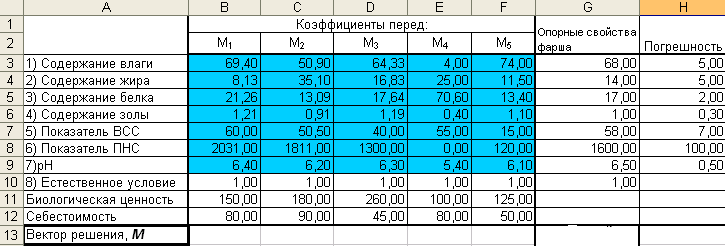
В ячейки I3:I9 введем значения вектора Y*; в ячейки J3:J9 Y**.
2. Генерирование матрицы помех .
Пусть флуктуации помех nl составляют не более 2% от характеристик Xnl ингредиентов. Будем генерировать равномерно распределенные случайные числа nl из интервала, (Xnl 0,01; Xnl + 0,01). В $K$3 запишем 0,01. В B25 = ($K$3* B3 – СЛЧИС()*$K$3* B3*2). Скопируем её в ячейки B25:F31. При каждом нажатии клавиши F9 случайные числа будут генерироваться в ячейках B25:F31.
Чтобы избежать пересчета матрицы помех при каждой итерации инструмента Поиск решения, перепишем ее в ячейки B32:F38, используя программу на VBA.
Для запуска редактора VBA необходимо выполнить команды: пункт меню Разработчик, пиктограмма Visual Basic.
Для добавления нового модуля в рабочую книгу необходимо выполнить команды: Вставка, Модуль (Insert, Module). Новый модуль будет сразу же открыт, и в него можно записать процедуру:
Sub Макрос1()
Range("B25:F31").Select
Selection.Copy
Range("B32").Select
Selection.PasteSpecial Paste:=xlValues, Operation:=xlNone, SkipBlanks:= _False,
Transpose:=False
Application.CutCopyMode = False
Range("B33").Select
End Sub
Для запуска макроса выберем пункт меню Разработчик, пиктограмма Макросы. Появится диалоговое окно Макросы, в котором находится список доступных макросов. Необходимо щелкнуть на имени макроса, который хотим выполнить и на кнопку Выполнить. Для быстрого запуска назначим макрос кнопке, которую поместим на рабочий лист. Входим в пункт меню «Разработчик», выбираем пиктограмму «Вставить», выбираем элемент «Кнопка» из «Элементы ActiveX» см. рис. 18.
Рис. 18.
Двойным щелчком нажимаем на вставленную кнопку и входим в редактор Visual Basic, где виден код метода - обработчика нажатия на вставленную, кнопку см. рис. 19. В поле метода набираем команду call макрос1, где макрос1 – имя ранее созданного макроса.

Рис. 19.
3. Решение детерминированной задачи линейного программирования.
Матрицу коэффициентов X + зададим в ячейках B16:F22.
В B16 = B3 + B33, затем скопируем ее в остальные ячейки диапазона B16:F22.
Решим полученную детерминированную задачу, используя инструмент Поиск решения.

Рис.20. Диалоговое окно Поиск решения
В ячейку G16 введем следующую формулу: =B16* $B$13+ C16* $C13+ D16* $D$13+ E16* $E$13+ F16* $F$13. Скопируем её в ячейки H16:H22.
В G23=B10* $B$13 + C10* $C13 + D10* $D$13 + E10* $E$13+ F10* $F$13.
В G24=(B11-B12)*$B$13+(C11-C12)*$C13+(D11-D12)*$D$12+(E11-E12)* *$E$13+(F11- F12)*$F$13.
Выберем команду меню Данные Поиск решения. Если такая команда недоступна, необходимо её установить, выбрав опцию меню Файл Надстройки Перейти и установив флажок возле пункта Поиск решения в появившемся списке надстроек. Оформим диалоговое окно Поиск решения, как показано на рис. 20.
Нажмем кнопку Параметры. В появившемся диалоговом окне установим следующие переключатели (см. рис. 21).

Рис. 21. Диалоговое окно Параметры поиска решения
Для поиска решения нажмем на кнопку Выполнить. В диалоговом окне Результаты поиска решения установим переключатель в положение Сохранить найденное решение и нажмем кнопку ОК.
Искомые M1; M2; M3; M4; M5 будут находиться в ячейках B13:F13. Опорные (безразмерные) потребительские свойства фарша, рассчитанные машиной, будут находиться в ячейках G16 (влага), G17 (жир), G18 (белок), G19 (зола), G20 (водосвязывающая способность), G21 (предельное напряжение сдвига), G22 (pH), G23 (естественное условие), G24 (целевой критерий).
4. Сохранение решения задачи для последующей обработки.
Сохраним найденные решения при помощи программы, которая будет копировать решение из ячеек B13:F13 Листа1 в ячейки B4:F4, B5:F5 и т.д. Листа2, подсчет числа решенных задач осуществим при помощи функции MsgBox().
Добавим в проект новый модуль. Для этого выполним последовательность команд: Сервис, Макрос, Макросы, Войти. Выберем имя проекта Module1, команды Insert, Module. Появится пустое окно Code. Запишем следующую программу:
Public n, d, As Integer
Sub Макрос2()
For a = 2 To 6
Worksheets("лист2").Cells(4 + d, a) = Worksheets("лист1").Cells(13, a)
Next a
d = d + 1: n = n + 1
MsgBox ("n= " + Str(n))
End Sub
Назначим макросу команду меню: Сохранение решения.
Проведем N экспериментов: Копирование матрицы случайных чисел, Поиск решения, Сохранение решения (если решение найдено) и т.д.
5. Оценивание вектора áMñ = (áM1ñ, áM2ñ, áM3ñ, áM4ñ, áM5ñ) и статистический анализ решения.
Проведем статистический анализ результатов испытаний при помощи инструмента Excel «Описательная статистика», который автоматически вычисляет наиболее широко используемые характеристики распределений случайных величин.
Выберем в строке меню Данные, пиктограмма «Анализ данных», инструмент анализа Описательная статистика. В появившемся диалоговом окне Описательная статистика укажем в соответствующих аргументах: Входной интервал В3: F53; Группирование по столбцам; Метки в первой строке ; Параметры вывода новый рабочий лист; Итоговая статистика ; Уровень надежности 95 %.
После нажатия кнопки ОК новый лист книги будет заполнен вычисленными характеристиками имитационных данных. Эти характеристики (после несложного форматирования) показаны в таблице 23.
Таблица 23
Статистические данные по выборке
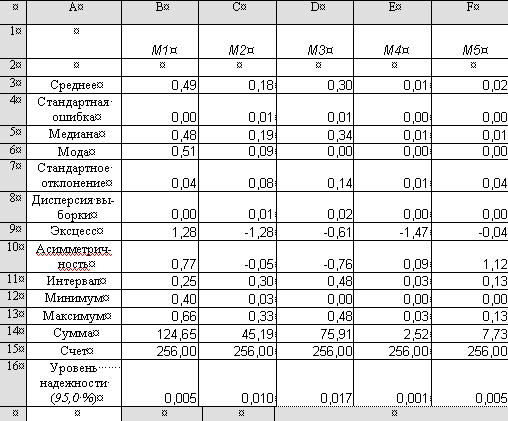
Следует заметить, что коэффициент асимметрии, величину эксцесса, доверительный интервал возможно вычислить с помощью функций СКОС(), ЭКСЦЕСС() и ДОВЕРИТ() мастера функций.
В третьей строке таблицы 23 показаны математические ожидания случайных величин, вычисленных с погрешностями, определенными в четвертой строке.
Медиана значение случайной величины, которое делит площадь под кривой ее распределения пополам. В симметричных распределениях значение медианы равно или достаточно близко к математическому ожиданию.
Мода наиболее вероятное значение случайной величины. Если мода отсутствует, то Excel возвращает сообщение об ошибке (#Н/Д).
Эксцесс (e) характеристика остроконечности (при положительном значении) или пологости (при отрицательном значении) распределения по сравнению с нормальной кривой.
Асимметричность (коэффициент асимметрии или скоса s) характеристика смещения распределения относительно математического ожидания (вправо при положительном значении).
Интервал разность между максимальным и минимальным значениями случайной величины.
Счет число значений в заданном интервале.
Сумма сумма случайных величин в заданном интервале.
Уровень
надежности
величина доверительного интервала для
математического ожидания, соответствующая
заданному уровню надежности (95%). Так,
например, с вероятностью 0,95 оценка
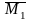 величины
математического ожидания M1
попадает в интервал 0,49
0,005.
величины
математического ожидания M1
попадает в интервал 0,49
0,005.
Вопросы и задания к лабораторной работе
1. Решите задачу, когда помех nl составляют не более 3%, 4,…10% от характеристик Xnl ингредиентов.
-
Решите задачу, когда помехи nl = 0. Сделайте вывод о влиянии различных видов неопределенности ни решение задачи.
-
Постройте гистограмму зависимости решения задачи (полученных массовых долей) от величины помехи nl, %.