Файл: Практикум по измерению электрических и неэлектрических величин.pdf

66

При выполнении задания необходимо: 

а) используя один из известных методов расчета электрических цепей 

(законы Кирхгофа, метод контурных токов, метод узловых потенциалов или 

теорему  об  эквивалентном  генераторе),  вывести  формулы  для  вычисления 

тока в измерительной диагонали I

Г

 и тока, протекающего по преобразовате-

лю I

1

; 

б)  определить  сопротивления  плеч  R

2

, R

3

, R

4

  и  сопротивление  гальва-

нометра R

Г

, а также рассчитать силу тока I

Г

 при различных значениях 

β

 (ре-

комендуется  изменять 

β

  с  шагом 

∆β

=0,1)  и  построить  график  зависимости 

I

Г

=f(

β

); 

в) найти максимальное (I

1  МАКС

) и минимальное (I

1  МИН

) значения силы 

тока, протекающего по резистору R

1

;

г) определить чувствительность схемы для нескольких участков кривой 

I

Г

=f(

β

) и построить график зависимости S=f(

β

); 

д)  вывести  формулу  для  расчета  значения  коэффициента  k

′

,  при кото-

ром  обеспечивается  (при  неизменных  остальных  параметрах)  максимальная 

чувствительность схемы S

МАКС

, и вычислить её значение. 

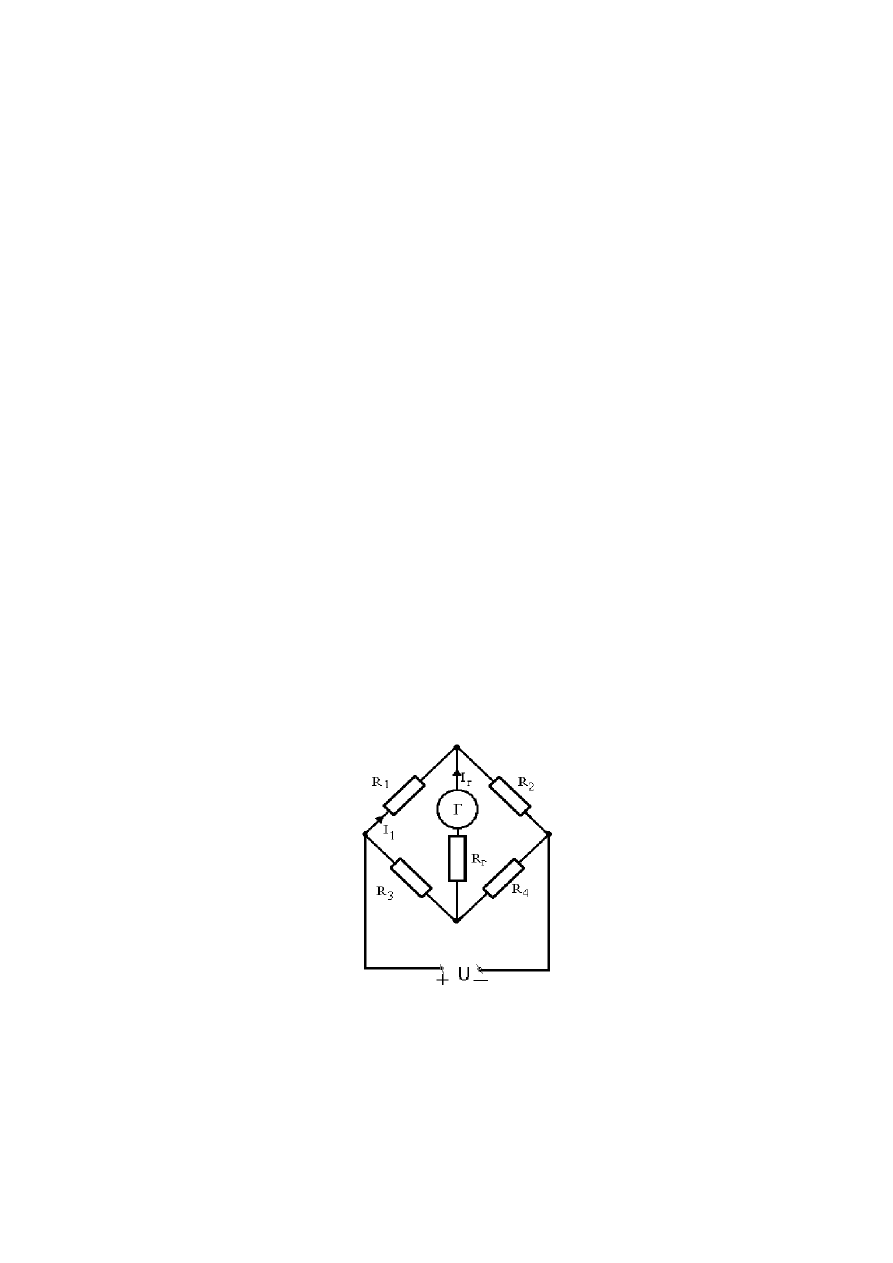
Рис. 3.4. Схема неуравновешенного моста постоянного тока 

Последовательность  расчёта  схемы  изложена  ниже.  Зависимость 

токов I

1

 и I

Г

 от напряжения питания U и сопротивлений резисторов схемы 

имеют вид: 

67

I

1

=U[R

3

(R

2

+R

4

)+R

Г

(R

3

+R

4

)]/M; 

I

Г

=U(R

1

R

4

–R

2

R

3

)/M ,

где 

M=R

Г

(R

1

+R

2

)(R

3

+R

4

)+R

1

R

2

(R

3

+R

4

)+R

3

R

4

(R

1

+R

2

). 

Для удобства дальнейших расчётов многочлен M целесообразно пред-

ставить в виде: 

M=a+bR

1

, 

где 

a=R

2

[R

Г

(R

3

+R

4

)+R

3

R

4

]; 

b=(R

Г

+R

2

)(R

3

+R

4

)+R

3

R

4

 . 

Зная соотношения k, m, n между сопротивлениями, коэффициенты a 

и b можно выразить следующим образом: 

a=km R

1.0

3

 [n(1+k)+km]; 

b=m R

1.0

2

 [(k+n)(1+k)+km]. 

При равновесии мостовой схемы (при I

Г

=0). 

R

1.0

R

4

=R

2

R

3

 . 

Отсюда  неизвестное  сопротивление  R

4

  определяется  по  соотноше-

нию: 

R

4

=R

2

R

3

/R

1.0

=kmR

1.0

 . 

Допустим,  что  задано U=100 В; k=2,5; m=1; n=5 и  известно,  что 

измеряемое сопротивление первого плеча R

1

 изменяется по закону: 

R

l

=R

1.0

(1+

β

), 

где R

1.0

 =50 Ом, а 

β

 может принимать значения от 0 до 1 (при 

β

=0 мост 

находится в равновесии). 

68

В  этом  случае: R

2

=R

4

=125  Ом; R

3

=50  Ом.  Зная  сопротивления  плеч 

моста и R

Г

=250 Ом, можно найти зависимость изменения тока 

∆

I

Г

 от из-

менения измеряемого сопротивления 

∆

R

1

=R

1.0

∆β

. 

Коэффициент 

β

 будем изменять с шагом 

∆β

=0.1.Тогда  

∆

I

Г 

=U

∆

R

1

R

4

/[a+ b(R

1.0

+R

1.0

∆β

)]. 

Результаты расчёта зависимости I

Г

=f(

β

) сведены в табл. 3.8, а гра-

фическое изображение этой нелинейной зависимости приведено на рис. 3.5. 

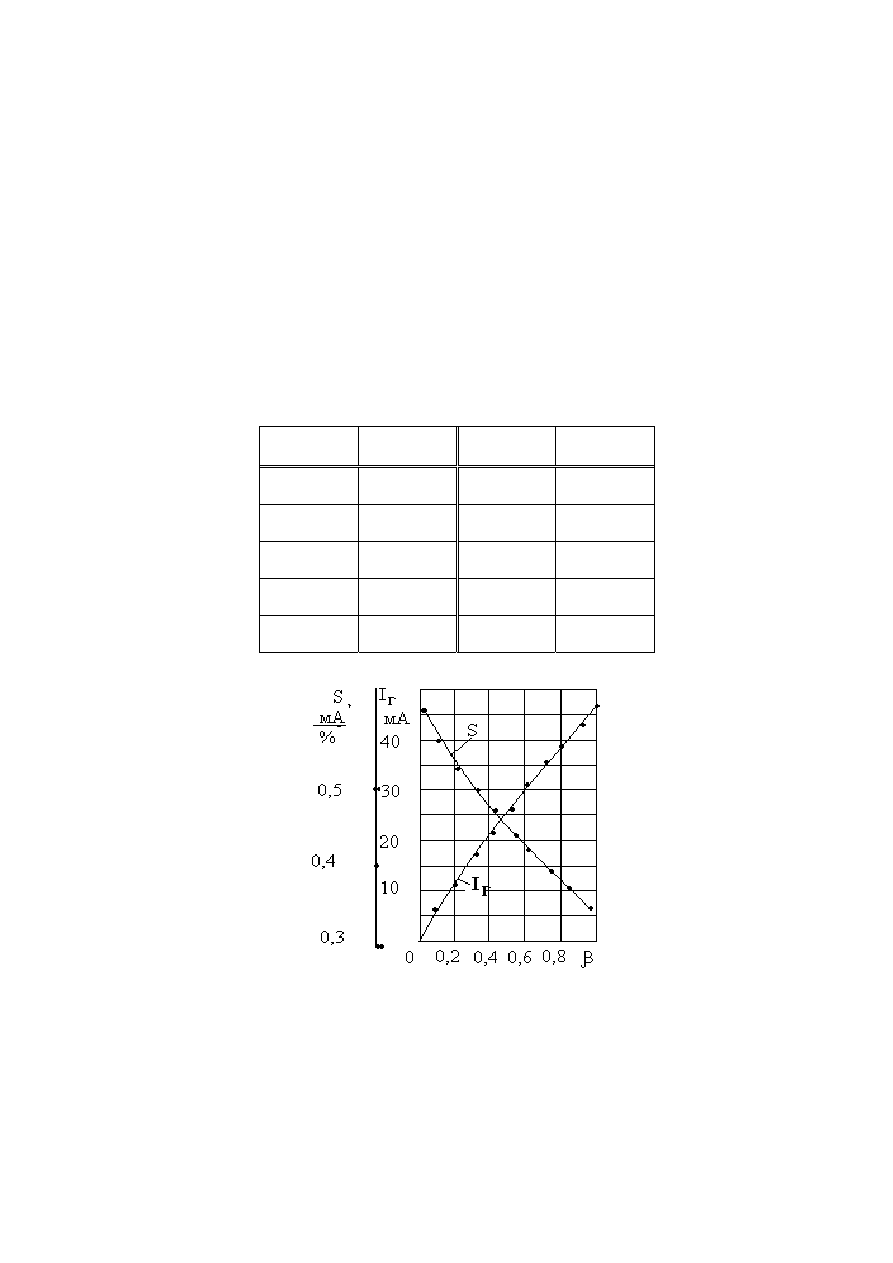
Таблица 3.8 

β

I

г

,мА 

β

I

г

,мА 

0,1 6,13 0,6 31,1 

0,2 11,8 0,7 35,4 

0,3 17,2 0,8 39,3 

0,4 22,2 0,9 43,0 

0,5 26,9 1,0 46,5 

Рис. 3.5. Зависимость тока I

Г

 и чувствительности мостовой схемы от 

β 

По данным табл. 3.8 найдём среднюю относительную чувствитель-

ность  мостовой  схемы  для  каждого i-го  из 10 участков  кривой  I

Г

=f(

β

)  по 

формуле: 

69

S

i

=(I

i

–I

i–1

)/(100

∆β

/

β

МАКС

), 

где I

i 

– значение силы тока, соответствующее 

β

i

. 

При  графическом  построении  зависимости  S

i

=f(

β

i

)  абсциссы  точек 

следует принять равными 

β

I

=

0,5

∆β

. 

Результаты расчёта указанной зависимости для рассматриваемого 

примера приведены в табл. 3.9. 

Таблица 3.9

β

i 

S

i

, мА/%

β

i 

S

i

, мА/%

0,05 0,61 0,55 0,44 

0,15 0,57 0,65 0,42 

0,25 0,53 0,75 0,39 

0,35 0,60 0,85 0,37 

0,45 0,47 0,95 0,35 

Далее найдём значение коэффициента k, при котором обеспечивается 

максимальная  чувствительность  мостовой  схемы  вблизи  её  равновесного 

состояния (при малом отклонении 

∆

I). 

Выразим ток отклонения гальванометра через заданные параметры и 

коэффициенты: 

∆

I

Г

=0.01U

ε

R

1.0

–1

{[n(1+k)+km]+[(k+n)(1+k

–1

)+m](1+

β

)}

–1

 , 

где 

ε

 – относительное изменение сопротивления преобразователя, т.е. 

ε

=100

∆

R

1

/R

1.0

, % . 

Отсюда 

S=

∆

I

Г 

/

ε

=0.01U[R

1.0 

f(k,n,m,

β

)]

–1

. 

70

Максимальная чувствительность S

МАКС

 будет при минимуме функции 

f(k,n,m,

β

). При заданных n, m и 

β

 минимум этой функции обеспечивается, ко-

гда 

k

′

={[n(1+

β

)](1+n+m+

β

)

–1

}

0.5

. 

Для  рассматриваемого  примера,  задавая  небольшое  отклонение 

∆

R

1 

(например, 

β

=0,1),  получим  k

′

=0,88.  В  этом  случае  максимальная  чувстви-

тельность S

МАКС

=1,07 мА/%. 

Завершая  расчёт,  определим  изменение  тока,  протекающего  по  со-

противлению преобразователя при изменении R

1

 от R

1.0

 доR

1.0

+

∆

R

1

. 

Так как 

I

1 МАКС

=U{R

2

1.0

m[k(1+n+m)+n]}/(a+bR

1.0

); 

I

1 МИН

=U{R

2

1.0 

m[k(1+n+m)+n]}/[a+bR

1.0

(1+

β

МАКС

)], 

то 

∆

I=I

1 МАКС

–I

1 МИН

. 

Для рассматриваемого примера I

1 макс

=0,57 А,  I

1 мин

=0.42 A, т.е  

∆

I=I

1 макс

–I

1 мин

=0.15 A. 

Результаты расчёта примера сведены в табл. 3.10. 

Таблица 3.10 

Сопротивление, Ом 

k

′

S

МАКС 

Сила тока, А 

R

1МИН 

R

1МАКС 

R

2 

R

3 

R

4 

R

Г 

мА /% 

I

1 МАКС 

I

1 МИН 

50 

100  125 50 125 250 0,88 

1,07 

0,57 

0,42 

Ответы по всем вариантам задачи даны в табл. 3.11. 

Значения тока I

Г

 (при 

β

=0,5) и S (при 

β

=0,05) приведены для контроля 

правильности расчёта зависимостей I

Г

=f(

β

) и S=f(

β

), соответственно.