ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 6250
Скачиваний: 13

6
контрольных работ. Для этого в пособии представлены образцы
выполнения контрольных задач и тестовых вопросов.
Перед каждой темой приведены краткие сведения из [3],
необходимые для выполнения контрольных заданий.
Для самопроверки, а также для подготовки к устному экза-
мену в конце пособия дан список контрольных (экзаменацион-
ных) вопросов. По каждому вопросу в этом списке указано, на
каких страницах книги [3] находятся ответы.
Пособие можно использовать не только при дистанцион-
ной технологии, но и в очной форме обучения, предлагая сту-
дентам те же тестовые задания и контрольные работы. Очники
при их выполнении могут обойтись без книги [3], если на лек-
ционных занятиях теоретический курс излагается в полном объ-
еме. Если же в очной системе предусматривается частичное ос-
воение материала самостоятельно, то следует обратиться к по-
собию [3], особенно в тех случаях, когда экзаменационные би-
леты составляются из приведенных в нем вопросов.
Данное пособие имеет ту же структуру, что и [3]. В нем
принята нумерация рисунков, формул и таблиц в пределах каж-
дой из пяти вышеперечисленных тем.
Список литературы содержит шесть названий. При необхо-
димости ознакомиться с полным списком литературных источ-
ников, составивших основу пособия, следует обратиться к пуб-
ликациям [1—3], где приведена большая часть источников, ис-
пользованных автором во время работы над учебными пособия-
ми по дискретной математике.
Автор

7
óÄëíú 1
íÖéêàü åçéÜÖëíÇ
1 Ç‚Ó‰Ì˚ Á‡Ï˜‡ÌËfl
По теории множеств курса дискретной математики для кон-
троля предусмотрено две задачи. Одна из них — тест с одно-
значным ответом в виде последовательности десятичных цифр.
Эти цифры необходимо упорядочить по возрастанию и набирать
на компьютерной клавиатуре, начиная с наименьшей из них.
Другая — задача, решение которой необходимо представить в
письменном виде и передать преподавателю.
Для успешного выполнения заданий рекомендуется изучить
содержание нижеприведенных подразделов.
2 íÂÒÚ˚ ÔÓ ÚÂÏ ‹ 1: «éÔÂð‡ˆËË Ì‡‰
ÏÌÓÊÂÒÚ‚‡ÏË»
Выполнение тестового задания проиллюстрируем двумя
примерами с решениями и тремя примерами без решений, но с
ответами.
Пример 1. Из каких элементов состоит множество
P
A
B
A
B
D
A
B
D
C
D
= ∩
∪
∩ ∩
∪
∩ ∩
∪
∩
?
при условии, что
А = {0, 1, 2, 4, 5, 8}; В = {1, 2, 3, 4, 7, 9};
С = {2, 3, 4, 5, 6, 9}; D = {0, 1, 3, 4, 5, 6, 7}.
I
= {0, 1, 2, …, 9}.
Решение. Множества A, B, C, D заданы. Однако кроме них
в формуле P содержатся множества , , ,
A B C D
, т.е. дополнения
множеств A, B, C, D. Найдем их:
A
= {3, 6, 7, 9};
B
= {0, 5, 6, 8};
C
= {0, 1, 7, 8};
D
= {2, 8, 9}.
Выражение P записано в виде объединения четырех состав-
ляющих, каждая из которых представлена пересечением мно-
жеств. Находим элементы первой составляющей A B
∩ :

8
A
B
∩ = {3, 6, 7, 9} ∩ {1, 2, 3, 4, 7, 9} = {3, 7, 9}.
Вторая составляющая есть пересечение трех множеств:
A
B
D
∩ ∩
= {0, 1, 2, 4, 5, 8} ∩ {1, 2, 3, 4, 7, 9} ∩ {2, 8, 9} = {2}.
Третья составляющая также является пересечением трех
множеств:
A
B
D
∩ ∩
=
= {0, 1, 2, 4, 5, 8} ∩ {0, 5, 6, 8} ∩ {0, 1, 3, 4, 5, 6, 7} = {0, 5}.
Наконец находим элементы множества
:
C
D
∩
C
D
∩
= {0, 1, 7, 8} ∩ {0, 1, 3, 4, 5, 6, 7} = {0, 1, 7}.
Объединим элементы всех четырех пересечений:
P = {3, 7, 9} ∪ {2} ∪ {0, 5} ∪ {0, 1, 7} = {0, 1, 2, 3, 5, 7, 9}.
Ответ: P = {0, 1, 2, 3, 5, 7, 9}.
При компьютерном тестировании в качестве ответа набира-
ем упорядоченную по возрастанию последовательность деся-
тичных цифр 0123579 без каких-либо разделительных знаков.
Пример 2. Найдите элементы множества
Q
A
B
C
A
D
B
D
= ∩ ∩
∪
∩
∪
∩
при условии, что
А = {0, 1, 5};
В = {0, 1, 2, 3};
С = {2, 3, 4, 5};
D = {1, 3, 4, 5, 7, 8}.
I
= {0, 1, 2, …, 9}.
Решение. В заданном выражении необходимо найти до-
полнения только для двух множеств:
A
= {2, 3, 4, 6, 7, 8, 9}; B = {4, 5, 6, 7, 8, 9}.
Множество Q представляет собой объединение трех состав-
ляющих, каждая из которых есть пересечение заданных мно-
жеств.
Находим элементы множества A B C
∩ ∩ :
A
B
C
∩ ∩ = {0, 1, 5} ∩ {0, 1, 2, 3} ∩ {2, 3, 4, 5} = Ø.
Аналогично находим элементы множеств A D
∩
и B
D
∩
:
A
D
∩
= {2, 3, 4, 6, 7, 8, 9} ∩ {1, 3, 4, 5, 7, 8} = {3, 4, 7, 8}.
B
D
∩
= {4, 5, 6, 7, 8, 9} ∩ {1, 3, 4, 5, 7, 8} = {4, 5, 7, 8}.
Объединив эти результаты, получаем:
Q = Ø ∪ {3, 4, 7, 8} ∪ {4, 5, 7, 8} = {3, 4, 5, 7, 8}.

9
Пример 3. Найдите элементы множества
Q
A
B
D
A
B
C
C
D
= ∩ ∩
∪
∩ ∩
∪
∩
при условии, что
А = {1, 2, 4};
В = {1, 2, 3, 5, 6};
С = {2, 3, 4, 5, 6, 9};
D = {1, 3, 4, 6, 9}.
I
= {0, 1, 2, …, 9}.
Действуя как и в двух предыдущих случаях, получаем:
Q = {1, 3, 4, 5, 6, 9}.
Пример 4. Найдите элементы множества
Q
A
C
D
B
D
B
C
D
= ∩ ∩
∪
∩
∪
∩ ∩
при условии, что
А = {3, 5, 8};
В = {0, 3, 6, 8};
С = {0, 3, 7, 8, 9};
D = {0, 3, 5, 8, 9}.
I
= {0, 1, 2, …, 9}.
Ответ: Q = {0, 3, 5, 7, 8}.
Пример 5. Найдите элементы множества
Q
A
C
A
B
D
B
C
D
= ∩
∪
∩ ∩
∪
∩ ∩
при условии, что
А = {1, 2, 3};
В = {1, 2, 4, 9};
С = {5, 7};
D = {2, 3, 4, 6, 7, 9}.
I
= {0, 1, 2, …, 9}.
Ответ: Q = {4, 9}.
3 ᇉ‡˜Ë ËÁ ÔËÒ¸ÏÂÌÌÓÈ ÍÓÌÚðÓθÌÓÈ ð‡·ÓÚ˚.
íÂχ 1: «íÂÓðËfl ÏÌÓÊÂÒÚ‚»
Эта работа выполняется письменно, так как ответом к зада-
че является рисунок, компьютерная проверка правильности ко-
торого в высшей степени проблематична (хотя в принципе и
возможна). Выполнение работы проиллюстрируем на несколь-
ких примерах.
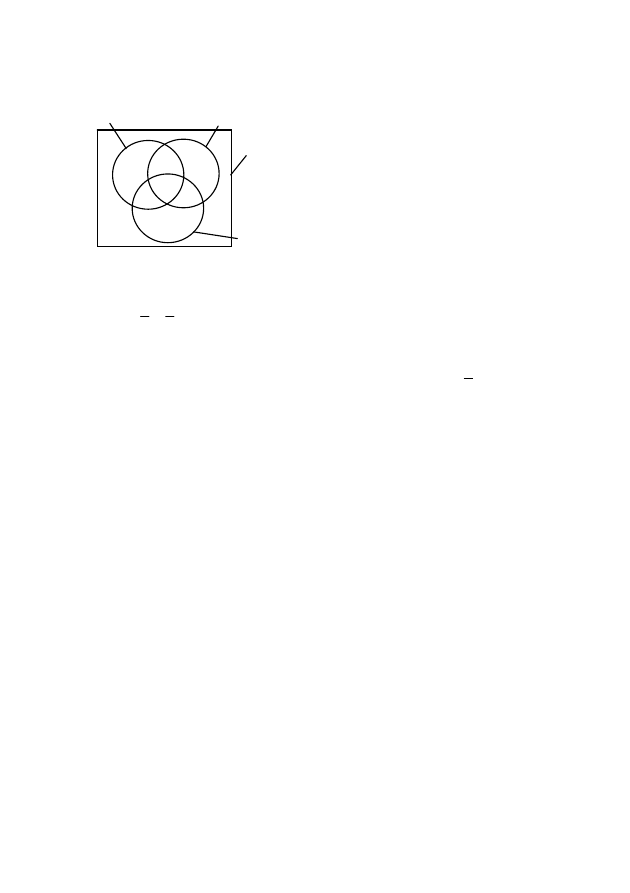
Пример 1. Построить диаграмму Венна для следующих
множеств:
А = {1, 5, 7};
В = {1, 2, 3, 7, 9};
С = {0, 6, 7, 9};
I = {0, 1, 2, …, 9}.
10
Решение. Задано три множест-
ва: A, B и C. В соответствии с этим
на диаграмме Венна изображаем
три пересекающихся круга. Уни-
версальное множество состоит из
всех десятичных цифр. Для каждой
из них найдем место на диаграмме
Венна.
Начинаем с цифры 0. Ее нет в
множестве A и нет в множестве B.
Она содержится только в множестве
C. Это значит, что место цифры 0 находится на пересечении об-
ластей ,
A
B и C (рис. 1).
Цифра 1 является элементом множеств A и B, но не входит
в множество C. Следовательно, цифру 1 записываем в область,
образованную пересечением кругов A, B и областью C .
Цифры 2 и 3 входят только в множество B. Записываем их в
область B, но вне кругов A и C.
Цифр 4 и 8 нет ни в одном из множеств A, B и C. Это зна-
чит, что они находятся вне всех трех кругов.
Цифра 5 является элементом только множества A. Записы-
ваем ее в круг A, но не в области пересечения кругов B и C.
Цифра 6 (как и цифра 0) входит только в множество C. За-
писываем ее в круг C, но вне кругов A и B.
Цифра 7 входит в каждое из множеств. Следовательно, ее
место на пересечении всех трех кругов.
Цифра 9 является элементом множеств B и C, но не являет-
ся элементом множества A. Записываем ее в общую область
кругов B и C, но не в области A.
Таким образом, ответом к данной задаче является диаграм-
ма Венна, изображенная на рис. 1. Заметим, что если при запол-
нении диаграммы не было допущено ни одной ошибки, то за-
данные множества должны совпадать с соответствующими
множествами, обозначенными кругами на диаграмме Венна.
Например, внутри круга A записаны цифры 1, 5 и 7. Из этих же
элементов состоит и заданное множество А = {1, 5, 7}. Внутри
круга B записаны цифры 1, 2, 3, 7, 9. Они же образуют и задан-
1
7
2
3
4
5
0
9
0
8
6
A
B
C
I
Рис. 1