ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 6251
Скачиваний: 13
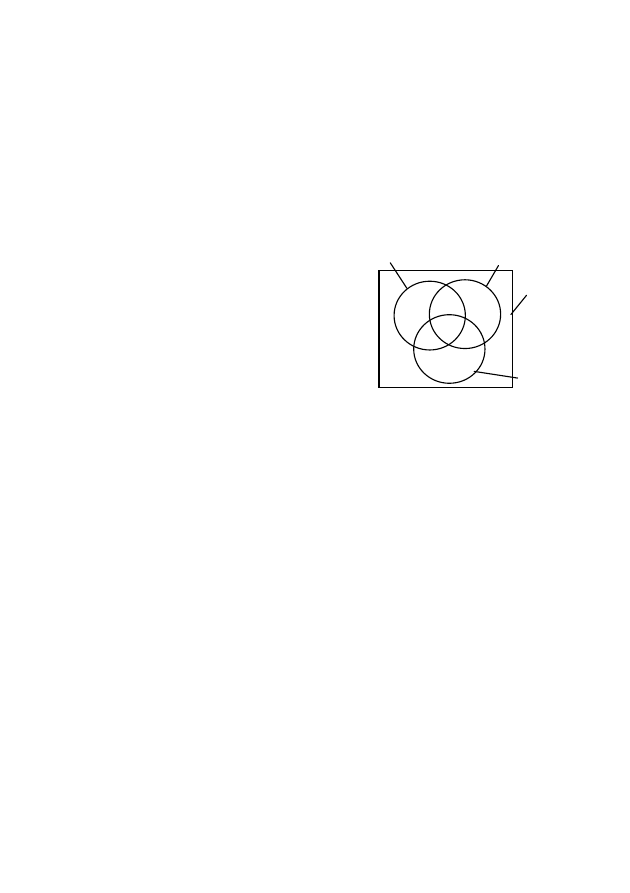
11
ное множество B. В круге C находятся цифры 0, 6, 7, 9. Из этих
же цифр состоит и заданное множество C.
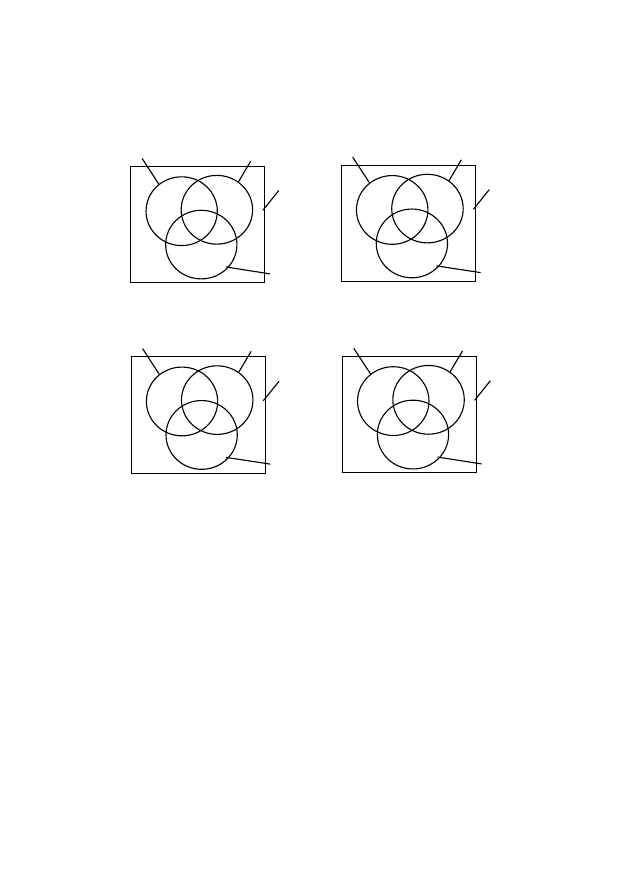
Пример 2. Построить диаграмму Венна для множеств:
А = {0, 4, 9};
В = {0, 1, 2, 3, 4, 7};
С = {0, 5, 6, 7};
I = {0, 1, 2, …, 9}.
Решение. Как и в предыдущем случае, заполняем диаграм-
му, начиная с элемента 0. Этот элемент входит во все множества
A, B и C. Следовательно, цифру 0
ставим в области, где пересекаются
все три круга (рис. 2).
Три цифры 1, 2 и 3 входят в
множество B, но не являются эле-
ментами множеств A и C. Поэтому
внутри круга B, но вне кругов A и C
записываем цифры 1, 2, 3.
Цифру 4 ставим в области пере-
сечения кругов A и B, но вне круга
C, так как цифра 4 принадлежит
множествам A и B и не принадлежит множеству C.
Цифры 5 и 6 располагаем внутри круга C, но снаружи кру-
гов A и B.
Цифры 7 и 8 входят в универсальное множество, но отсут-
ствуют в множествах A, B и C, т.е. не входят ни в одно из этих
множеств. Поэтому цифры 7 и 8 записываем внутри прямо-
угольника вне всех трех кругов.
Осталась цифра 9. Это элемент только множества A. Соот-
ветственно записываем ее в область круга A, но снаружи обоих
кругов B и С.
Таким образом, диаграмма, изображенная на рис. 2, являет-
ся ответом к примеру 2.
Пример 3. Построить диаграмму Венна для множеств:
А = {3, 6, 7};
В = {4, 5, 6, 7};
С = {7, 8, 9};
I = {0, 1, 2, …, 9}.
Ответом является диаграмма, изображенная на рис. 3.
Пример 4. Построить диаграмму Венна для множеств:
А = {0, 1, 5, 6};
В = {3, 5, 6};
4
0
1
2
7
9
5
7
0
8
6
A
B
C
I
Рис. 2
3
12
С = {6, 8, 9};
I = {0, 1, 2, …, 9}.
Ответом является диаграмма, изображенная на рис. 4.
6
7
4
5
2
3
8
0
9
A
B
C
I
Рис. 3
5
6
3
7
0
8
2
9
A
B
C
I
Рис. 4
1
1
4
7
2
9
1
3
8
0
6
5
A
B
C
I
Рис. 5
9
6
2
7
3
4
1
5
A
B
C
I
Рис. 6
0
4
0
8
Пример 5. Построить диаграмму Венна для множеств:
А = {0, 1, 7};
В = {2, 7, 8};
С = {3, 4, 5, 7, 8};
I = {0, 1, 2, …, 9}.
Ответ: диаграмма, изображенная на рис. 5.
Пример 6. Построить диаграмму Венна для множеств:
А = {3, 6, 9};
В = {2, 6, 9};
С = {4, 5, 6};
I = {0, 1, 2, …, 9}.
Ответ: диаграмма, изображенная на рис. 6.
В выполненной контрольной работе должны быть пред-
ставлены условие и ответ в виде заполненной диаграммы Венна
так, как это показано в предыдущих примерах.

13
óÄëíú 2
åÄíÖåÄíàóÖëäÄü ãéÉàäÄ
1 Ç‚Ó‰Ì˚ Á‡Ï˜‡ÌËfl
Среди всех разделов дискретной математики математиче-
ская логика занимает центральное место, в связи с чем в данном
пособии ей уделено значительно больше внимания по сравне-
нию с другими темами. По этой теме предусмотрено четыре тес-
товых задания и пять контрольных работ.
Тестовые задания просты. Ими определяется, достаточно ли
четко студент представляет содержание главных понятий алгеб-
ры логики: конъюнкции, дизъюнкции и инверсии (т.е. логиче-
ских операций И, ИЛИ, НЕ), суммы по модулю 2, дизъюнктив-
ных и конъюнктивных нормальных форм и форм высших по-
рядков, а также полинома Жегалкина.
Контрольные работы призваны выявить более глубокие
знания из математической логики. Это относится к таким темам,
как минимизация булевых формул ДНФ и КНФ, особенно с уче-
том неопределенных состояний, дифференцирование булевых
функций и преобразование логических выражений, содержащих
операцию импликации.
В нижеприведенных подразделах приведены образцы тес-
товых заданий и контрольных работ и даны их решения. Сту-
денту настоятельно рекомендуется ознакомиться с ними, прежде
чем приступать к тестированию и выполнению контрольных
работ. Это поможет ему не только найти верные решения во
время работы над контрольными задачами, но и правильно их
оформить, ориентируясь на приведенные в пособии образцы.
2 íÂÒÚ˚ ÔÓ Ï‡ÚÂχÚ˘ÂÒÍÓÈ ÎÓ„ËÍÂ
2.1 Тесты по теме № 2: «СДНФ булевых функций»
Функция называется представленной в СДНФ, если одно-
временно выполнены следующие два условия:
а) известны аргументы, от которых зависит функция;
б) функция представлена дизъюнкцией нескольких минтер-
мов, при этом минтерм может быть и один.

14
Рассмотрим четыре примера.
Пример 1. Укажите номера всех функций, представленных
в СДНФ.
1)
( , , , , )
;
f A B C D E
A
B
C
D
E
= + + + +
2)
( , , )
;
f A B C
ABC
=
3)
( , , )
(
) ;
f A B D
AB
AB D
=
+
4)
( , , )
;
f A B C
ABC
ABC
ABC
=
+
+
5)
( , , )
(
)(
)(
);
f A B C
A
B
C A
B
C A
B
C
=
+ +
+ +
+ +
6)
( , , , )
(
)(
)(
);
f A B C D
A
B
C
D B
C
D A C
D
=
+ + +
+ +
+ +
7)
.
f
ABC
ABC
ABC
ABC
=
+
+
+
8)
.
f
ABC
=
Решение. Первая функция не является СДНФ, так как не
удовлетворяет второму условию.
Вторая функция состоит из одного минтерма, зависящего от
всех заданных аргументов. Следовательно, одна СДНФ найдена.
Если в третьей функции раскрыть скобки, то получим
СДНФ. Однако при нахождении СДНФ никакие преобразования
не разрешаются. Следовательно, третья функция не является
СДНФ. Она относится к формам высших порядков.
Четвертая функция есть СДНФ, так как она представлена
дизъюнкцией трех минтермов, зависящих от всех заданных ар-
гументов.
Пятая и шестая функции относятся к конъюнктивным фор-
мам и СДНФ не являются
Седьмую функцию можно считать представленной в
СДНФ, если предположить, что она зависит от трех аргументов
A, B, C. Если же предположить, что функция зависит от больше-
го числа аргументов, то к классу СДНФ она не относится. Сле-
довательно, седьмая функция СДНФ не является, так как не вы-
полнено первое условие, т.е. не указаны аргументы, от которых
зависит функция.
Восьмую функцию можно было бы считать представленной
в СДНФ, но так как аргументы, от которых она зависит, не зада-
ны, то к СДНФ ее отнести нет достаточных оснований.
Ответ: 2, 4. (В компьютер необходимо ввести 24.)

15
Пример 2. Укажите номера всех функций, представленных
в СДНФ.
1)
( , , , )
;
f A B C D
ABC
ABC
ABC
=
+
+
2)
( )
;
f A
A
=
3)
( , , , )
;
f A B C D
ABC
BCD
ACD
ABD
=
+
+
+
4)
( , , )
(
)(
)(
);
f A B C
A
B
C A
B
C A
B
C
=
+ +
+ +
+ +
5)
( , , )
;
f A B C
ABC
ABC
ABC
=
+
+
6)
( , , )
;
f A B C
ABC
=
7)
( , , , )
.
f A B C D
AB
CD
AD
=
+
+
Решение. Первая функция внешне походит на СДНФ, но
она не удовлетворяет второму условию (быть дизъюнкцией
минтермов), так как в каждой ее конъюнкции нет переменной D.
Поэтому к СДНФ первая функция не относится.
Вторая функция есть СДНФ. Она зависит от единственного
аргумента A, и этот аргумент указан в ее правой части.
Третья функция представлена не в СДНФ, поскольку не
удовлетворяет второму условию — быть дизъюнкцией минтер-
мов (как и первая функция).
Четвертая функция относится к конъюнктивным формам,
т.е. СДНФ не является.
Пятая и шестая функции представлены в СДНФ.
Седьмая функция СДНФ не является.
Ответ: 2, 5, 6. (В компьютер вводим 256.)
Пример 3. Укажите номера всех функций, представленных
в СДНФ.
1)
( , )
;
f A B
AB
AB
=
+
2)
( , , )
;
f C D E
CDE
=
3)
( , , )
;
f A B C
ABC
ABC
=
+
4)
( , , , )
;
f A B C D
A
B
D
= + +
5)
;
f
ABC
ABC
ABC
ABC
=
+
+
+
6)
( , )
;
f A C
AC
=
7)
( , , , )
.
f A B C D
ABCD
=