Файл: Дискретная мат-ка_Ч.1_УП.pdf

6 

дел,  дающий  представление  о  задачах  и  основных    построениях 
комбинаторного анализа. 

В  конце каждого раздела приведены задачи и упражнения, ко-

торые  необходимо  выполнить  для  закрепления  теоретического  ма-
териала. 

1 

ОСНОВНЫЕ

ПОНЯТИЯ

ТЕОРИИ

МНОЖЕСТВ

1.1 

Основные

определения

Понятие  множества  является  фундаментальным  неопределяе-

мым  понятием.  Интуитивно  под  множеством  понимают  совокуп-
ность  вполне  определенных  различаемых  объектов,  рассматривае-
мых как единое целое. 

Природа  объектов  может  быть  самой  различной.  Так,  можно 

говорить о множестве стульев в комнате, людей, живущих в Томске, 
студентов в группе, о множестве натуральных чисел, букв в алфави-
те,  состояний системы и т.п. Но нельзя, например, говорить о мно-
жестве капель в стакане воды, так как невозможно четко и ясно ука-
зать каждую отдельную каплю, капли неразличимы между собой. 

Отдельные объекты, из которых состоит множество, называют 

его элементами. 

Для  обозначения  конкретных  множеств  принято  использовать 

прописные буквы A, S, X, ... . Для обозначения элементов множества 
используют  строчные  буквы a, s, x, ... . Множество X, элементами 
которого являются x

1

, x

2

, x

3

 , обозначают X = {x

1

, x

2

, x

3

}. Это один 

способ  задания  множества 

−  перечисление  всех  его  элементов.  Он 

удобен  при  рассмотрении  конечных  множеств,  содержащих  не-
большое число элементов. Второй способ задания множества 

− опи-

сательный 

−  состоит  в  том,  что  указывается  характерное  свойство, 

которым  обладают  все элементы множества. Так, если M 

− множе-

ство  студентов  группы,  то  множество X отличников  этой  группы 
записывается в виде 

                          X = {x 

∈ M / x - отличник группы}, 

что читается следующим образом: множество X состоит из элемен-
тов x множества M таких, что x является отличником группы. Мно-
жество  простых  чисел  записывается  как X = {x / x - простое}.  Для 

7 

указания  того,  что  элемент x принадлежит  множеству X, использу-
ется запись   x 

∈ X. Запись x ∉ X означает, что элемент x не принад-

лежит множеству X. 

Множество  называется  конечным,  если  оно  содержит  конеч-

ное  число  элементов,  и  бесконечным,  если  число  его  элементов 
бесконечно.  Множество,  не  содержащее  ни  одного  элемента,  назы-
вается пустым. Пустое множество обозначается 

∅, например: 

                      X ={x 

∈ C / x

2

 - x + 1 = 0} = 

∅, 

где  С - множество  целых    чисел.  Пустое  множество  условно  отно-
сится к конечным множествам. 

Два множества X и Y равны в том и только в том случае, когда 

они состоят из одних и тех же элементов, т.е. X = Y, если x 

∈ X, то  

x 

∈ Y и если y ∈ Y, то y ∈ X. 

Множество X является  подмножеством  множества Y, если 

любой  элемент множества X принадлежит множеству Y. Этот  факт 
записывается как X 

⊂ Y. 

Последовательность  из n элементов  множества  называется               

n-строчкой  или  кортежем.  В n-строчке  каждый  элемент  занимает 
определенное место, тогда как во множестве порядок расположения 
элементов роли не играет. 

Для сокращения записи в теории множеств используются неко-

торые логические символы. Это кванторы общности 

∀ и существо-

вания 

∃, а также символы следствия (импликации) ⇒ и логической  

эквивалентности 

⇔. Смысл этих обозначений следующий: 

∀ - «любой», «каждый», «для всех»; 
∃ - «существует», «найдется», «хотя бы один»; 
⇒ - «влечет», «имеет следствием»; 
⇔ - «тогда и только тогда», «необходимо и достаточно». 
Использование  логических  символов,  например, для определе-

ния подмножества, которое может быть сформулировано в виде: для 
любого x утверждение «x принадлежит X» влечет  за  собой  утвер-
ждение «x принадлежит Y», приводит к записи: 

∀x [x ∈ X ⇒ x ∈ Y]. 

Запись X 

⊂ Y и Y ⊂ X ⇔ X = Y означает: для того, чтобы X 

было равно Y необходимо и достаточно, чтобы X 

⊂ Y и Y ⊂ X. 

8 

1.2 

Операции

над

множествами

Над  множествами  можно  производить  действия,  которые  во 

многом  напоминают  действия  сложения  и  умножения  в  элементар-
ной алгебре. Для графической иллюстрации операций над множест-
вами  будем  использовать  так называемые диаграммы Эйлера, в ко-
торых произвольному множеству X ставится в соответствие множе-
ство точек на плоскости внутри некоторой замкнутой кривой.  

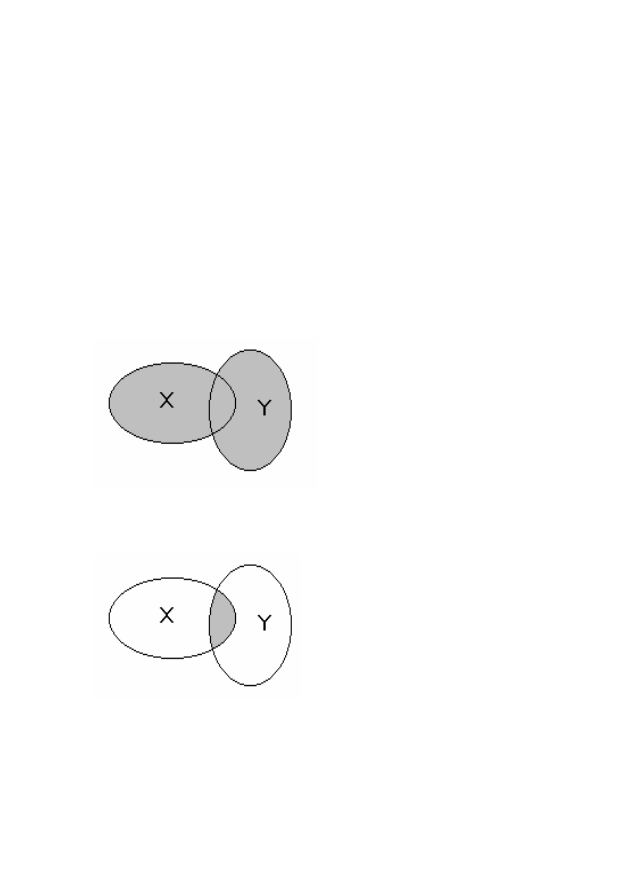
Объединением  (суммой)  множеств X и Y называют  множест-

во, состоящее из всех тех и только тех элементов, которые принад-
лежат хотя бы одному из множеств X, Y (рис.1.1). 

Объединение  двух  множеств  символически  записывают  как           

X 

∪ Y или Y ∪ X. Объединение  множеств  X

i

  (i = 1, 2, ... N) есть 

множество  элементов,  каждый 
из  которых  принадлежит  хотя 
бы одному из множеств X

i

. Со-

ответствующее 

обозначение: 

∪

n

i

i

X

1

=

. 

 
Пересечением  множеств X и Y называют  множество,  состоя-

щее  из  всех  тех  и  только  тех  элементов,  которые  принадлежат  как 

множеству X, так  и  множеству Y 
(рис.1.2). 

 Пересечение  множеств  обо-

значается через X 

∩ Y. Множест-

ва X и Y называют  непересе-
кающимися,  если  они  не  имеют 
общих элементов, т.е. если 
X 

∩ Y = ∅.             

Рис. 1.2 – Пересечение множеств 

Рис. 1.1 – Объединение множеств 

9 

Пересечением множеств X

 i

 (i = 1, 2, ... N) называется множест-

во  элементов,  принадлежащих  всем  X

  i

.  Оно  обозначается  как 

∩

n

i

i

X

1

=

. 

 
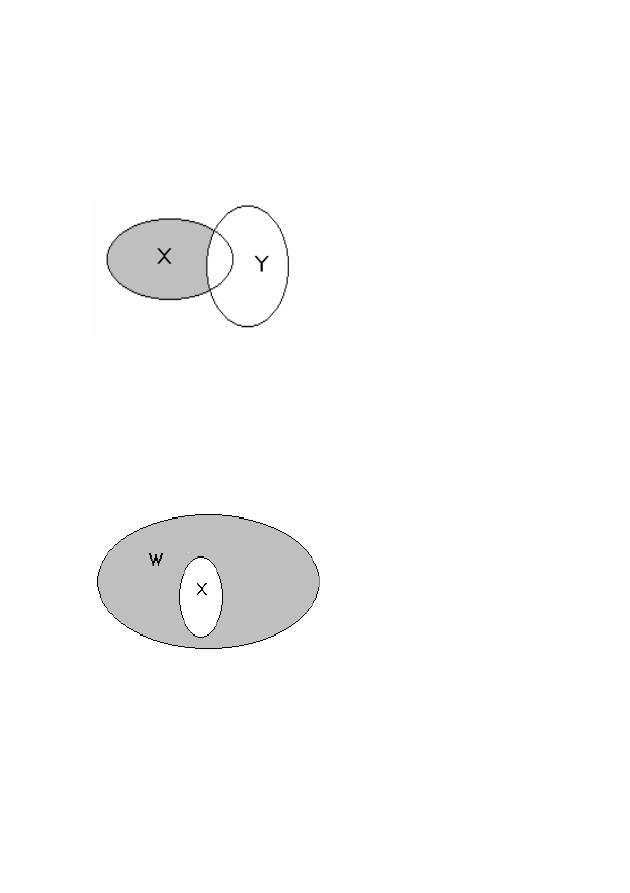
Разностью  множеств X и Y 

называют  множество,  состоящее 
из  всех  тех  элементов,  которые 
принадлежат X и  не  принадлежат 
Y (рис.1.3).  Разность  множеств 
обозначается через X \ Y. 

 
Пример 1. Пусть X – множество  отличников  в  группе, Y – 

множество  студентов,  проживающих  в  общежитии.  Тогда X 

∪ Y – 

множество студентов, которые или учатся на «отлично», или прожи-
вают в общежитии, X 

∩ Y – множество отличников, проживающих в 

общежитии, X \ Y 

− множество отличников, живущих вне общежи-

тия. 

Дополнительным  к 

множеству X по  отноше-
нию  к  множеству W, если 
X 

⊂ W, называется множе-

ство,  состоящее  из  элемен-
тов W, не  принадлежащих 
множеству X. Символиче-
ски  дополнительное  мно-
жество  обозначается  как 
Z

W

(X) (рис.1.4). 

 
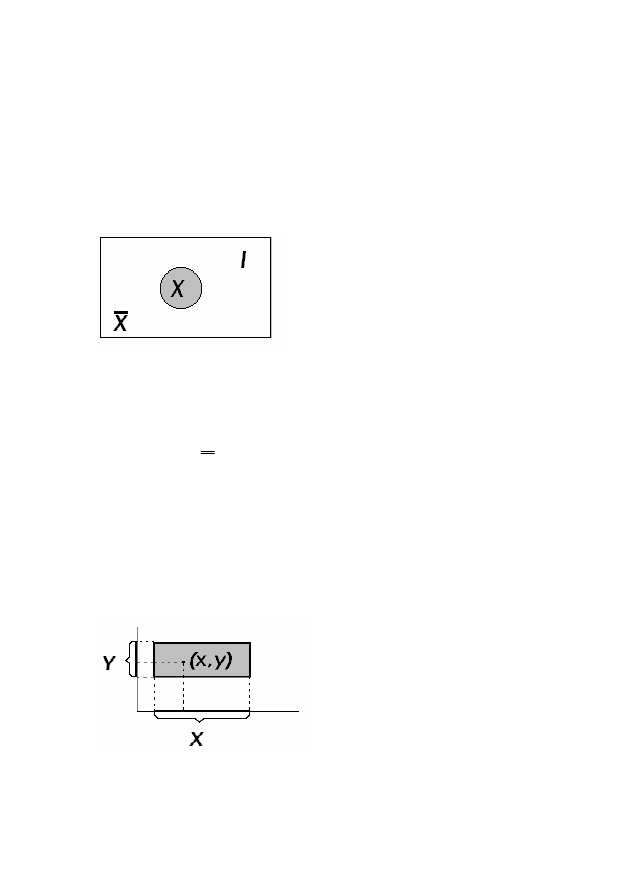
Универсальным множеством называется множество I, для ко-

торого справедливо  соотношение: X 

∩ I = X, означающее, что мно-

жество I содержит  все  элементы  множества X, так  что  любое  мно-
жество X полностью содержится во множестве I. Так, для примера 1 

    Рис. 1.3 – Разность множеств 

Рис. 1.4 – Дополнительное множество 
 

10 

универсальным  множеством  можно  считать  множество  студентов в 
группе. 

Универсальное  множество  удобно  изображать  графически  в 

виде  множества точек прямоугольника. Отдельные области внутри 
этого прямоугольника будут представлять различные подмножества 
универсального множества.  

Множество 

⎯X,  определяемое 

из соотношения

⎯X  = I \ X, называют 

дополнением  множества X (до  уни-
версального  множества I). На  рис 
1.5.  множество

⎯X  представляет  со-

бой не заштрихованную область.  

 
Очевидно выполнение соотношений X 

∩⎯X  = ∅, X  ∪ ⎯X = I, 

из которых следует, что не только

⎯X является дополнением X, но и 

X,  в  свою  очередь,  есть  дополнение 

⎯X. Но дополнение ⎯X есть X. 

Таким образом, 

.

X

X

=

С помощью операции дополнения можно в удобном виде пред-

ставить разность множеств. X \ Y = X 

∩⎯Y. 

Множество упорядоченных пар (x, y), образованных элемента-

ми множеств X и Y, называется декартовым, или прямым, произ-
ведением  множеств X и Y и  обозначается X 

× Y. Таким  образом, 

элементами  декартова  произведения  являются  двухэлементные 
строчки вида (x, y).  

Геометрической  иллюстрацией  декартова  произведения  может 

служить  рис.1.6,  на  котором 
множества    X  и Y изображены 
отрезками  вещественной  оси,  а 
произведение X 

× Y −  заштри-

хованным прямоугольником. Из 
рис.1.6  следует,  что  декартово 
произведение  не  обладает  пере-
местительным свойством                 

                                                                     X 

× Y≠ Y × X.  

Рис. 1.5 – Универсальное  
множество и его дополнение 

Рис. 1.6 – Декартово 
произведение множеств