ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 6739
Скачиваний: 28
11
Пример 2. Пусть X = {x
1 ,
x
2 ,
x
3 ,
x
4
} и Y = {y
1 ,
y
2 ,
y
3
}. Тогда де-
картово произведение X
× Y можно представить табл.1.1.
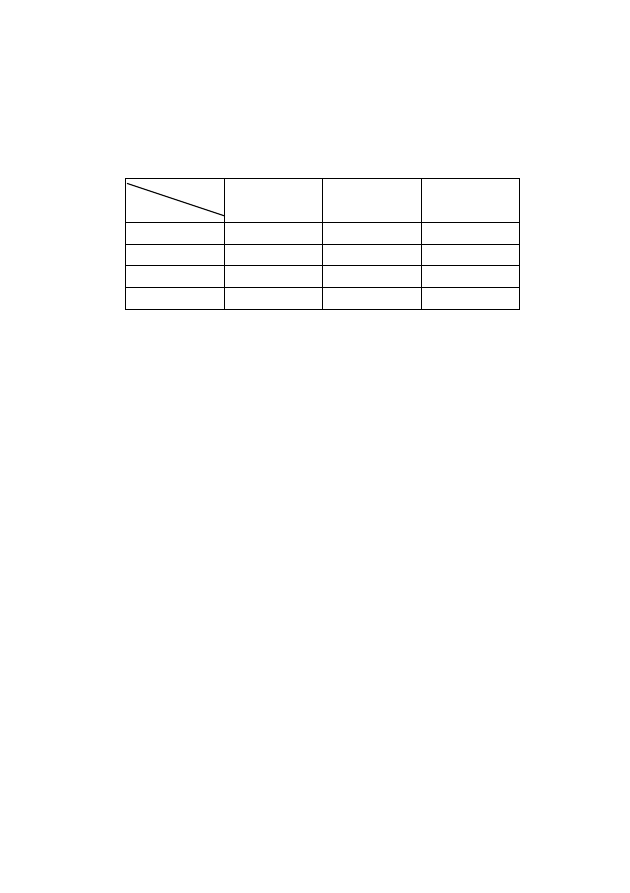
Таблица 1.1 – Пример декартова произведения
Y
X
y
1
у
2
Y
3
x
1
(x
1
, y
1
) (x
1
, y
2
) (x
1
, y
3
)
x
2
(x
2
, y
1
) (x
2
, y
2
) (x
2
, y
3
)
x
3
(x
3
, y
1
) (x
3
, y
2
) (x
3
, y
3
)
x
4
(x
4
, y
1
) (x
4
, y
2
) (x
4
, y
3
)
Декартовым произведением множеств X
1
, X
2
, ... X
n
называют
множество, обозначаемое X
1
× X
2
× ... × X
n
и состоящее из всех тех и
только тех n-строчек, первая компонента которых принадлежит X
1
,
вторая
− X
2
и т.д.
Разбиением множества X называется такое множество мно-
жеств {X
1
, X
2
, ... X
n
}, которое удовлетворяет следующим условиям:
1) X
i
⊂ X, i = 1, ... , n;
2) X
i
≠ ∅, i = 1, ... , n;
3) X
i
∩ X
j
=
∅, при i ≠ j;
4)
.
1
X
X
n
i
i
=
=
∪
Так, например, курсы данного факультета являются разбиением
множества студентов факультета, а группы данного курса
− разбие-
нием множества студентов курса.
Нетрудно показать, что введенные операции над множествами
обладают следующими свойствами:
а) X
∩ Y = Y ∩ X,
X
∪ Y = Y ∪ X;
(коммутативность)
б) (X
∩ Y) ∩ Z = X ∩ (Y ∩ Z),
(X
∪ Y) ∪ Z = X ∪ (Y ∪ Z);
(ассоциативность)
в) X
∩ X = X,
X
∪ X = X;
(идемпотентность)
г) X
∩ (Y ∪ Z) = (X ∩ Y) ∪ (X ∩ Z),
X
∪ (Y ∩ Z) = (X ∪ Y) ∩ (X ∪ Z). (дистрибутивность)

12
1.3
Отношения
на
множествах
Для приложения теории множеств к решению практических за-
дач часто приходится рассматривать множества, между элементами
которых определены те или иные отношения. Так, например, во
множестве офицеров данного полка для некоторых пар элементов
(a, b) справедливо утверждение «Офицер a служит в одной роте с
офицером b», для других пар справедливо утверждение «Офицер a
старше по званию офицера b», для третьих - утверждение «Офицер a
имеет то же звание, что и офицер b». Каждое из этих утверждений
задает некоторое отношение между офицерами a и b (совместной
службы, старшинства, равенства званий). Примерами отношений
могут служить неполные предложения
− предикаты:
... меньше, чем ..., ... делится на ...,
... включено в ..., ... конгруэнтно ... .
В приведенных примерах речь шла об отношениях между эле-
ментами одного и того же множества. Можно говорить и об отно-
шениях (точнее, соответствиях) между элементами различных мно-
жеств - например, утверждение «Офицер a служит в роте b» задает
соответствие между множеством офицеров и множеством рот.
Для определения понятия соответствия используем представ-
ление о множестве упорядоченных пар элементов, троек, n-строчек,
т.е. кортежей.
Бинарным соответствием (отношением) называется всякое
подмножество множества X
× Y. В этом случае говорят, что между
множествами X и Y установлено бинарное соответствие. Этот факт
символически записывается в виде:
x R y , x
∈ X , y ∈ Y,
где R - символ отношения, указывающий конкретное подмножество
множества X
× Y.
Тернарным соответствием (отношением) называется под-
множество множества упорядоченных троек, являющихся элемен-
тами декартова произведения X
× Y × Z.
n - арное соответствие (отношение) определяется как подмно-
жество множества n-строчек, являющихся элементами декартова
произведения
X
1
× X
2
× ... × X
n
.

13
Отметим, что в теории графов в основном рассматриваются
бинарные соответствия, поэтому ограничимся рассмотрением соот-
ветствий только этого типа.
Если множества X и Y в бинарном соответствии совпадают, то
говорят об отношении между элементами множества X. Рассмот-
рим основные свойства отношений.
1.
Отношение R на множестве X называется рефлексивным,
если для любого элемента x
∈ X справедливо x R x или, иначе,
(x, x)
∈ R.
2.
Если условие рефлексивности не выполняется ни для одно-
го элемента x
∈ X, то отношение R называется антирефлексивным.
3.
Отношение R между элементами множества X называется
симметрическим, если для любых элементов x, y
∈ X справедливо
соотношение
x R y
⇒ y R x или (x, y) ∈ R ⇒ (y, x) ∈ R.
4.
Отношение R между элементами множества X называется
антисимметрическим, если для любых элементов x, y
∈ X спра-
ведливо утверждение (x, y)
∈ R ⇒ (y, x) ∉ R. Антисимметрическое
отношение является одновременно и антирефлексивным.
5.
Отношение R между элементами множества X называется
тождественным, если для любых элементов x, y
∈ X справедливо
утверждение: x R y и y R x
⇒ x = y или (x, y) ∈ R и (y, x) ∈ R ⇒
x = y. Антисимметрическое отношение является пересечением тож-
дественного и антирефлексивного отношений.
6.
Отношение R между элементами множества X называется
транзитивным, если для любых элементов x, y, z
∈ X справедливо
x R y, y R z
⇒ x R z или (x, y) ∈ R и (y, z) ∈ R ⇒ (x, z) ∈R.
Примерами транзитивных отношений являются отношения па-
раллельности, равенства, «больше». Отношения перпендикулярно-
сти, неравенства представляют собой нетранзитивные отношения.
7.
Отношение R между элементами множества X обладает
свойством полноты, если для любой пары (x, y) элементов из X все-
гда выполняется одно из двух соотношений: x R y или y R x.
Для каждого отношения R можно определить обратное отно-
шение R
-1
. Краткая запись этого определения выглядит следующим
образом:
∀ R ∃ R
-1
, y R
-1
x
⇔ x R y.

14
Например, для отношения «x является делителем y» обратным
является «y кратно x», для отношения «x больше y» обратно
«y меньше x».
Нулевым называется отношение, которое не выполняется ни
для одной пары элементов множества. Универсальным называется
отношение, которое выполняется для любой пары элементов множе-
ства.
Дополнительным к R отношением
⎯R называется такое отно-
шение, что (x
1
, x
2
)
∈⎯R ⇔ (x
1
, x
2
)
∉ R.
Рассмотрим теперь основные виды отношений.
1.
Отношение R
⊂ X × X между элементами множества X, об-
ладающее свойствами рефлексивности (x R x
∀ x ∈ X), симметрич-
ности (x
1
R x
2
⇒ x
2
R x
1
∀ x
1,
x
2
∈ X) и транзитивности (x
1
R x
2
и
x
2
R x
3
⇒ x
1
R x
3
∀ x
1,
x
2,
x
3
∈ X), называется отношением эквива-
лентности и обозначается x
1
∼ x
2
. Примерами отношения эквива-
лентности являются равенство векторов в евклидовом пространстве,
равенство фигур в евклидовой геометрии. Любое отношение эквива-
лентности, заданное на множестве, разбивает это множество на не-
пересекающиеся подмножества. Так, например, отношение «прожи-
вание в одном городе» на множестве жителей страны разбивает это
множество на непересекающиеся подмножества, количество кото-
рых равно числу городов в стране. Эти подмножества называются
классами эквивалентности. Справедливо и обратное утверждение:
каждое разбиение множества на непересекающиеся подмножества
определяет некоторое отношение эквивалентности.
2.
Отношением квазипорядка на множестве X называется
отношение R
⊂ X × X, обладающее свойствами рефлексивности и
транзитивности. Например, отношение «x
1
≥ x
2
» на множестве веще-
ственных чисел есть отношение квазипорядка. Поэтому данное от-
ношение часто обозначается символом
≥ .
3.
Отношение квазипорядка, обладающее также свойством
тождественности, называется отношением порядка. Оно должно,
таким образом, удовлетворять аксиомам отношения «x
≥ x»: x
1
≥ x
2
и
x
2
≥ x
3
⇒ x
1
≥ x
3
, x
1
≥ x
2
и x
2
≥ x
1
⇒ x
1
= x
2
.
4.
Отношение, обладающее свойствами транзитивности и ан-
тисимметричности, называется отношением строгого порядка.
Это отношение часто обозначают символом >. Оно должно удовле-

15
творять следующим аксиомам: x
1
> x
2
и x
2
> x
3
⇒ x
1
> x
3
, x
1
> x
2
⇒
x
2
> x
1
– невозможно.
5.
Отношением полного порядка называется отношение по-
рядка, обладающее дополнительно еще и свойством полноты. Оно
удовлетворяет аксиомам: x
≥ x; x
1
≥ x
2
и x
2
≥ x
3
⇒ x
1
≥ x
3
;
x
1
≥ x
2
и
x
2
≥ x
1
⇒ x
1
= x
2
;
∀x
1
, x
2
∈ Х ⇒ x
1
≥ x
2
или x
2
≥ x
1
.
6.
Нерефлексивным отношением полного порядка называ-
ется отношение полного порядка, не удовлетворяющее требованию
рефлексивности ни на одном из элементов множества. Оно облада-
ет, следовательно, свойствами транзитивности, антисимметричности
и полноты.
Наглядное представление о перечисленных типах отношений и
их свойствах дает табл. 1.2.
Таблица 1.2. – Виды отношений и их свойства
Отношения
Свойства
Экви-
ва-
лент-
ность
Ква-
зипо-
рядок
Поря-
док
Стро-
гий
поря-
док
Пол-
ный
поря-
док
Нереф-
лексив-
ный
полный
порядок
1.Рефлексивность
* * * *
2.Антирефлексив-
ность
* *
3.Симметричность
*
4.Антисимметрич-
ность
* *
5.Тождественность
* *
6.Транзитивность
* * * * * *
7.Полнота
* *
Кроме того, все рассмотренные отношения и их свойства хо-
рошо иллюстрируются на графах, что мы и покажем несколько
позднее.